
Cryptographic protocols are the backbone of secure communication. Integrating Markov Chains into these systems elevates their ability to predict and mitigate threats through probabilistic modeling.
Let’s explore how this powerful mathematical tool fortifies security.
What Are Markov Chains?
Breaking Down the Basics
A Markov Chain is a mathematical model that predicts the probability of transitioning from one state to another. Unlike traditional systems, it relies solely on the current state, making it a “memoryless” model.
This property is invaluable in dynamic systems where real-time decision-making is crucial. Each state represents a possible situation, and the transitions between them are guided by defined probabilities.
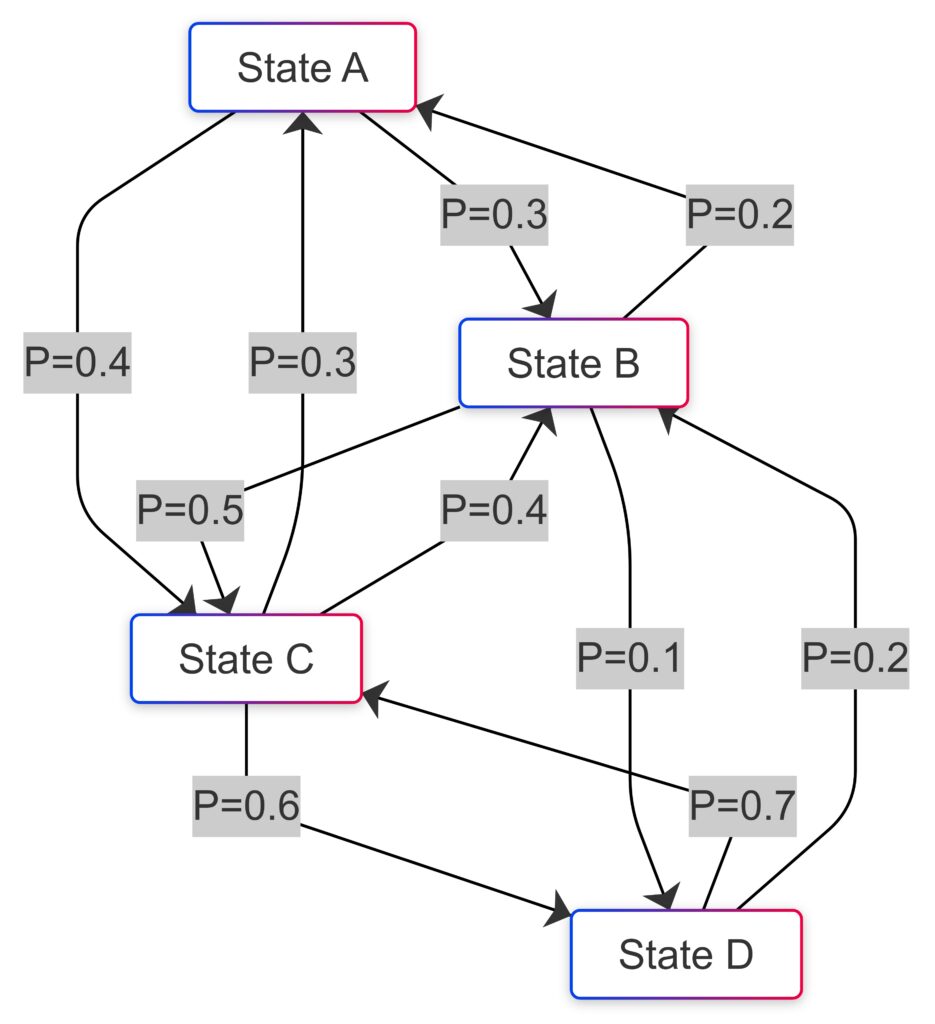
How a Markov Chain transitions between states based on defined probabilities.
Why Markov Chains Work for Cryptography
Cryptography thrives on unpredictability. Markov Chains enhance this by simulating random, yet statistically significant, behaviors. This balance between chaos and order makes them ideal for analyzing and predicting communication patterns or vulnerabilities.
Strengthening Authentication Protocols
The Role of Markov Models in Authentication
Authentication ensures that only the right individuals or devices access sensitive systems. Markov Chains add a probabilistic layer by modeling user behaviors and detecting anomalies.
For example, login patterns often follow predictable trends. A sudden deviation—detected via a Markov Chain—can trigger alerts for potential attacks like credential stuffing or phishing attempts.
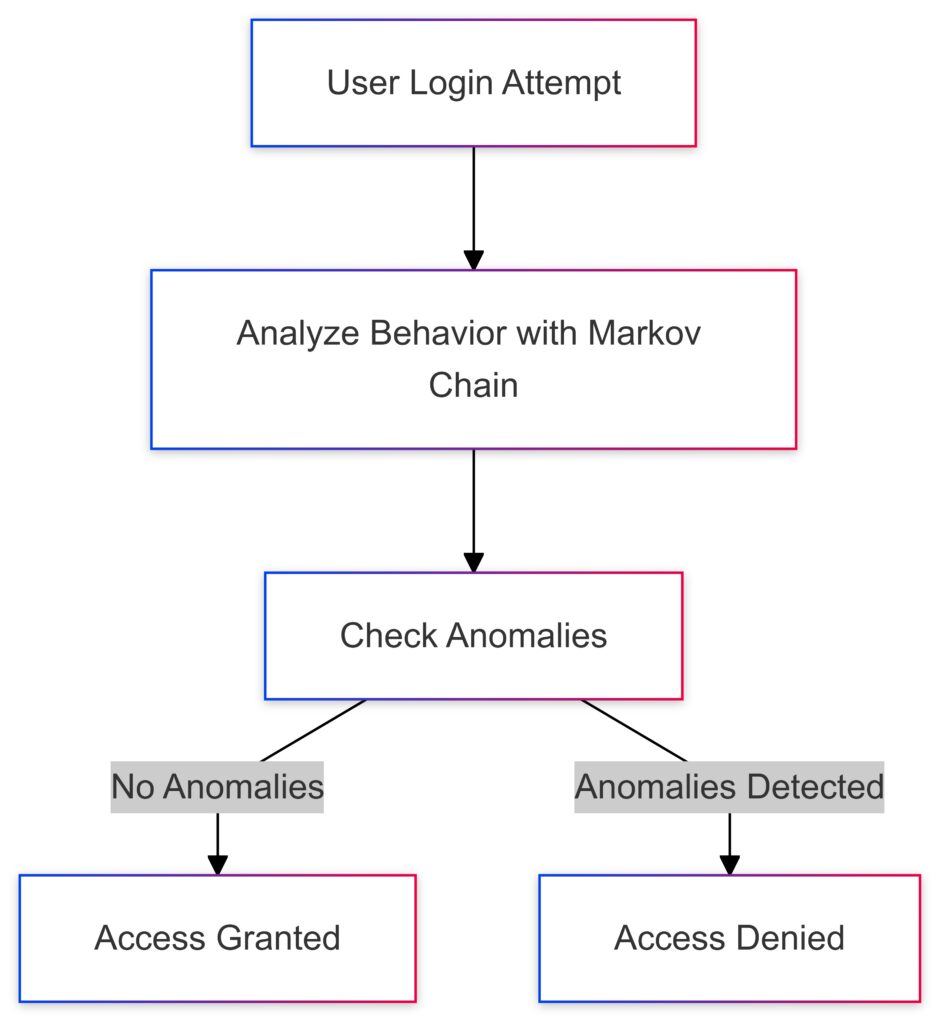
A process flow for incorporating Markov Chains into authentication systems to detect anomalous login behaviors.
Enhancing Key Generation Processes
Markov models also strengthen key generation algorithms. By understanding transition probabilities, they ensure greater randomness and reduced predictability—essential for cryptographic keys resistant to brute-force attacks.

Secure Communication Channels
Markov Chains for Analyzing Traffic
In secure communication, detecting unusual patterns is critical. Markov Chains analyze traffic behaviors and identify deviations that may indicate eavesdropping or man-in-the-middle attacks.
These systems rely on historical data to model expected transitions. Any unexpected states can signal interference or breaches, allowing proactive countermeasures.
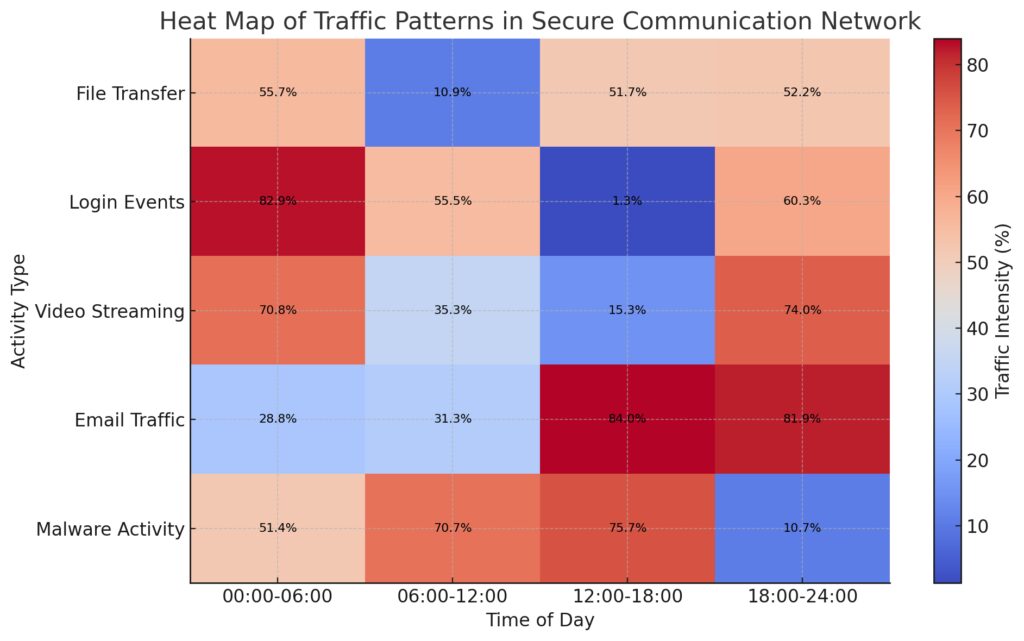
The x-axis represents the time of day, while the y-axis denotes different activity types. The color intensity in each cell reflects the likelihood or intensity of each activity type during the corresponding time period, providing an overview of network traffic dynamics.
Optimizing Protocol Efficiency
Beyond security, Markov Chains optimize protocol performance. By predicting future states, they enable systems to preemptively allocate resources, ensuring seamless encryption and decryption processes.
Detecting Advanced Persistent Threats (APTs)
Identifying Long-Term Patterns
APTs often span months, with attackers lying low to avoid detection. Markov Chains uncover subtle shifts in network behavior over time.
By modeling long-term probabilities, they expose patterns invisible to static systems. This enhances the ability to counteract stealthy, persistent intrusions.
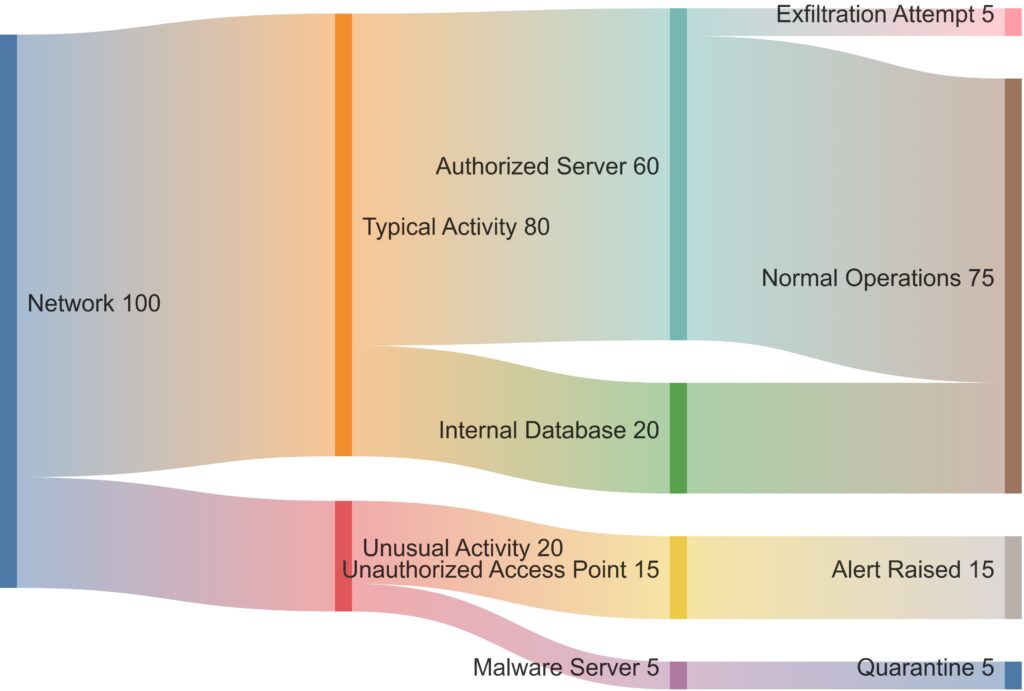
Incorporating Real-Time Adaptability
Threat landscapes evolve rapidly. Markov-based systems adapt in real time, recalculating probabilities with each new state. This flexibility is essential for combating emerging threats.
Ensuring Robustness in Blockchain Security
Markov Chains in Consensus Algorithms
Blockchain relies on consensus mechanisms to validate transactions. By applying Markov Chains, systems can predict network delays or potential disruptions in the consensus process.
This foresight enhances the reliability of decentralized systems, reducing vulnerabilities to 51% attacks or other coordinated exploits.
Improving Smart Contract Audits
Smart contracts execute automatically when conditions are met, but they’re vulnerable to bugs or exploitation. Markov modeling can simulate potential contract behaviors under various conditions, identifying loopholes before deployment.
Modeling Threat Behaviors with Markov Chains
Understanding Attack Vectors Through State Transitions
Cyberattacks often follow a predictable set of steps, from reconnaissance to exploitation. Markov Chains map out these steps as a sequence of states, helping security teams anticipate potential attack paths.
For example, a phishing attack might start with an email, escalate to credential theft, and lead to system infiltration. Markov Chains quantify the probability of each step, enabling proactive defense strategies.
Simulating Adversarial Behaviors
By simulating potential attacker behaviors using probabilistic models, Markov Chains allow systems to predict how an adversary might adapt. This capability is invaluable for penetration testing and red team exercises aimed at hardening systems.
Enhancing Intrusion Detection Systems (IDS)
Improving Detection Accuracy
Traditional IDS often struggle with false positives. Markov Chains improve accuracy by considering sequential data—analyzing how one event leads to another.
For instance, detecting a single failed login attempt isn’t alarming, but a series of them followed by an anomalous IP connection might indicate a brute-force attack. Markov modeling recognizes these patterns in real-time.
Reducing Response Times
With Markov Chains, intrusion detection becomes faster and more efficient. By continuously recalculating probabilities, systems can react swiftly to deviations from normal activity, minimizing potential damage.
Securing IoT Networks with Probabilistic Models

Adapting to Dynamic Environments
The Internet of Things (IoT) introduces unique challenges, as devices often operate in decentralized, ever-changing environments. Markov Chains adapt to these dynamics, modeling state transitions in distributed networks.
For example, they can monitor IoT device behaviors, flagging anomalies like unauthorized firmware updates or unusual data flows.
Fortifying Data Transmission
IoT devices frequently transmit sensitive data over insecure networks. Markov Chains ensure secure communication by predicting vulnerabilities in data routing protocols and enabling adaptive encryption techniques.
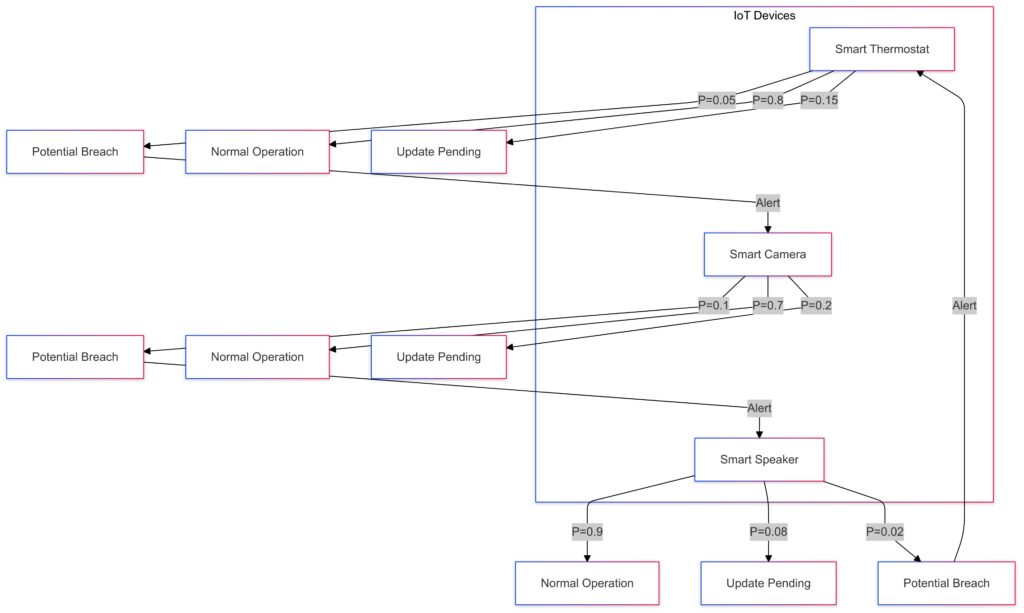
Enhancing Privacy in Cryptographic Systems
Protecting Against Correlation Attacks
Correlation attacks exploit predictable patterns in encrypted data. Markov Chains break these patterns by introducing randomized state transitions, thwarting attempts to infer sensitive information.
For instance, in systems like homomorphic encryption, Markov models randomize data interactions, enhancing both privacy and security.
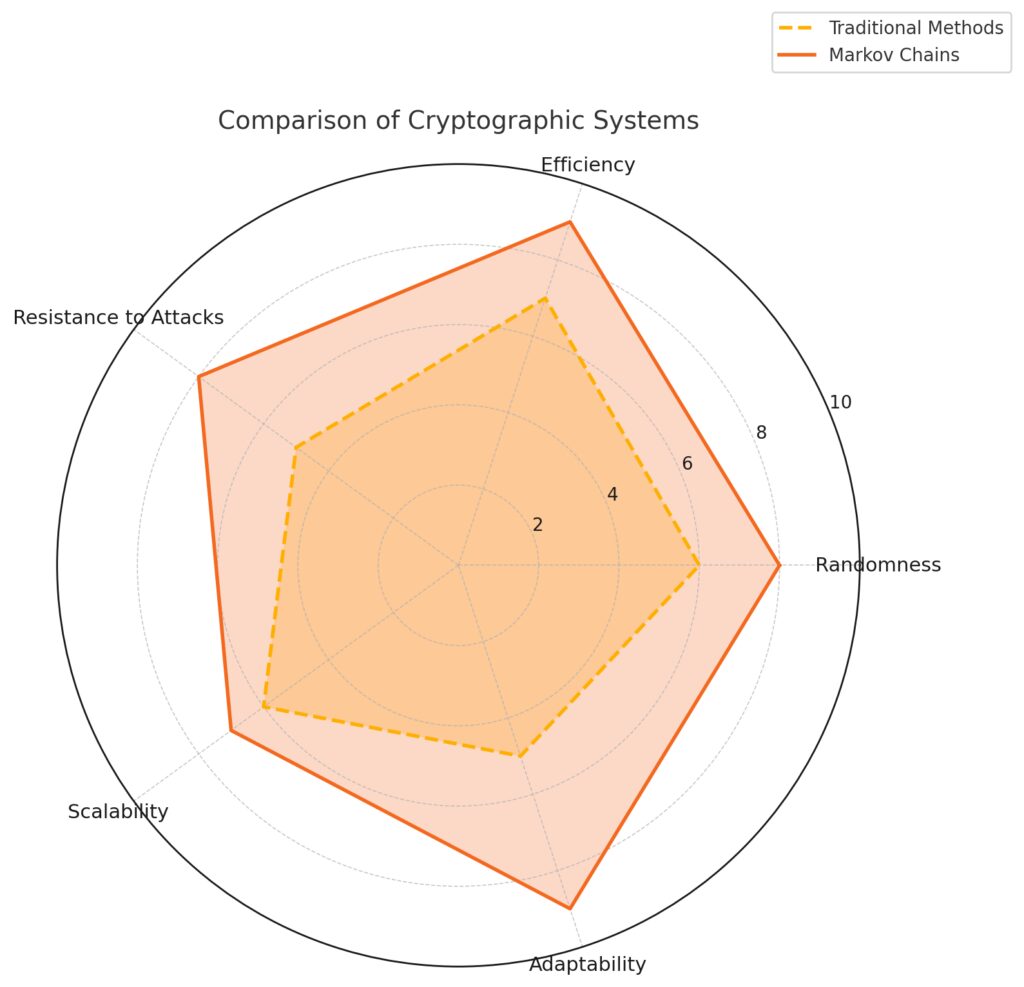
Markov Chains demonstrate superior performance in “Randomness,” “Efficiency,” and “Adaptability,” indicating their strength in generating diverse cryptographic randomness and adapting to various system needs.
Traditional Methods are closer in “Scalability” and “Resistance to Attacks” but lag overall, particularly in adaptability to dynamic environments.
Preserving Anonymity in Decentralized Systems
Anonymity is vital in decentralized networks like Tor or blockchain. Markov Chains model network activity to detect patterns that might compromise user identities, enabling dynamic anonymization strategies.
Challenges in Integrating Markov Chains
Balancing Accuracy with Complexity
While powerful, Markov Chains can become computationally intensive, especially in systems with numerous states and transitions. Simplifying the model without sacrificing accuracy remains a key challenge.
Strategies like aggregating similar states or using higher-order Markov models can strike this balance, ensuring practical implementation.
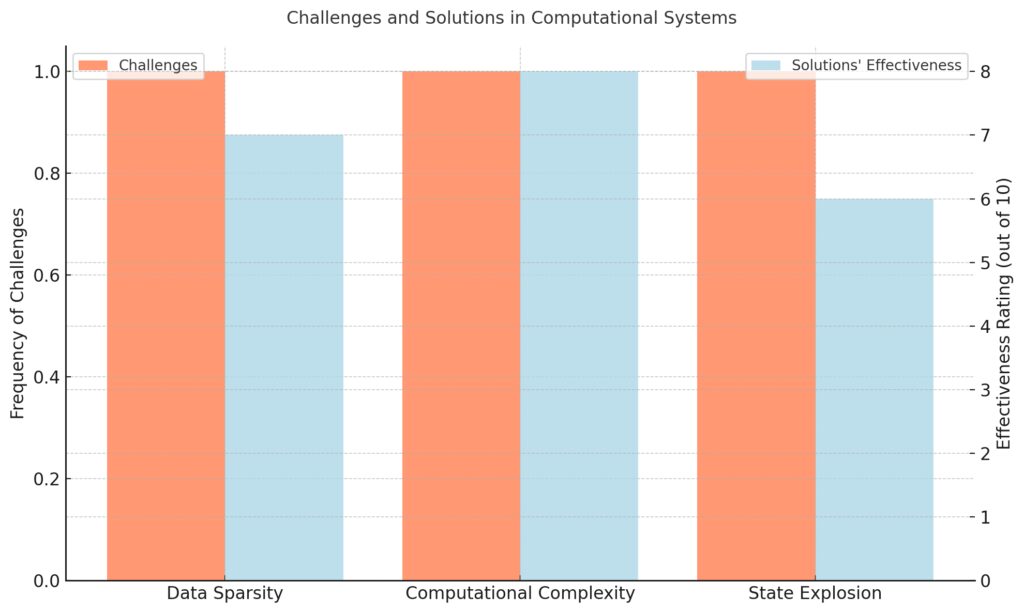
Data Sparsity: A common issue when data availability is insufficient.
Computational Complexity: Arises from the high processing demands of algorithms.
State Explosion: Occurs when system states grow exponentially.
Solutions and Effectiveness:
Data Imputation: Effectiveness rated at 7/10 for addressing data sparsity.
Efficient Algorithms: Highly effective (8/10) in mitigating computational complexity.
State Aggregation: Moderately effective (6/10) in tackling state explosion.
Handling Sparse Data
In some cases, sufficient data to define state transitions accurately may not exist. Markov Chains rely on robust datasets for effectiveness, and sparse or incomplete data can reduce their accuracy.
Techniques like Bayesian inference or reinforcement learning can complement Markov Chains to mitigate this issue, enhancing their predictive power.
Markov Chains in Quantum Cryptography
Enhancing Quantum Key Distribution (QKD)
Quantum key distribution (QKD) relies on principles of quantum mechanics to secure communications. Integrating Markov Chains into QKD enhances its ability to model and mitigate potential threats.
Markov Chains can simulate the probability of various quantum states, identifying patterns that may indicate eavesdropping attempts. This ensures that the generated keys remain truly secure, even in the presence of an adversary.
Strengthening Post-Quantum Cryptographic Algorithms
Post-quantum cryptography aims to resist attacks from quantum computers. Markov Chains can test the robustness of these algorithms by simulating potential attacks, particularly those leveraging probabilistic weaknesses in the encryption methods.
Advanced Use Cases in Blockchain Security
Predicting Blockchain Fork Probabilities
Blockchain forks—intentional or accidental—can disrupt network integrity. Markov Chains model the probability of different forks based on historical and real-time network data.
This allows developers to anticipate and mitigate potential vulnerabilities, such as those that arise during soft forks or contentious hard forks.
Token Economy Simulations
Markov Chains are instrumental in modeling cryptoeconomics—the study of incentives within blockchain networks. By simulating how users interact with tokens under various scenarios, developers can predict market behaviors and design more robust incentive mechanisms.
For example, they can evaluate the likelihood of malicious behaviors like double-spending attacks or selfish mining in specific environments.
Securing Cloud-Based Cryptographic Systems
Dynamic Key Management in Multi-Tenant Environments
Cloud environments host numerous users, each requiring secure access to cryptographic keys. Markov Chains optimize key management systems, ensuring minimal overlap and maximum randomness in key assignments.
This reduces the probability of key collisions and mitigates risks associated with shared infrastructure.
Preventing Insider Threats
Insider threats pose significant risks in cloud settings. Markov Chains analyze access patterns, identifying deviations that may indicate unauthorized activity. By focusing on probabilistic transitions, they differentiate between legitimate anomalies and malicious behavior.
Optimizing Public Key Infrastructure (PKI)
Enhancing Certificate Validation Processes
PKI secures online communication by issuing and validating digital certificates. Markov Chains streamline this process by modeling the likelihood of certificate expiration, revocation events, or malicious certificates entering the system.
By analyzing transition states, they enable proactive alerts for compromised certificates, ensuring consistent security.
Reducing Latency in Secure Connections
When establishing secure connections, latency often becomes a bottleneck. Markov Chains predict bottlenecks in certificate exchange protocols, allowing optimizations that reduce handshake times without compromising security.
AI-Powered Cryptographic Systems
Markov Chains in Neural Cryptography
Neural cryptography combines machine learning and encryption. Markov Chains enhance these systems by providing probabilistic insights into neural network behaviors, identifying potential vulnerabilities during training and deployment.
For instance, they can model the likelihood of a neural network mistakenly decrypting malicious data, enabling preemptive corrections.
Bolstering Secure Machine Learning Models
Markov Chains protect machine learning models from adversarial attacks. By analyzing data transitions within models, they detect and mitigate attacks like poisoning (where malicious data skews training outcomes) or evasion (where adversaries bypass detection).
Key Takeaway: Markov Chains in Cryptographic Protocols
Markov Chains provide a powerful framework for enhancing cryptographic security through probabilistic modeling. By predicting state transitions and analyzing behavior patterns, they:
- Strengthen authentication protocols and key generation by increasing randomness and detecting anomalies.
- Bolster intrusion detection systems by improving accuracy and reducing response times.
- Fortify blockchain and IoT security by simulating vulnerabilities and optimizing dynamic environments.
- Enhance emerging fields like quantum cryptography and neural cryptography, ensuring resilience against advanced threats.
Despite challenges like computational complexity and sparse data, Markov Chains are invaluable in designing adaptive, proactive, and robust cryptographic systems for modern security demands.
FAQs
Can Markov Chains simulate specific attack scenarios?
Yes! Markov Chains are adept at simulating adversarial behaviors. They map out potential attack paths by assigning probabilities to each step, enabling security teams to identify and preempt vulnerabilities.
For example, in a phishing scenario, a Markov model might show that a phishing email leads to a 70% chance of credential theft and a 40% chance of further system infiltration. This insight helps prioritize defense mechanisms.
Are Markov Chains suitable for blockchain security?
Absolutely. Markov Chains are widely used in blockchain systems to improve transaction validation, predict fork probabilities, and analyze user behaviors.
For instance, they can model the likelihood of a blockchain fork due to network delays or malicious activity, helping prevent disruptions in decentralized consensus processes.
How do Markov Chains optimize IoT security?
Markov Chains adapt to the dynamic and decentralized nature of IoT networks. They model device behavior to detect anomalies, such as unauthorized firmware updates or unexpected data transmissions.
For example, an IoT thermostat might show a pattern of usage that deviates from normal heating schedules. A Markov-based system could flag this as a possible compromise and take corrective action, such as isolating the device.
What are the main limitations of Markov Chains in cryptographic systems?
The two key limitations are data sparsity and computational complexity. Sparse datasets make it harder to establish accurate state transition probabilities, while a large number of states can overwhelm computational resources.
In cryptography, these challenges are addressed by simplifying models—grouping similar states—or combining Markov Chains with machine learning techniques like reinforcement learning.
How do Markov Chains contribute to post-quantum cryptography?
Markov Chains play a vital role in testing and improving post-quantum algorithms by simulating probabilistic attack scenarios. They evaluate potential weaknesses in algorithms designed to resist quantum computing power.
For example, lattice-based cryptographic methods can be modeled with Markov Chains to assess their resilience to evolving quantum decryption techniques.
Why are Markov Chains essential for secure communication?
Markov Chains ensure secure communication by modeling traffic patterns, identifying deviations that may indicate eavesdropping, and optimizing encryption processes.
An example is a TLS handshake where the model predicts and mitigates delays, ensuring smoother and safer connections for encrypted web traffic.
How do Markov Chains enhance smart contract security?
Markov Chains simulate potential behaviors of smart contracts, allowing developers to test for vulnerabilities before deployment. By modeling different scenarios, they predict how contracts will behave under varying conditions, such as malicious inputs or network delays.
For instance, in an escrow smart contract, a Markov model might simulate user actions to ensure funds are only released when both parties fulfill the agreed-upon conditions. This reduces risks of manipulation or exploitation.
Can Markov Chains detect advanced persistent threats (APTs)?
Yes, they excel in identifying long-term patterns associated with APTs. APTs often operate stealthily, gradually infiltrating systems to avoid detection. Markov Chains model network behavior over time to uncover subtle deviations from expected transitions.
For example, an APT might involve gradual data exfiltration over several weeks. A Markov-based system can detect these irregularities early by noticing anomalies in data transfer rates or access logs.
How are Markov Chains applied to traffic analysis in cryptography?
Markov Chains monitor and model traffic flows to detect unusual patterns, such as spikes in activity or irregular packet sizes, that may indicate breaches or attacks.
For instance, a denial-of-service (DoS) attack often shows an abrupt increase in request rates. A Markov model would recognize the likelihood of such a state transition and trigger defensive actions, such as blocking offending IP addresses.
What role do Markov Chains play in key exchange protocols?
Markov Chains optimize key exchange protocols by ensuring randomness in key transitions and preventing predictable patterns that attackers could exploit.
For example, in the Diffie-Hellman key exchange, Markov models help test the randomness of generated keys, ensuring their security against cryptanalysis techniques.
Are Markov Chains used in protecting encrypted databases?
Yes, they are effective in securing encrypted databases by analyzing access patterns to detect unauthorized attempts. Markov Chains model normal user behavior, such as query frequency and data access sequences, and flag deviations.
For example, if a user suddenly queries large volumes of sensitive data they don’t typically access, the system can infer a higher probability of a breach and enforce restrictions.
How do Markov Chains prevent side-channel attacks?
Side-channel attacks exploit physical attributes (e.g., power usage, timing) to infer sensitive data. Markov Chains predict these attack probabilities by modeling transitions in observable metrics during encryption processes.
For instance, a Markov model can simulate how power consumption changes when specific encryption keys are used, helping engineers design hardware that masks such variations to thwart attackers.
Can Markov Chains support zero-knowledge proofs?
Yes, Markov Chains assist in optimizing zero-knowledge proof (ZKP) systems by modeling the probabilistic interactions between prover and verifier. This ensures minimal information leakage during the process.
For example, in a ZKP system verifying a user’s age without revealing their exact birth date, Markov Chains can simulate the verification steps to confirm that no unnecessary data is exposed.
How do Markov Chains contribute to adaptive security in real time?
Markov Chains allow systems to dynamically adapt by recalculating probabilities for state transitions based on new data. This real-time adaptability is crucial for responding to emerging threats.
For example, during an active DDoS attack, a Markov model might recognize evolving patterns in traffic and adjust firewall rules instantly, minimizing downtime and maintaining service availability.
Are Markov Chains scalable for large cryptographic systems?
Yes, though scalability can be challenging, Markov Chains are scalable with optimizations. Techniques like state aggregation and higher-order models allow them to handle larger systems effectively.
For example, in a global blockchain network with thousands of nodes, a simplified Markov model might group nodes with similar behaviors, reducing complexity while still providing accurate insights into network security.
Resources
Research Papers and Articles
- “Markov Chains: Theory and Applications” by David Asher Levin, Yuval Peres, and Elizabeth L. Wilmer
A deeper dive into Markov Chains’ theoretical foundations with real-world applications, including cybersecurity.
Access the paper. - “Markov Chains for Cryptographic Key Generation”
Explores how Markov Chains improve randomness in key generation algorithms. Look for this topic in cryptography-focused journals like the Journal of Cryptology. - “A Markov Decision Framework for Intrusion Detection”
Available in journals like IEEE Transactions on Information Forensics and Security. It explains using Markov Chains for proactive defense mechanisms.
Online Courses and Tutorials
- Khan Academy – Probability and Markov Chains
Free, beginner-friendly lessons on probability and Markov processes.
Visit Khan Academy. - Coursera: Applied Cryptography by Stanford University
This course includes modules on mathematical models like Markov Chains for cryptographic applications.
Enroll on Coursera. - MIT OpenCourseWare – Cryptography and Information Security
Offers lectures and assignments to explore Markov processes in the context of cryptographic security.
Explore MIT OCW.
Software and Tools
- MATLAB and Python Libraries
- Use libraries like NumPy and SciPy for Markov Chain modeling in Python.
- MATLAB offers toolboxes specifically for stochastic modeling.
Learn Python for Data Science.
- Markov Chain Visualization Tools
Platforms like Gephi and Graphviz let you visualize state transitions, making complex models more intuitive.





