Moving averages are your secret weapon for smoothing out short-term fluctuations and highlighting longer-term trends or cycles. By analyzing these averages, you can detect anomalies that might otherwise go unnoticed. In this article, we’ll explore the power of moving averages and their applications in various fields.
Types of Moving Averages
Simple Moving Average (SMA)
The Simple Moving Average (SMA) is a straightforward yet powerful tool. It’s calculated by taking the unweighted mean of the previous n data points. This helps in identifying general trends over time.
Exponential Moving Average (EMA)
The Exponential Moving Average (EMA), on the other hand, places more weight on recent data points, making it more responsive to new information. This makes it particularly useful in dynamic environments.
Applications of Moving Averages
Moving averages are versatile tools with broad applications across various fields. Let’s dive into how they are commonly used to bring clarity and insights in different areas:
Stock Market Analysis
In the stock market, moving averages are essential for identifying trends in stock prices. Traders and analysts rely on these averages to smooth out price fluctuations, revealing the underlying trend. By analyzing Simple Moving Averages (SMA) and Exponential Moving Averages (EMA), investors can detect potential buy and sell signals, aiding in more informed decision-making.
For instance, a crossover strategy where the short-term moving average crosses above a long-term moving average might signal a buying opportunity. Conversely, when the short-term moving average crosses below the long-term moving average, it might indicate a sell signal.
Environmental Monitoring
In environmental monitoring, moving averages help in analyzing pollution levels over time. Environmental scientists use these averages to smooth out daily or weekly variations in data, making it easier to see long-term trends in pollution levels. This is crucial for understanding the impact of regulatory measures, identifying periods of significant change, and making data-driven decisions about environmental policies.
For example, by applying a 30-day moving average to daily air quality index readings, researchers can identify trends that may be associated with seasonal changes, industrial activities, or the implementation of new environmental regulations.
Sales Forecasting
For businesses, moving averages are invaluable in sales forecasting. They help in understanding sales trends and seasonality, allowing companies to anticipate demand and adjust their strategies accordingly. By analyzing past sales data with moving averages, businesses can identify unusual spikes or drops in sales, helping them to prepare for future fluctuations.
Consider a retail company using a 12-month moving average to analyze yearly sales data. This can reveal seasonal patterns, such as increased sales during holidays, enabling the company to stock inventory appropriately and optimize marketing efforts for peak seasons.
Example: Detecting Anomalies in Weekly Sales Data
Using moving averages to detect anomalies in weekly sales data is a practical and effective approach. Here’s a step-by-step guide to using the Simple Moving Average (SMA) for this purpose:
Step 1: Calculate the SMA
First, choose a window size for the moving average. A common choice is 4 weeks. To calculate the SMA:
- Sum the sales data for the chosen window size.
- Divide the sum by the number of weeks in the window.
For instance, if your sales data for four weeks are [200,220,230,250][200, 220, 230, 250][200,220,230,250], the SMA is calculated as follows:
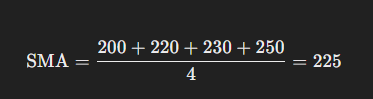
Step 2: Compare Each Week’s Sales Against the SMA
Next, compare the actual sales data for each week against the calculated SMA. Significant deviations from the SMA indicate potential anomalies.
Consider the following weekly sales data for eight weeks:
[200,220,230,250,260,270,280,300][200, 220, 230, 250, 260, 270, 280, 300][200,220,230,250,260,270,280,300]
Calculate the 4-week SMA for week 5:
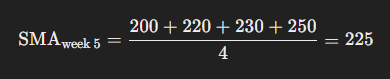
Now, compare the actual sales for week 5 (260) to the SMA (225). Since 260 is significantly higher than 225, it may be flagged as a potential anomaly.
Repeat this process for subsequent weeks:
- Week 6:
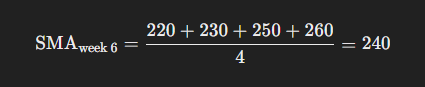
- Actual sales: 270
- Deviation: 270 – 240 = 30 (potential anomaly)
- Week 7:
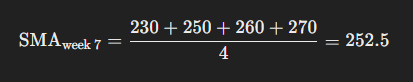
- Actual sales: 280
- Deviation: 280 – 252.5 = 27.5 (potential anomaly)
- Week 8:
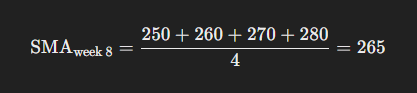
- Actual sales: 300
- Deviation: 300 – 265 = 35 (potential anomaly)
The following figure visualizes the original time series data, the calculated moving average, the confidence intervals, and the detected anomalies.
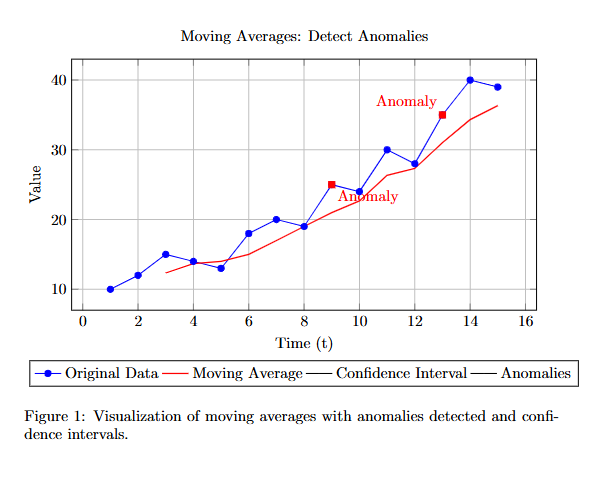
Discussion
Significance of Anomalies
Anomalies can provide valuable insights into the behavior of the system being monitored. They can indicate rare events, system faults, or significant changes in the process. Identifying these anomalies allows for timely intervention and corrective actions.
Challenges in Anomaly Detection
Detecting anomalies in time series data presents several challenges:
- Noise: High levels of noise in the data can obscure anomalies.
- Dynamic Patterns: Time series data may exhibit dynamic patterns that change over time, making it difficult to distinguish anomalies from normal variations.
Identifying Anomalies
Sales values significantly different from the SMA are potential anomalies. In our example, the actual sales for weeks 5, 6, 7, and 8 deviate considerably from their respective SMAs, indicating possible anomalies. These deviations could result from various factors such as promotions, market shifts, or other external influences.
Pros and Cons of Using Moving Averages
Moving averages are powerful tools, but like any analytical method, they come with their advantages and disadvantages. Understanding these can help you make the most of their application in your data analysis.
Pros
Reduces Noise and Clarifies Trends
One of the primary benefits of moving averages is their ability to reduce noise in data. By smoothing out short-term fluctuations, moving averages highlight longer-term trends, making it easier to see the underlying pattern. This is particularly useful in volatile data sets, such as stock prices or daily sales figures.
Easy to Implement and Understand
Moving averages are easy to calculate and straightforward to interpret. Whether you are using a simple moving average (SMA) or an exponential moving average (EMA), the mathematical principles are simple, and the results are easy to visualize and understand. This makes them accessible even for those who may not have a deep background in statistics.
Cons
Lagging Indicator
A significant drawback of moving averages is that they are a lagging indicator. This means they are based on past data, which can delay the detection of new trends or changes in the data. For real-time anomaly detection, this can be a limitation, as moving averages may not react quickly enough to sudden changes.
Subjective Choice of Window Size
The effectiveness of a moving average heavily depends on the choice of window size. This selection can be somewhat subjective and can significantly impact the results. A too-small window may not smooth out enough noise, while a too-large window may oversmooth the data and obscure important trends. Finding the right balance is crucial and can vary depending on the specific data set and analysis goals.
Conclusion
Moving averages are valuable tools for smoothing data and identifying trends, but they are not without their limitations. While they are easy to implement and can reduce noise effectively, they are also lagging indicators and require careful consideration when selecting the window size. By understanding these pros and cons, you can better utilize moving averages in your analysis to make more informed decisions.
FAQ
How Can Moving Averages Detect Anomalies?
To detect anomalies, compare each week’s sales against the calculated SMA. Significant deviations from the SMA indicate potential anomalies. For example, if the SMA is 225 and the actual sales are 260, the difference might suggest an anomaly.
What are the Advantages of Using Moving Averages?
- Reduces Noise: Smoothing out fluctuations clarifies long-term trends.
- Easy to Implement: Calculating and interpreting moving averages is straightforward.
What are the Disadvantages of Using Moving Averages?
- Lagging Indicator: They rely on past data and may not react quickly to sudden changes.
- Subjective Window Size: The choice of window size can significantly impact results and requires careful consideration.
How Do I Choose the Right Window Size?
Choosing the right window size depends on the specific data set and analysis goals. A smaller window may not smooth out enough noise, while a larger window may oversmooth the data, obscuring important trends. It’s often useful to experiment with different window sizes to find the best fit.
Can Moving Averages Be Used in Real-Time Anomaly Detection?
While moving averages are useful for identifying trends, they are less effective for real-time anomaly detection due to their nature as lagging indicators. For real-time applications, more advanced methods like exponential moving averages (EMA) or other statistical techniques may be better suited.
What Are Some Common Applications of Moving Averages?
- Stock Market Analysis: Identifying trends in stock prices.
- Environmental Monitoring: Analyzing pollution levels over time.
- Sales Forecasting: Understanding sales trends and seasonality.
Where Can I Learn More About Moving Averages?
To dive deeper into moving averages and their applications, consider exploring resources such as:
- Investopedia: Moving Average
- Khan Academy: Introduction to Moving Averages
- Coursera: Time Series Analysis
- Environmental Data Analysis with Moving Averages
By understanding the pros, cons, and applications of moving averages, you can effectively use them to analyze data and detect anomalies in various fields.