
AlphaGeometry: Pioneering the Future of Geometric Intelligence
Geometry, the mathematical discipline that explores shapes, sizes, relative positions, and properties of space, has a storied history dating back to ancient civilizations. Traditionally, geometry required painstaking manual calculations and deep theoretical understanding. However, AlphaGeometry is poised to change that narrative by bringing the power of artificial intelligence into the geometric domain. This technology doesn’t just complement our understanding of geometry—it redefines it.
Unpacking AlphaGeometry: The Engine Behind the Revolution
At its core, AlphaGeometry is an advanced AI system designed specifically for geometric computations and spatial analysis. It integrates machine learning algorithms with traditional geometric principles, enabling it to learn from geometric data and improve its performance over time. Unlike generic AI models, AlphaGeometry is finely tuned to handle the intricacies of both 2D and 3D spaces, offering solutions to complex problems that were previously deemed unsolvable or too time-consuming.
AlphaGeometry’s engine uses a combination of deep neural networks and symbolic reasoning. This dual approach allows it to not only compute geometric solutions but also to understand the underlying principles in a way that mimics human intuition. This capability is critical in fields where precision and accuracy are non-negotiable.
Transforming Mathematical Research
Mathematical research, especially in geometry, has traditionally been an arduous process. Researchers often rely on theoretical frameworks and manual proofs to validate hypotheses. AlphaGeometry transforms this process by automating much of the computational heavy lifting. It can quickly generate proofs for geometric theorems, explore new conjectures, and provide visual representations that aid in the comprehension and communication of complex ideas.
Moreover, AlphaGeometry’s ability to simulate non-Euclidean geometries—such as hyperbolic and spherical geometries—opens new avenues in mathematical research. These non-standard geometries are crucial in areas like cosmology, quantum physics, and even artificial intelligence, where traditional Euclidean geometry falls short.
Enhancing Engineering and Robotics
In the fields of engineering and robotics, precision and efficiency are key. Engineers often face the challenge of optimizing designs within tight constraints, whether it’s minimizing material usage or ensuring that a structure can withstand environmental stresses. AlphaGeometry aids in this process by rapidly generating geometric optimizations that meet specified criteria.
In robotics, understanding and navigating space is fundamental. Robots rely on accurate geometric computations to move and interact with their environment. AlphaGeometry enhances robotic systems by providing real-time spatial analysis and pathfinding capabilities. This allows robots to navigate complex environments with greater accuracy, improving their performance in tasks ranging from industrial automation to space exploration.

Revolutionizing 3D Modeling and Simulation
3D modeling is a field that spans multiple industries, from entertainment to manufacturing. The traditional process of creating accurate 3D models is labor-intensive and requires a high level of expertise. AlphaGeometry simplifies this by automating much of the modeling process. It can quickly generate complex 3D structures from basic parameters, ensuring both accuracy and consistency.
In simulation, AlphaGeometry’s capabilities are equally impressive. Simulating physical environments often requires accurate geometric representations to ensure realism. AlphaGeometry can create these representations and simulate their behavior under various conditions, providing valuable insights for industries such as automotive design, aviation, and urban planning.
Application in Modern Physics
Modern physics increasingly relies on advanced mathematical frameworks to describe the universe. General relativity and string theory, for example, are deeply rooted in complex geometric concepts. AlphaGeometry is uniquely positioned to assist physicists in exploring these theories by providing tools that can model and simulate geometric structures in high-dimensional spaces.
AlphaGeometry’s ability to handle multi-dimensional spaces is particularly relevant in the study of black holes, cosmic inflation, and quantum gravity. These areas require precise calculations that go beyond the capabilities of traditional methods, and AlphaGeometry’s AI-driven approach offers a new level of accuracy and insight.
Accelerating Architectural Innovation
Architecture is an art form that relies heavily on geometry. From the Gothic cathedrals of the Middle Ages to the modern skyscrapers of today, geometric principles have guided architectural design. However, the complexity of modern structures often requires advanced tools to ensure that designs are not only aesthetically pleasing but also structurally sound.
AlphaGeometry empowers architects by offering tools that can quickly generate and evaluate complex geometric forms. Whether it’s designing a futuristic cityscape or ensuring the structural integrity of a new building, AlphaGeometry’s AI-driven analysis can optimize designs in ways that were previously impossible. This not only speeds up the design process but also allows for greater creativity and innovation.
Education: From Abstract to Intuitive
Teaching geometry has always been a challenge, particularly when it comes to conveying abstract concepts to students. AlphaGeometry transforms the educational landscape by providing interactive tools that make learning geometry both intuitive and engaging. These tools allow students to explore geometric concepts through hands-on experiences, making the abstract tangible.
For example, students can use AlphaGeometry to manipulate 3D models in real time, seeing how changes in one dimension affect the whole structure. This dynamic learning environment fosters a deeper understanding of geometric principles and encourages students to explore geometry in ways that static textbooks cannot offer.
Creativity Unleashed in Art and Design
In the realms of art and design, geometry plays a crucial role in creating visual harmony and balance. AlphaGeometry offers artists and designers a new set of tools to explore and manipulate geometric forms. This allows for the creation of intricate patterns, symmetries, and fractals that would be nearly impossible to produce manually.
Digital artists can use AlphaGeometry to generate abstract compositions that push the boundaries of traditional art forms. Similarly, in graphic design, AlphaGeometry’s ability to create perfectly balanced layouts can lead to more visually appealing and effective designs.
The Ethical Implications and Future Directions
As with any powerful technology, AlphaGeometry brings with it ethical considerations. The automation of complex geometric processes raises questions about the future of jobs in fields like architecture, engineering, and design. While AlphaGeometry can vastly improve efficiency and open new creative avenues, it also challenges traditional roles and skillsets.
The future of AlphaGeometry may lie in its integration with other emerging technologies. For instance, combining AlphaGeometry with augmented reality (AR) could revolutionize how we interact with and understand space. Imagine architects walking through a virtual model of a building before it’s even constructed, or students using AR to explore geometric shapes in a fully immersive environment.
The Power of Synthetic Data
One of AlphaGeometry’s standout features is its ability to generate and use vast amounts of synthetic data. The system was trained using a billion random geometric diagrams, which were filtered down to 100 million unique examples. This extensive training allows AlphaGeometry to predict and add constructs to solve complex problems (Learn R, Python & Data Science Online).
Real-World Applications
Solving Olympiad Problems
AlphaGeometry has been tested on problems from the International Mathematical Olympiad (IMO). It successfully solved 25 out of 30 problems, a performance comparable to top human contestants. This achievement showcases AI’s potential in advanced mathematical problem-solving .
Beyond Mathematics
The implications of AlphaGeometry extend beyond geometry. Its problem-solving capabilities can be applied in fields like computer vision, architecture, and theoretical physics. For instance, in architecture, AI can optimize spatial designs, and in computer vision, it can enhance object recognition .
How Does AlphaGeometry Work?
- Symbolic Deduction: The symbolic engine analyzes geometric diagrams and derives new statements about their properties.
- Neural Predictions: If the engine stalls, the neural model suggests new constructs to explore.
- Iteration: This loop continues until a solution is found, with the neural model guiding the symbolic engine (Google DeepMind).
Training and Data Generation
DeepMind’s approach to training involved generating large-scale synthetic data. The AI created diagrams and derived proofs, learning from millions of examples. This method bypasses the need for extensive human input, making the system highly scalable ).
Ethical Considerations
While AlphaGeometry is a significant leap forward, it raises ethical questions. The use of synthetic data and the AI’s ability to surpass human capabilities in specific tasks necessitates discussions on the broader implications of such technologies in education and professional fields.
Detailed Technical Insights
Neuro-Symbolic Systems
The integration of neuro-symbolic systems in AlphaGeometry is revolutionary. Neural language models are adept at identifying patterns and suggesting constructs, but they lack the rigor for formal proofs. The symbolic deduction engine compensates for this by applying formal logic to validate these constructs, ensuring robust and accurate solutions.
Synthetic Data Generation
The generation of synthetic data at scale is a major innovation. By creating billions of diagrams and deriving relationships among geometric objects, AlphaGeometry trains on a diversity of problems far beyond what human-generated datasets could offer. This method ensures the AI can handle a wide range of geometric challenges.
AlphaGeometry in Action
Geometry in Education
AlphaGeometry revolutionizes education by providing advanced tutoring systems. These systems help students grasp difficult concepts through step-by-step solutions and explanations. Imagine students in a classroom, using AlphaGeometry on their laptops to solve complex problems, with the AI projected on a screen, guiding them through each step.
Architectural Design
In architecture, AlphaGeometry optimizes building designs by efficiently solving spatial problems. This leads to innovative and functional architectural solutions, enhancing both aesthetics and usability. Picture an architect’s initial sketch transformed into a refined design with AlphaGeometry’s suggestions, showing improved structural elements and aesthetics.
Computer Vision
AlphaGeometry improves computer vision systems, especially in tasks involving spatial reasoning and object recognition. This enhancement benefits applications in robotics, autonomous vehicles, and surveillance systems. Imagine a drone navigating a dense forest with enhanced algorithms from AlphaGeometry, successfully avoiding obstacles.
Real-World Examples
Example 1: Solving Geometry Problems
Problem: Given a triangle ABC with sides aaa, bbb, and ccc, and an angle α\alphaα opposite side aaa, find the area of the triangle.
Solution: AlphaGeometry uses the formula for the area of a triangle when two sides and the included angle are known:
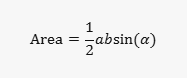
By inputting the values of sides aaa and bbb, and the measure of angle α\alpha α, AlphaGeometry calculates the area of triangle ABC. This example shows how AlphaGeometry applies mathematical formulas to solve geometry problems
Example 2: Right-Angled Triangle
Problem: In a right-angled triangle ABC, where angle C is the right angle, if side AB (the hypotenuse) is 10 units long and side AC is 6 units long, find the length of side BC.
Solution: AlphaGeometry uses the Pythagorean theorem:
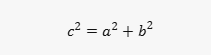
Given that AB = 10 units and AC = 6 units, we can find BC as follows:
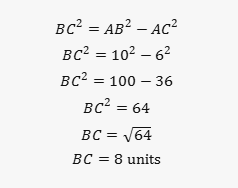
So, the length of side BC is 8 units. AlphaGeometry performs such calculations quickly and accurately for a wide range of geometric problems (MIT Technology Review).
Non-Euclidean Geometries
AlphaGeometry handles various geometric problems, including non-Euclidean geometries like hyperbolic and elliptic geometry. In hyperbolic geometry, the sum of the angles in a triangle is less than 180 degrees, while in elliptic geometry, it is greater than 180 degrees. AlphaGeometry uses specific models, such as the Poincaré disk model or the hyperboloid model, to solve problems within these frameworks.
Future Prospects
Expanding to Other Mathematical Domains
AlphaGeometry’s success in geometry opens the door to applications in other mathematical domains like algebra and calculus. Researchers aim to adapt the neuro-symbolic approach, potentially leading to breakthroughs in mathematical research and education.
Advanced Problem-Solving
AlphaGeometry positions itself as a critical tool in scientific research by solving increasingly complex problems. By applying AI to explore unsolved mathematical problems, it uncovers new theories and insights, advancing our understanding of the universe.
AI in Research Mathematics
Future developments aim to tackle advanced, abstract problems in research mathematics. This leap could significantly impact fields that rely on deep mathematical insights, such as theoretical physics and advanced engineering.
How can I access or use AlphaGeometry for my own geometry problems?
To access or use AlphaGeometry for your own geometry problems, you would typically need to follow these steps:
- Research: Look for academic papers or official publications that detail AlphaGeometry’s capabilities and how it can be accessed.
- Academic Institutions: Check if any universities or research institutions have access to AlphaGeometry and if they offer any resources or tools for external users.
- Collaboration: Reach out to the developers or researchers behind AlphaGeometry to inquire about potential collaboration opportunities or access to the system.
- Open Source Alternatives: Explore open-source AI systems that are designed for geometry problem-solving, which may offer similar functionalities.
It’s important to note that AlphaGeometry is a specialized tool developed by Google DeepMind, and access to it may be restricted to certain research environments. If you’re interested in using AI for geometry problems, you might consider looking into other AI platforms that are more accessible and provide tools for mathematical problem-solving.
Conclusion
AlphaGeometry represents a major advancement in AI, blending intuitive predictions with rigorous logic to solve complex problems. Other AI systems may also handle non-Euclidean geometries, but AlphaGeometry’s integration of deep learning with symbolic logic gives it an edge in understanding and solving these types of problems.
Its success in competitions like the International Mathematical Olympiad Geometry Shiven highlights its capabilities in this area. Its applications span various fields, enhancing our understanding and capabilities in geometry and beyond. As AI continues to evolve, AlphaGeometry paves the way for innovative solutions and groundbreaking discoveries in mathematical problem-solving.
People Also Ask
What is AlphaGeometry and how does it revolutionize AI in geometry?
AlphaGeometry is an advanced AI model designed to tackle complex geometric problems. It integrates sophisticated algorithms with deep learning techniques to provide accurate and efficient solutions for geometric computations and visualizations, significantly enhancing traditional methods used in fields such as computer graphics, engineering, and mathematics.
How does AlphaGeometry differ from traditional geometry software?
AlphaGeometry utilizes deep learning and AI algorithms to automatically learn and solve geometric problems, whereas traditional geometry software typically relies on predefined rules and manual inputs. This enables AlphaGeometry to handle more complex and abstract geometric challenges with greater efficiency and accuracy.
What are the main applications of AlphaGeometry in real-world scenarios?
AlphaGeometry can be applied in various fields including architecture, engineering, computer graphics, and robotics. It aids in tasks such as structural analysis, 3D modeling, automated design generation, and spatial reasoning, providing innovative solutions that traditional methods may struggle to achieve.
How does AlphaGeometry improve the accuracy of geometric computations?
AlphaGeometry leverages machine learning models trained on vast datasets of geometric problems and solutions. This training allows it to recognize patterns and make predictions with high precision, thus improving the accuracy of geometric computations compared to traditional methods which may be limited by predefined rules and algorithms.
Can AlphaGeometry be integrated with existing CAD software?
Yes, AlphaGeometry is designed to be compatible with popular CAD (Computer-Aided Design) software. It can enhance the capabilities of these systems by providing advanced geometric analysis and automated solution generation, making the design process more efficient and innovative.
What are the educational benefits of using AlphaGeometry?
AlphaGeometry offers significant educational benefits by providing students and educators with advanced tools for exploring and understanding complex geometric concepts. It allows for interactive learning experiences, where users can visualize and manipulate geometric shapes and structures, fostering a deeper understanding of the subject.
How does AlphaGeometry handle complex 3D modeling tasks?
AlphaGeometry excels in handling complex 3D modeling tasks by using AI algorithms to automate the design and optimization processes. It can generate detailed 3D models from basic inputs, perform structural analysis, and suggest improvements, making it a powerful tool for industries requiring precise and intricate 3D modeling.
What are the advantages of using AlphaGeometry in architecture and engineering?
In architecture and engineering, AlphaGeometry provides advantages such as automated structural analysis, optimized design solutions, and enhanced visualization capabilities. These features help professionals create more efficient, safe, and aesthetically pleasing structures while reducing the time and effort required for manual calculations and design iterations.
How does AlphaGeometry contribute to advancements in computer graphics?
AlphaGeometry contributes to advancements in computer graphics by providing powerful tools for geometric modeling, rendering, and animation. Its AI-driven approach enables the creation of highly detailed and realistic visualizations, pushing the boundaries of what is possible in digital art, game development, and virtual reality.
Is AlphaGeometry accessible to small businesses and independent developers?
Yes, AlphaGeometry is designed to be accessible to a wide range of users, including small businesses and independent developers. It offers scalable solutions that can be tailored to specific needs and budgets, allowing even smaller entities to leverage advanced geometric computing capabilities without the need for extensive resources.