Quintic functions, characterized by their fifth-degree polynomial form [math]f(x)=ax
5
+bx
4
+cx
3
+dx
2
+ex+f, [/math] are versatile in modeling phenomena with intricate behaviors. These functions exhibit up to five critical points and four inflection points, making them suitable for describing complex systems across various fields.
Understanding Quintic Functions
What Makes Quintic Functions Unique?
Quintic functions are more complex than cubic or quartic functions, allowing them to represent processes with multiple turning points and varying rates of change.
- Higher Complexity: Quintic functions can model systems with non-linear relationships and rapid oscillations.
- Non-Solvable by Radicals: Unlike quadratic, cubic, and quartic equations, general quintic equations cannot be solved algebraically using radicals, a property known as the Abel–Ruffini theorem.
Key Properties of Quintic Functions
- Up to five real roots and four turning points.
- Their graphs often display multiple maxima and minima, making them ideal for capturing nuanced behaviors in systems.
Applications in Physics
Modeling Wave and Oscillation Phenomena
Quintic functions frequently appear in wave mechanics, particularly in solving non-linear Schrödinger equations for wave propagation.
- Application Example: In fiber optics, quintic terms model non-linear dispersion in waveguide systems.
- Real-world relevance: Predicting signal behavior in high-speed optical communication networks.
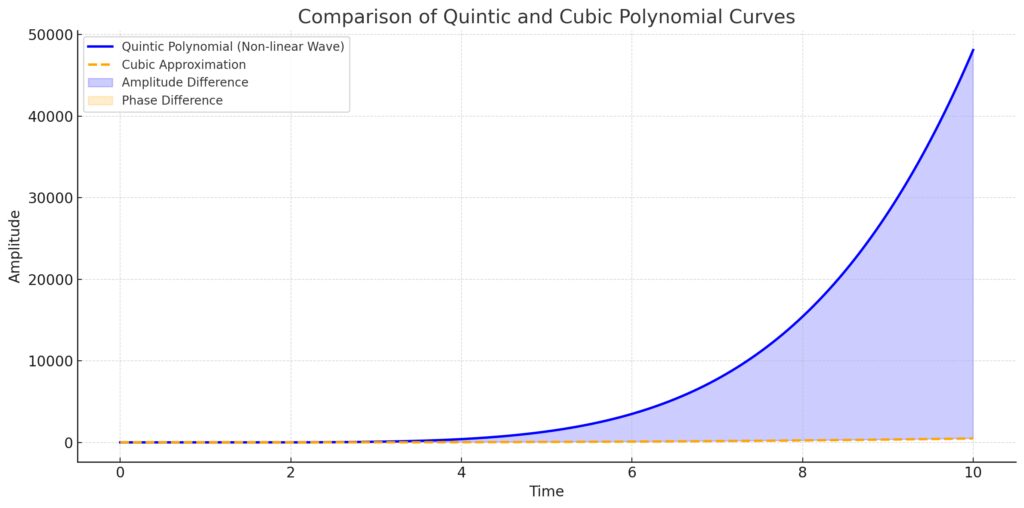
Represents the more complex non-linear wave propagation.
Displayed in blue.
Cubic Approximation:
A simpler model for comparison.
Shown in orange with a dashed line.
Highlighted Differences:
Amplitude Differences: Blue shaded areas where the quintic curve exceeds the cubic approximation.
Phase Differences: Orange shaded areas where the cubic approximation exceeds the quintic curve.
Phase Transitions in Materials
In thermodynamics and material science, quintic functions describe systems with complex energy landscapes, such as phase transitions in crystalline structures.
- Application Example: Modeling the potential energy of atoms in a lattice as they transition between stable and unstable states.
Applications in Engineering
Robotics and Path Planning
In robotics, quintic functions are widely used in trajectory planning for robotic arms and autonomous vehicles.
- Application Example: Designing smooth, continuous motion paths that minimize abrupt changes in velocity or acceleration.
- Key Advantage: Quintic functions’ higher degree allows for finer control over jerk (the rate of change of acceleration).
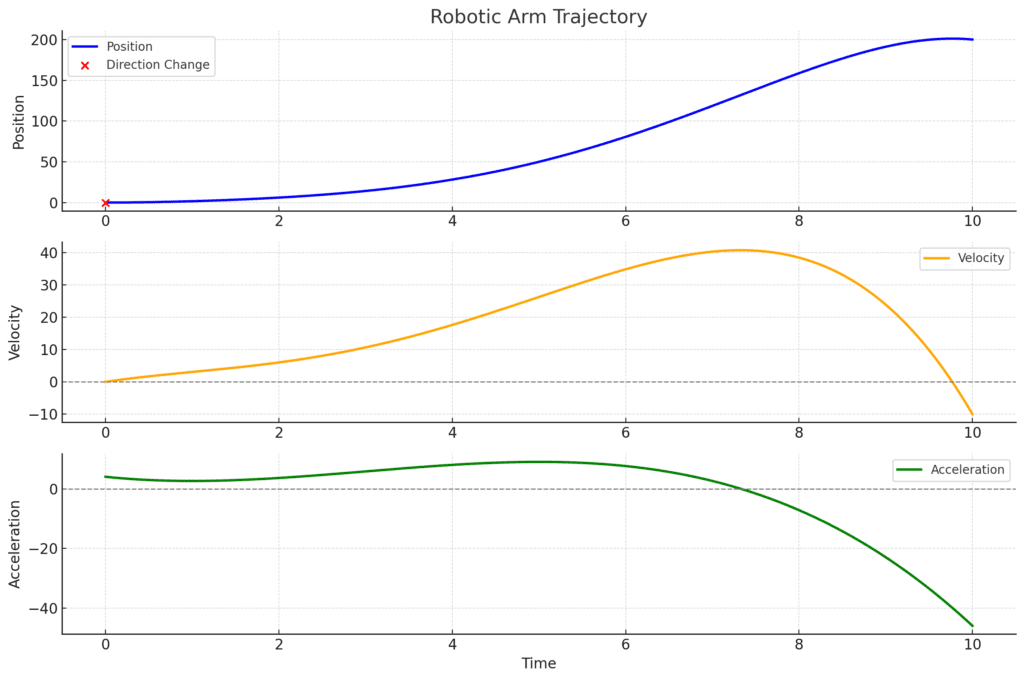
Smooth trajectory over time, represented by a quintic polynomial.
Red points highlight where the arm changes direction, minimizing jerks.
Velocity (Middle Plot):
Velocity transitions smoothly, crossing zero at direction change points.
A horizontal dashed line marks [math]v=0[/math].
Acceleration (Bottom Plot):
Smooth variations in acceleration ensure minimal jerks.
The dashed line indicates[math]a=0[/math], showing transition points for acceleration.
Structural Engineering
Quintic polynomials are utilized in beam deflection analysis under complex load conditions.
- Application Example: Calculating bending moments and deformations in bridges and buildings subjected to non-uniform loads.
Applications in Economics
Forecasting Non-Linear Trends
Quintic functions help economists and data scientists model intricate market behaviors and economic growth trends.
- Application Example: Predicting fluctuations in commodity prices influenced by multiple interacting variables.
- Why Quintic?: The function’s ability to represent multi-peak trends reflects real-world market dynamics.
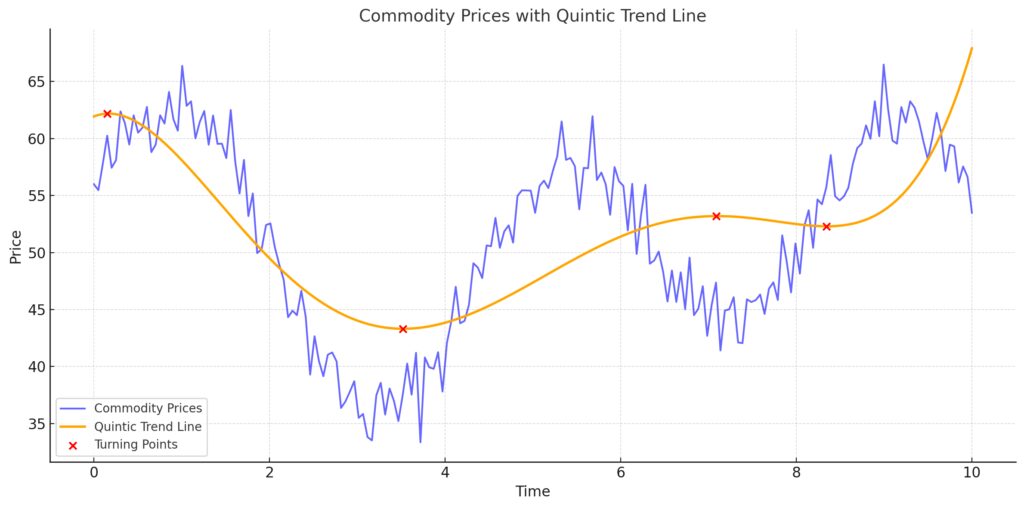
Captures noisy fluctuations in commodity prices over time.
Includes sharp increases and slow declines.
Quintic Trend Line (Orange Line):
Smoothly fits the data, capturing multi-peak behaviors and underlying trends.
Models both sharp increases and slow declines effectively.
Turning Points (Red Markers):
Highlight local maxima and minima in the trend line.
Represent key moments of price reversals.
Game Theory and Optimization
Quintic functions appear in optimization problems with complex constraints and objectives.
- Application Example: Modeling payoff functions in competitive scenarios where outcomes depend on multiple strategic decisions.
Applications in Computer Graphics
Curve Design and Animation
Quintic Bézier curves and splines are extensively used for designing smooth, visually appealing curves in computer graphics and animation.
- Application Example: Creating motion paths for animated characters or camera movements in 3D environments.
- Benefit: Quintic splines offer greater flexibility than cubic curves, enabling intricate designs without sharp transitions.
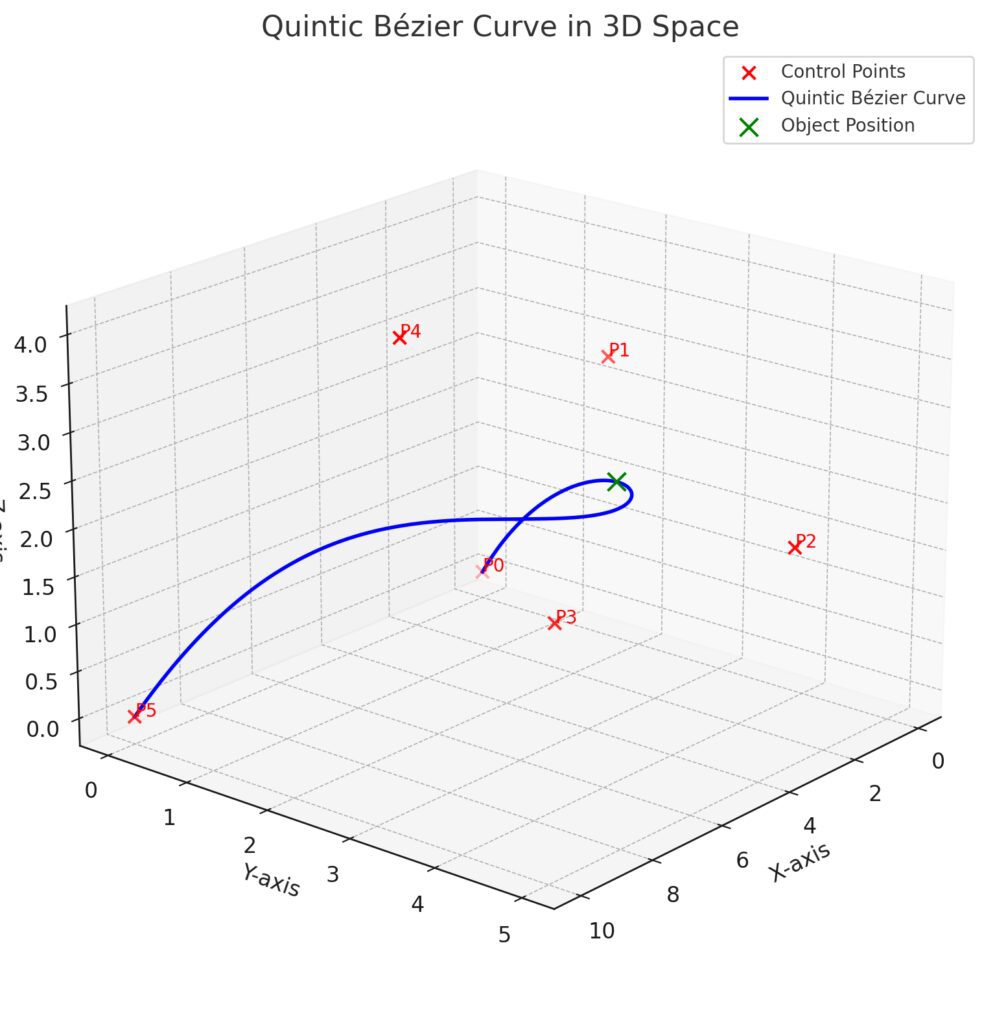
Define the path of the Bézier curve.
Smooth transitions are guided by these points.
Quintic Bézier Curve (Blue Line):
Represents the motion path smoothly adjusting between control points.
Animated Object (Green Marker):
Illustrates a position along the curve (e.g., at 25% of the trajectory).
Procedural Terrain Generation
In video game development, quintic functions are used to model realistic terrain and landscape features.
- Application Example: Simulating undulating hills and valleys with controlled variations in steepness.
Applications in Biology
Population Dynamics
Quintic functions model ecosystems where species interactions lead to fluctuating population sizes over time.
- Application Example: Predicting population cycles in predator-prey systems with additional environmental factors.
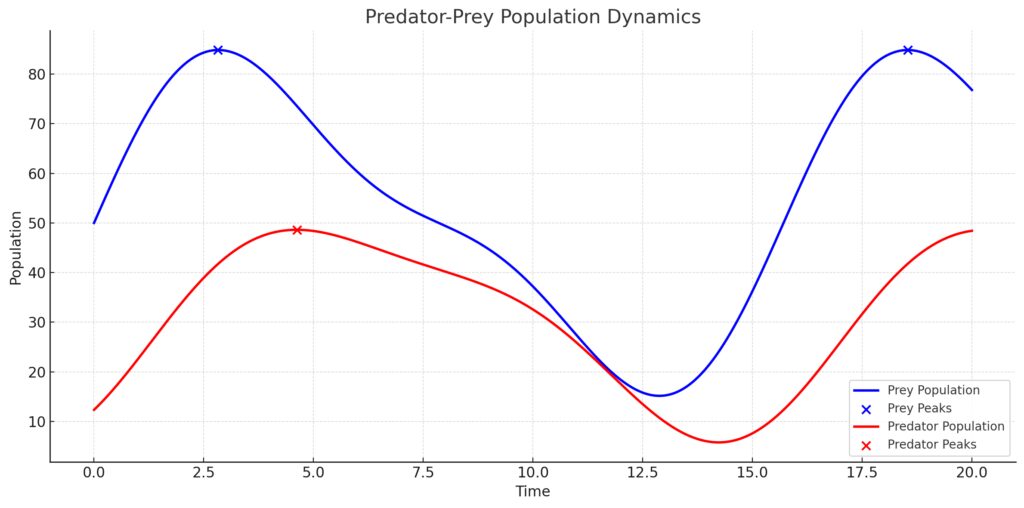
Exhibits oscillatory behavior modeled by a quintic function.
Peaks (Blue Markers): Indicate times of maximum prey population.
Predator Population (Red Line):
Oscillates with a phase lag relative to the prey population, representing predator-prey interactions.
Peaks (Red Markers): Highlight times of maximum predator population.
Cellular Growth and Morphogenesis
In developmental biology, quintic functions describe growth patterns and morphological changes in cells and tissues.
- Application Example: Simulating the curvature and folding of tissues during embryonic development.
Applications in Astronomy and Astrophysics
Orbital Mechanics
Quintic functions arise in equations governing non-linear orbital perturbations in planetary systems.
- Application Example: Calculating deviations in satellite trajectories caused by gravitational influences of multiple celestial bodies.
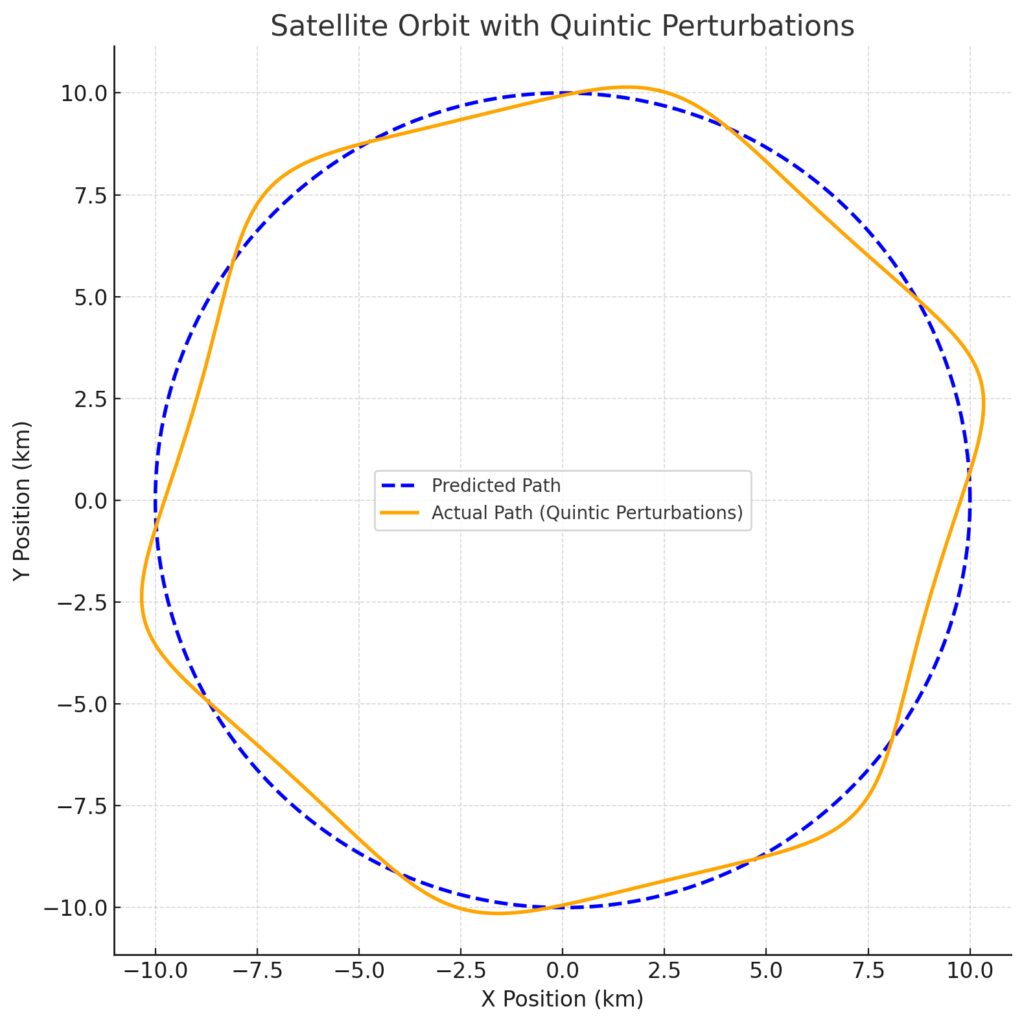
Predicted Path (Blue Dashed Line):
- Represents the ideal circular orbit without external influences.
Actual Path (Orange Line):
Models the satellite’s actual trajectory, incorporating quintic perturbations to account for gravitational variances and other external forces.
Stellar Dynamics
Quintic terms are used to model complex interactions in multi-body systems such as star clusters.
- Application Example: Predicting star motion influenced by both gravitational forces and external disturbances.
Applications in Music and Acoustics
Sound Synthesis and Waveforms
In sound design, quintic functions model waveforms for creating unique tonal qualities and effects.
- Application Example: Generating harmonics and overtones in digital music synthesis software.
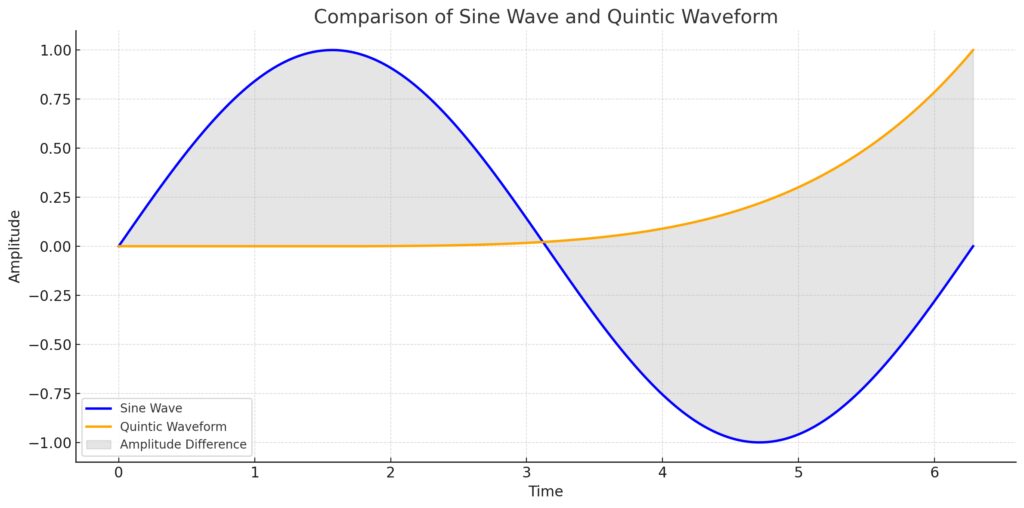
A simple, smooth periodic waveform with constant amplitude and frequency.
Quintic Waveform (Orange Line):
Displays more complex harmonics due to the quintic polynomial model.
Features variations in amplitude and frequency compared to the sine wave.
Amplitude Differences:
Highlighted by the shaded gray regions, showing where the quintic waveform diverges from the sine wave.
Acoustic Engineering
Quintic equations are used to design structures with specific resonant properties, such as concert halls or soundproofing panels.
- Application Example: Optimizing wall curvature to enhance sound quality and reduce echo.
Quintic functions’ ability to model complexity, non-linearity, and oscillatory behavior makes them indispensable across diverse scientific and engineering fields.
FAQs
Why can’t quintic equations be solved using radicals?
The Abel-Ruffini theorem states that general quintic equations cannot be solved algebraically using radicals, unlike quadratic, cubic, or quartic equations. This is because quintic equations can exhibit behaviors that transcend the solutions available through simpler algebraic methods.
Example: While solving a cubic equation for the trajectory of a projectile is straightforward, a quintic equation representing orbital perturbations requires numerical methods or approximations.
How are quintic functions used in physics?
In physics, quintic functions often appear in non-linear dynamics and wave propagation problems, such as modeling dispersion effects in optical fibers or describing energy landscapes in phase transitions.
Example: A fiber optic system may use a quintic term to represent non-linear dispersion, helping engineers design more efficient high-speed communication systems.
What makes quintic functions ideal for trajectory planning in robotics?
Quintic functions provide a higher level of control over motion, allowing precise adjustment of position, velocity, and acceleration while minimizing jerk. This makes them perfect for robotics applications requiring smooth and predictable paths.
Example: A robotic arm moving between two points uses a quintic polynomial to ensure the motion is smooth, avoiding abrupt stops or accelerations that could damage components.
Can quintic functions handle real-world market trends?
Yes, quintic functions are suitable for modeling non-linear trends in economic and market data, especially when there are multiple peaks and troughs over time.
Example: In commodity price forecasting, quintic trend lines can capture the complexity of price fluctuations influenced by factors like supply shortages or geopolitical events.
How do quintic Bézier curves enhance computer graphics?
Quintic Bézier curves allow for smooth, flexible design in animations and graphic modeling, accommodating intricate shapes and movements that require fine-tuned control.
Example: In video game design, a quintic Bézier curve might define the flight path of an animated object, ensuring it appears natural and visually appealing.
Are quintic functions used in biology?
Yes, quintic functions model biological processes with complex dynamics, such as population growth in ecosystems or the folding of tissues during embryonic development.
Example: A quintic function might predict predator-prey cycles in a forest ecosystem, where multiple environmental and interspecies factors lead to fluctuating populations over time.
How are quintic equations solved in practice if not by radicals?
Numerical methods like Newton-Raphson or iterative algorithms are commonly used to approximate the roots of quintic equations. These approaches are computationally intensive but effective.
Example: Engineers designing a suspension bridge may use software to solve a quintic equation representing the deflection curve under a variable load.
Can quintic functions model sound or music?
Quintic functions are often used in sound synthesis to create waveforms with complex harmonic structures, enhancing tonal richness in music production.
Example: A quintic waveform might be used in synthesizers to produce unique sounds with layered overtones for modern electronic music compositions.
Why are quintic functions relevant in astronomy?
Quintic functions appear in astrophysical models to describe complex orbital mechanics, such as perturbations in satellite trajectories caused by gravitational influences from multiple celestial bodies.
Example: Predicting the orbit of a space probe near a planet requires quintic equations to account for the intricate gravitational interactions over time.
How are quintic functions used in structural engineering?
Quintic functions are vital for modeling deformations in structures under variable loads. They accurately describe deflection curves in beams and bridges, considering bending moments and complex forces.
Example: A quintic polynomial helps predict how a bridge deforms under uneven vehicle weights, ensuring structural integrity and safety.
Can quintic functions represent natural phenomena?
Yes, quintic functions are frequently used to model natural processes that exhibit non-linear and oscillatory behavior, such as water wave dynamics or terrain variations.
Example: In hydrodynamics, quintic polynomials help simulate the crest and trough shapes of complex waves, aiding in flood prediction models.
Why are quintic functions useful in optimization problems?
Quintic functions allow the representation of cost functions or energy states with multiple local minima and maxima, making them ideal for solving multi-objective optimization problems.
Example: In supply chain logistics, quintic functions model transportation costs considering multiple constraints, such as fluctuating fuel prices and delivery times.
How do quintic functions compare to cubic or quartic functions?
Quintic functions provide more flexibility than cubic or quartic functions due to their higher degree, which allows for more critical points and inflection points. This makes them better suited for problems requiring finer detail and complexity.
Example: In animation, a quintic curve may be used to design more intricate motion paths than a cubic spline, accommodating additional turning or transition points.
Can quintic functions model population dynamics in ecosystems?
Yes, quintic functions can represent the complex, non-linear interactions in ecosystems, such as predator-prey relationships or resource competition.
Example: A quintic model predicts how a predator species’ population peaks after prey abundance, followed by a decline due to overconsumption and resource scarcity.
Are quintic functions computationally expensive to use?
While quintic functions are more complex than lower-degree polynomials, modern computational tools efficiently handle their evaluation and root-finding. However, real-time applications may require approximations for speed.
Example: In video game terrain generation, approximations of quintic functions are used to balance realistic landscapes and fast rendering times.
How do quintic functions appear in finance?
Quintic functions model intricate behaviors in financial markets, capturing trends with multiple inflection points caused by factors like economic policies, investor sentiment, or global events.
Example: A quintic model might depict stock market trends over a volatile period, showing rapid rises, corrections, and recoveries.
Are quintic functions used in machine learning?
Although not commonly a default choice, quintic functions can act as feature transformations or basis functions in regression models for capturing non-linear relationships in data.
Example: In predictive analytics for customer behavior, quintic polynomials help uncover subtle patterns in purchase histories influenced by marketing campaigns.
How are quintic functions visualized?
Quintic functions are typically visualized as curves on a 2D plane, showing their critical points, turning points, and inflection points. 3D visualizations may also be used when quintic functions are extended to multiple variables.
Example: A graph of a quintic function modeling wave behavior might display oscillatory peaks and troughs with labels for each critical point.
Do quintic functions have applications in control systems?
Yes, quintic functions are used to design control systems with smooth transitions between states, minimizing disruptions in dynamic systems.
Example: In automotive cruise control systems, a quintic polynomial ensures smooth acceleration and deceleration curves for a comfortable ride.
Resources
Books and Academic Texts
- “Introduction to the Theory of Algebraic Equations” by Leonard Eugene Dickson
- A foundational text covering quintic functions and the unsolvability of general quintic equations.
- Find it here.
- “Mathematical Methods for Physics and Engineering” by Riley, Hobson, and Bence
- Explores the use of quintic and other higher-order functions in physics and engineering applications.
- “Numerical Recipes: The Art of Scientific Computing” by Press et al.
- Covers numerical solutions for polynomial equations, including quintic functions.
- Visit Numerical Recipes.
- “Advanced Engineering Mathematics” by Erwin Kreyszig
- Details the role of quintic functions in engineering, including deflection curves and trajectory planning.
Online Courses and Tutorials
- Khan Academy – Polynomials
- A beginner-friendly introduction to polynomial functions, laying the groundwork for understanding quintics.
- Visit Khan Academy.
- MIT OpenCourseWare – Calculus and Non-linear Dynamics
- Learn how quintic functions appear in advanced calculus and dynamic systems.
- Explore MIT OCW.
- Udemy – Mathematical Modeling for Engineers
- Hands-on tutorials that often include higher-order polynomial functions for solving real-world problems.
- Find it on Udemy.
Research Papers and Case Studies
- “Quintic Bézier Curves and Their Applications in Computer Graphics”
- Research paper detailing how quintic curves enhance smoothness in design and animation.
- Available through SpringerLink or ResearchGate.
- “Numerical Solutions of Quintic Equations in Orbital Mechanics”
- Discusses quintic applications in astrophysical simulations.
- “Polynomial Trajectory Planning for Robotic Arms”
- Explores quintic functions in smooth trajectory generation for automation systems.
Software and Tools
- MATLAB
- Provides built-in functions for solving and visualizing quintic polynomials.
- Learn MATLAB here.
- Wolfram Mathematica
- Ideal for symbolic and numerical analysis of quintic equations.
- Explore Mathematica.
- Python Libraries: NumPy, SymPy, and SciPy
- Use Python for solving and graphing quintic functions. For example:pythonCode kopieren
from scipy.optimize import fsolve def quintic(x): return x**5 - 2*x**4 + x - 1 root = fsolve(quintic, 1) print(root) - Python Documentation.
- Use Python for solving and graphing quintic functions. For example:pythonCode kopieren
- Desmos Graphing Calculator
- Interactive and user-friendly for visualizing quintic functions.
- Try Desmos.
Interactive and Visual Resources
- Geogebra
- A dynamic tool for visualizing polynomial functions, including quintics, in 2D and 3D.
- Access Geogebra.
- Brilliant.org – Advanced Algebra and Calculus
- Interactive problem sets and explanations on quintic and higher-order polynomials.
- Visit Brilliant.
- Wolfram Alpha
- Quickly solve or visualize quintic equations online with step-by-step explanations.
- Use Wolfram Alpha.