Fine-tuning deep learning models is a critical step in achieving optimal performance for specific tasks. One optimization tool, AdamW, has gained popularity, largely because of its unique handling of weight decay.
But why does weight decay matter, and how does it elevate your training process? Let’s dive in.
What Is Weight Decay in Optimization?
The Role of Regularization in Deep Learning
In machine learning, regularization prevents overfitting by encouraging simpler models. It reduces the risk of your model becoming too tailored to training data and failing to generalize. Weight decay is a common regularization method.
Simply put, weight decay applies a penalty to large parameter values. By constraining the size of the weights, it encourages more stable and interpretable models.
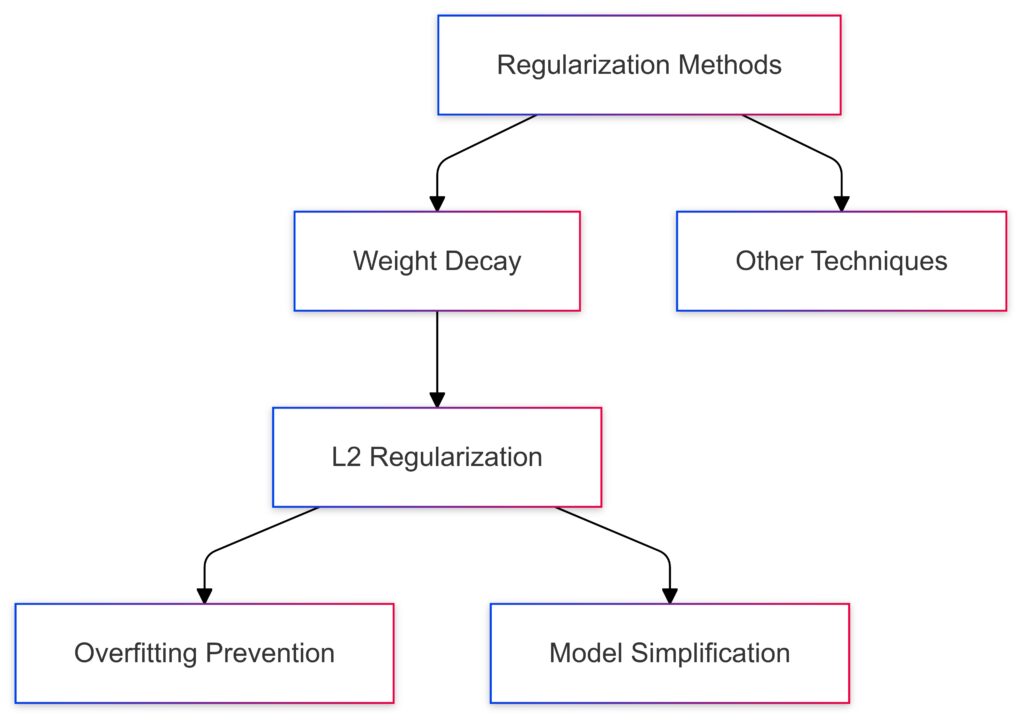
A visual breakdown of weight decay within the broader family of regularization methods.
How Weight Decay Works in Gradient Descent
Weight decay modifies the gradient descent update rule. Instead of only adjusting weights based on gradients, it subtracts a small proportion of each weight’s current value. This shrinkage keeps the parameters from growing unnecessarily large, which might harm performance.
Why Is AdamW Different from Adam?
The Problem with Standard Adam Optimizer
The Adam optimizer combines the best of momentum-based and adaptive learning rate techniques, making it a go-to for many practitioners. However, its implementation of weight decay isn’t straightforward.
Adam applies weight decay by adding it directly to the loss function. This indirect approach can lead to suboptimal updates, as the penalty influences not just the weights but also the learning rate.
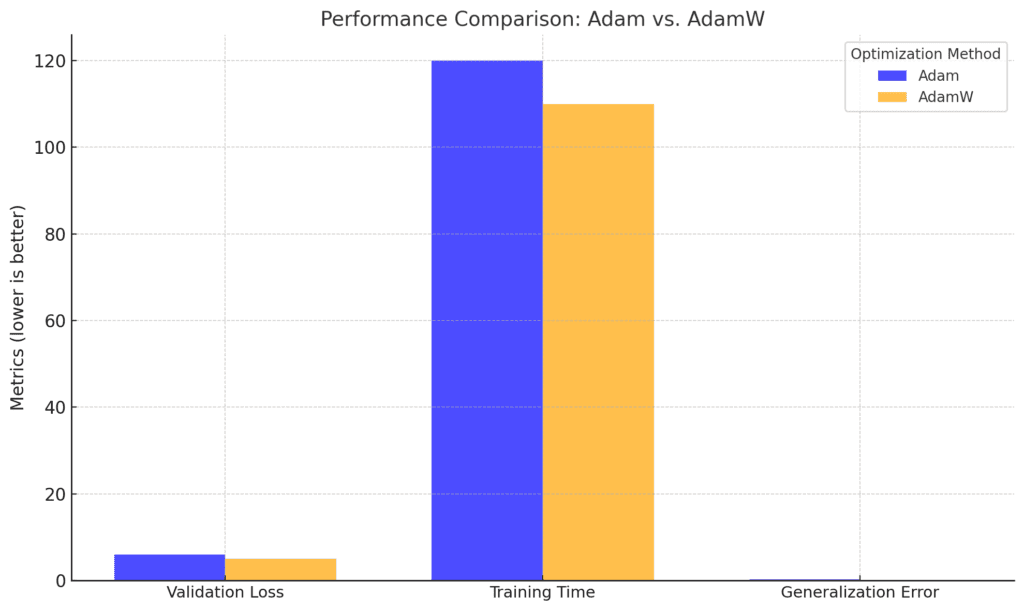
Training Time: AdamW remains faster at 110 units versus 120 for Adam.
Generalization Error: AdamW outperforms Adam with a lower error (0.20 vs. 0.25), emphasizing better generalization.
How AdamW Fixes This Issue
AdamW separates weight decay from the loss function. It applies the penalty directly to weight updates, ensuring that learning rates remain unaffected. This clean decoupling results in more consistent training and often better results, especially for fine-tuning.
By isolating weight decay, AdamW ensures the optimizer performs regularization exactly as intended.
Weight Decay and Model Generalization
Enhancing Stability in Fine-Tuning
Fine-tuning often deals with pre-trained models adapted to specific tasks. Without proper weight decay, models risk overfitting or instability during training. AdamW’s precise implementation helps stabilize training even with small datasets.
Weight Decay and Sparsity
Interestingly, weight decay promotes sparsity in model parameters. Sparse models not only generalize better but are also more interpretable. This property can be particularly beneficial for applications like natural language processing (NLP) and computer vision, where interpretability is key.
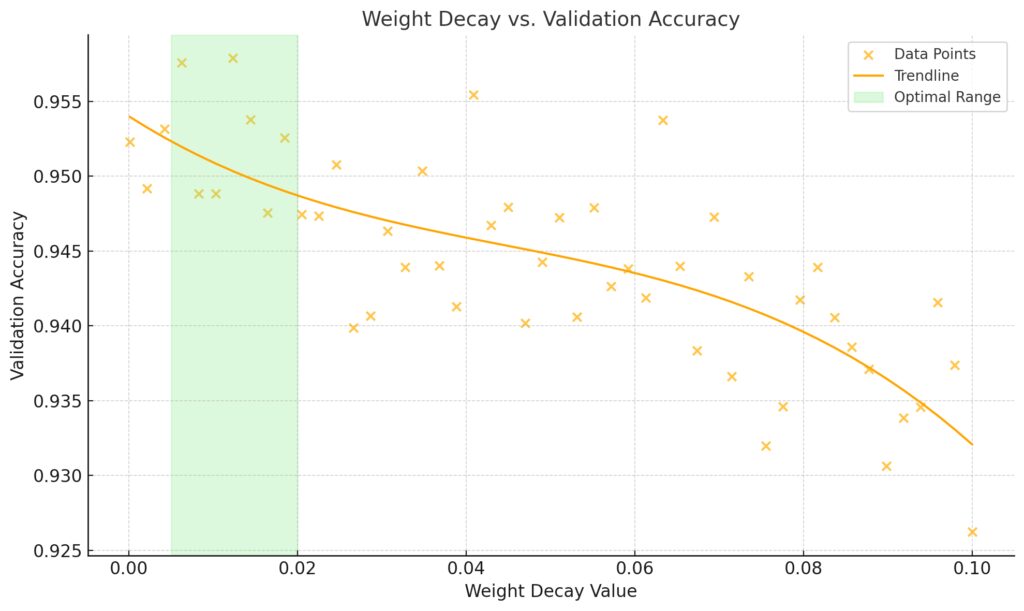
Y-axis: Validation accuracy, indicating model generalization performance.
Trendline: Highlights the general trend, showing a peak in validation accuracy around a specific weight decay range.
Optimal Range: Highlighted in light green (0.005 to 0.02), where generalization performance is maximized.
Choosing the Right Weight Decay Value

Balancing Bias and Variance
Selecting the right weight decay parameter involves balancing bias and variance. A high value may oversimplify the model, introducing bias. Conversely, a low value might not sufficiently control complexity, leading to variance.
Practical Tips for Tuning
- Start with commonly recommended values like
0.01or0.001. - Monitor validation loss carefully.
- Use grid search or Bayesian optimization for more precise tuning.
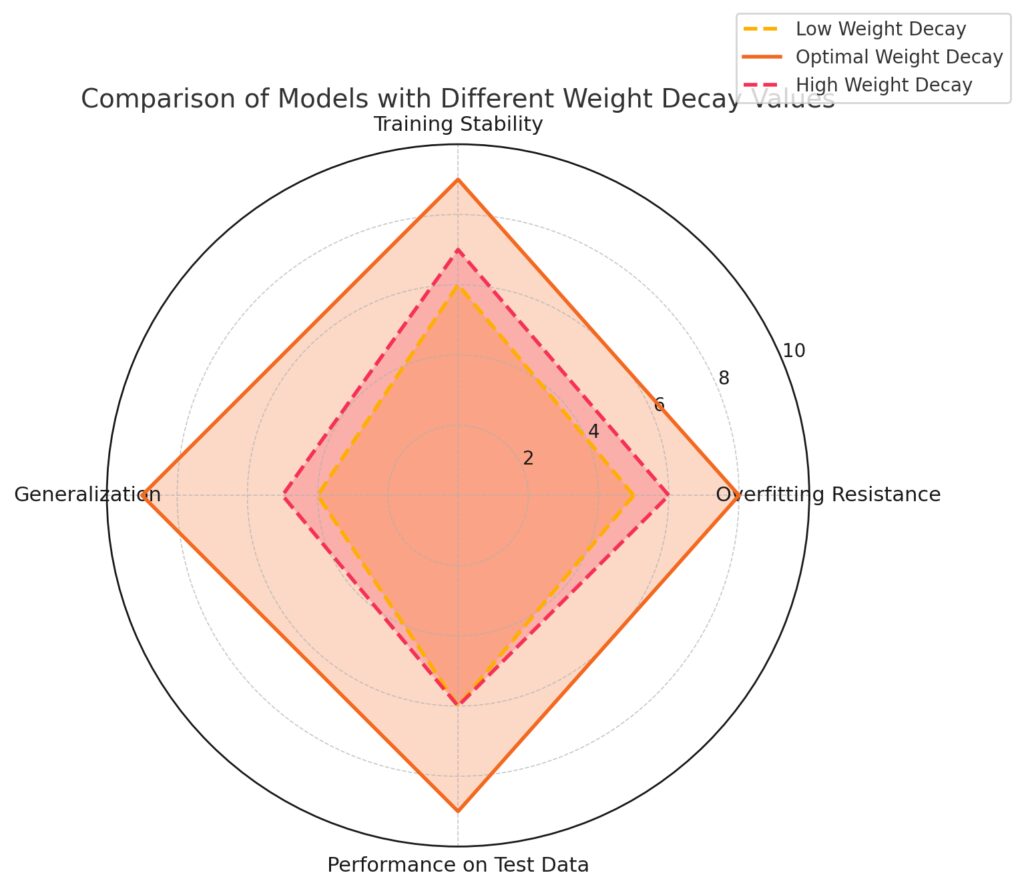
Key Insights:
High Weight Decay: Better than low decay in some aspects but less effective than the optimal setting.
Low Weight Decay: Struggles with overfitting resistance and generalization, showing moderate performance overall.
Optimal Weight Decay: Achieves balanced and superior results across all metrics, demonstrating its effectiveness.
Practical Applications of AdamW with Weight Decay
NLP Fine-Tuning with Transformers
Transformers like BERT and GPT rely heavily on fine-tuning. AdamW ensures these models adapt well to domain-specific tasks without sacrificing generalization.
Computer Vision Models
For image recognition tasks, AdamW shines by stabilizing training in convolutional networks, ensuring better feature extraction.
By handling weight decay effectively, AdamW has become indispensable for researchers and practitioners alike. Fine-tuning success often hinges on this nuanced optimizer.
How AdamW Impacts Model Convergence
Faster Convergence with Precise Regularization
One of AdamW’s standout features is its ability to accelerate convergence without compromising model stability. By separating weight decay from gradient updates, it avoids over-penalizing gradients, which can slow learning in other optimizers.
This makes AdamW particularly effective in fine-tuning pre-trained models, where stability is paramount, and datasets may be smaller.
Smoother Loss Curves
When using AdamW, you’ll often notice smoother loss curves during training. This smoother progression reflects a balanced optimization process, reducing erratic behavior caused by improper weight regularization in older methods.
Challenges with Weight Decay in Fine-Tuning
Over-regularization in Small Datasets
Weight decay is highly effective, but it’s not without risks. When fine-tuning on small datasets, excessive weight decay can lead to underfitting, where the model becomes too simplistic to capture the task’s complexities.
Interaction with Dropout
Dropout is another regularization technique often used in conjunction with weight decay. While the two methods complement each other, improper balance can over-regularize the model, especially in deep architectures like Transformers.
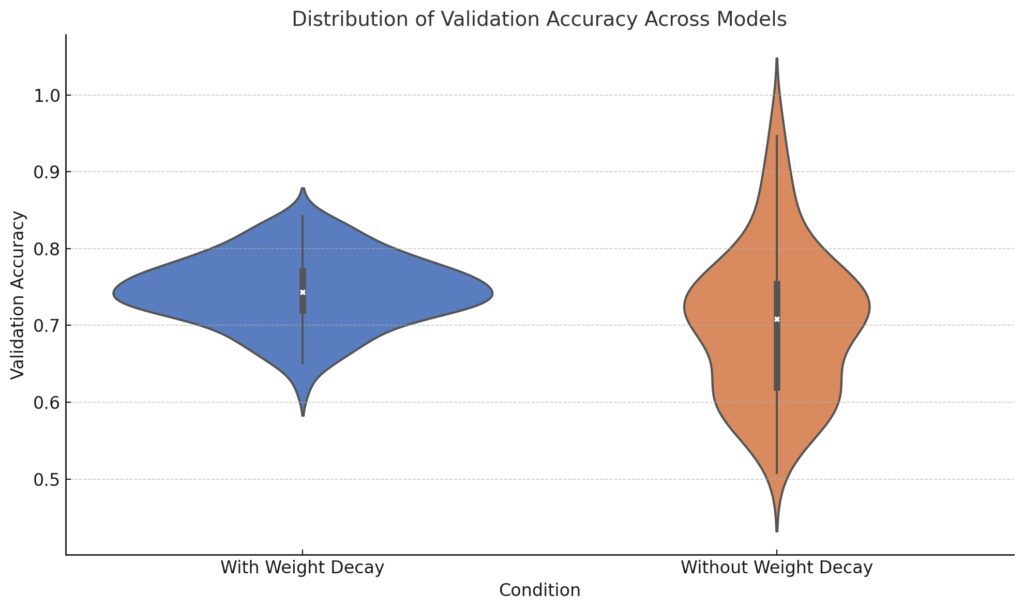
Variance: The models trained without weight decay show a wider spread in accuracy, indicating greater variability in performance.
Median Performance: The median accuracy appears higher for models trained with weight decay, showcasing its potential benefit in stabilizing and improving validation performance.
Comparing AdamW to Other Optimizers
Adam vs. AdamW
The key difference lies in how weight decay is applied. While Adam applies decay indirectly through the loss function, AdamW applies it directly during parameter updates. This distinction may seem minor but leads to more reliable training dynamics.
In experiments, AdamW consistently outperforms Adam for tasks like:
- Fine-tuning transformers for NLP.
- Training deep convolutional networks for image classification.
SGD with Momentum vs. AdamW
SGD with momentum is another popular optimizer, especially for computer vision tasks. While it offers simplicity, it lacks the adaptive learning rate benefits of AdamW. For models requiring intricate updates, AdamW often edges ahead in performance.
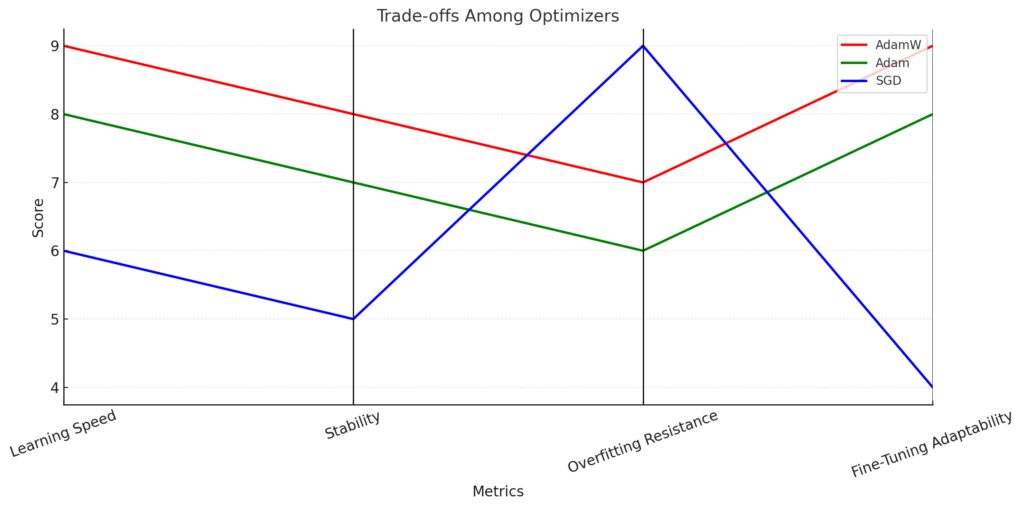
Stability: AdamW has a slight edge over Adam, with SGD trailing.
Overfitting Resistance: SGD outperforms the other optimizers significantly.
Fine-Tuning Adaptability: AdamW excels, followed by Adam, while SGD shows limitations.
The distinct lines in red, green, and blue represent the profiles of AdamW, Adam, and SGD, respectively. This visual clearly showcases their strengths and weaknesses for different use cases. Let me know if you’d like to refine or expand this visualization!
Key Tips for Using AdamW Effectively
Combine with Learning Rate Schedulers
Pair AdamW with schedulers like Cosine Annealing or Warm Restarts to maintain stability. These schedulers help fine-tune learning rates over time, complementing weight decay.
Monitor Training and Validation Metrics
To ensure optimal performance, closely monitor validation loss and accuracy during fine-tuning. A significant divergence may signal improper weight decay or learning rates.
Layer-Specific Weight Decay
Advanced practitioners often use layer-specific weight decay for transformers and large neural networks. Lower decay for early layers and higher for later ones can improve task-specific adaptation.
Real-World Success with AdamW
BERT and GPT Fine-Tuning
Modern NLP depends on pre-trained models like BERT and GPT, which are fine-tuned for tasks such as sentiment analysis, question answering, and summarization. AdamW enables these massive architectures to maintain their learned representations while adapting effectively to new tasks.
Vision Transformers (ViTs)
For computer vision, Vision Transformers (ViTs) have taken the spotlight. These models benefit greatly from AdamW’s ability to handle sparse updates, ensuring consistent training across large datasets.
Generative AI and Stable Diffusion
Generative models, including Stable Diffusion and GANs, leverage AdamW to fine-tune without sacrificing stability. Its weight decay ensures the generator and discriminator evolve cohesively, leading to sharper outputs.
Comparing AdamW with Other Optimizers and Techniques
AdamW vs. Adam
| Feature | Adam | AdamW |
|---|---|---|
| Weight Decay | Applied through loss function, indirectly affects gradients. | Decoupled from loss, applied directly to parameters. |
| Stability | Prone to overfitting in fine-tuning tasks due to inconsistent regularization. | More stable and consistent, especially for fine-tuning large models. |
| Training Dynamics | Irregular updates, particularly for sparse gradients. | Smoother updates, better suited for sparse gradients. |
| Performance | Often inferior on fine-tuned tasks or with small datasets. | Superior, especially for pre-trained transformer or vision models. |
Example: Fine-tuning a transformer:
Adam may yield fluctuating loss curves, while AdamW ensures a steady convergence trajectory.
AdamW vs. SGD with Momentum
| Feature | SGD with Momentum | AdamW |
|---|---|---|
| Learning Rate | Requires careful tuning; less adaptive. | Adaptive learning rate, simplifies hyperparameter selection. |
| Weight Decay | Applied directly, similar to AdamW. | Applied directly, but with adaptive learning advantages. |
| Speed | Slower convergence due to fixed learning rate schedule. | Faster convergence, especially for complex architectures. |
| Use Cases | Ideal for small models or large-scale vision tasks. | Excellent for fine-tuning large, pre-trained models. |
Example: Training ResNet on ImageNet:
SGD excels for pure image classification tasks, while AdamW is better suited for fine-tuning vision transformers (ViTs).
AdamW vs. RMSProp
| Feature | RMSProp | AdamW |
|---|---|---|
| Weight Decay | Not explicitly supported, must be added manually. | Integrated directly into the optimizer. |
| Learning Rate | Adaptive but sensitive to hyperparameters. | More stable adaptation and easy to tune. |
| Performance | Suitable for recurrent models (e.g., LSTMs). | Superior for transformers, CNNs, and large-scale tasks. |
| Stability | Can be unstable for large architectures. | Highly stable, especially for fine-tuning. |
Example: RMSProp may work well for training smaller RNN-based models, but AdamW is preferred for transformers like BERT or GPT.
Weight Decay vs. Dropout
| Feature | Weight Decay | Dropout |
|---|---|---|
| Mechanism | Penalizes large parameter values, keeping the model compact. | Randomly drops neurons during training. |
| Overfitting | Controls overfitting by limiting parameter growth. | Prevents co-adaptation of neurons. |
| Best Use Case | Effective for dense models, like transformers and CNNs. | Useful in shallow networks or for boosting generalization in fully connected layers. |
| Combination | Can be combined with dropout for robust regularization. | Often paired with weight decay for better performance. |
Example: Combining weight decay and dropout:
model = nn.Sequential(
nn.Linear(768, 512),
nn.Dropout(0.2), # Dropout to prevent co-adaptation
nn.ReLU(),
nn.Linear(512, 10),
)
optimizer = AdamW(model.parameters(), lr=3e-4, weight_decay=0.01)
AdamW vs. LARS (Layer-wise Adaptive Rate Scaling)
| Feature | LARS | AdamW |
|---|---|---|
| Learning Rate | Scales learning rates per layer for large batch training. | Uses adaptive learning rates, suitable for standard batch sizes. |
| Weight Decay | Explicitly included but designed for very large models. | Handles regularization more broadly and flexibly. |
| Best Use Case | Training massive models with very large batch sizes (e.g., distributed systems). | Fine-tuning pre-trained models or standard deep learning tasks. |
Example: LARS is typically used in large-scale distributed setups like training GPT models from scratch, while AdamW dominates fine-tuning tasks.
Which Optimizer Should You Use?
- Choose AdamW for:
- Fine-tuning large pre-trained models like BERT or Vision Transformers (ViTs).
- Tasks requiring adaptive learning rates (e.g., NLP or computer vision).
- Sparse gradient scenarios, where updates are uneven across layers.
- Choose SGD with Momentum for:
- Image classification tasks with smaller, convolution-based models (e.g., ResNet).
- Simpler tasks where adaptive learning isn’t as crucial.
- Choose RMSProp for:
- Recurrent models like LSTMs or GRUs, where RMSProp’s stability with sequence data is beneficial.
FAQs
What is the difference between weight decay and L2 regularization?
Weight decay and L2 regularization are closely related but differ in implementation.
In L2 regularization, the penalty term is added to the loss function. This means the optimizer indirectly applies the penalty by modifying the gradients during backpropagation.
Weight decay, on the other hand, directly adjusts the weights during the optimizer’s parameter update step, independent of the loss calculation.
Example:
Using AdamW for weight decay:
optimizer = AdamW(model.parameters(), lr=5e-5, weight_decay=0.01)
Why does AdamW improve fine-tuning stability?
AdamW improves stability by decoupling weight decay from the learning rate adjustment. This separation ensures that the optimizer applies weight decay consistently across updates without distorting the gradient-based learning process.
In fine-tuning scenarios, where small datasets are common, this stability reduces the risk of overfitting and erratic loss curves.
Example: Fine-tuning BERT for sentiment analysis:
optimizer = AdamW(model.parameters(), lr=3e-5, weight_decay=0.01)
How do I choose the best weight decay value?
The ideal weight decay depends on your model and dataset. Start with default values like 0.01 for most applications. For smaller datasets, you may want to lower it to avoid underfitting.
Tip: Use a grid search to systematically try multiple values (e.g., 0.001, 0.01, 0.1). Monitor validation loss for over-regularization (high bias) or under-regularization (high variance).
Can I use AdamW with learning rate schedulers?
Yes, AdamW pairs well with learning rate schedulers. Combining them helps fine-tune learning rates dynamically during training, improving both convergence and model performance.
Example: Using a linear decay scheduler with AdamW:
from transformers import get_scheduler
scheduler = get_scheduler(
"linear", optimizer=optimizer, num_warmup_steps=0, num_training_steps=num_steps
)
Is AdamW suitable for all models?
AdamW is versatile but not always the best choice for all scenarios. It excels with large pre-trained models (e.g., BERT, ResNet) and in fine-tuning tasks. For smaller models or datasets, simpler optimizers like SGD with momentum may perform adequately.
Example: Training ResNet with AdamW for CIFAR-10:
optimizer = AdamW(model.parameters(), lr=1e-4, weight_decay=0.01)Why does decoupling weight decay from the loss function matter?
Decoupling weight decay ensures that the penalty applies directly to the model’s parameters rather than through gradients derived from the loss function. This distinction prevents undesired interactions between weight decay and learning rate adjustments, leading to more precise regularization.
In practice, decoupling enhances the optimizer’s ability to handle large pre-trained models like transformers, where stability and generalization are crucial.
Example: Adam vs. AdamW in fine-tuning BERT:
- Adam (without decoupling): May lead to uneven weight updates, affecting convergence.
- AdamW: Maintains stable weight updates, producing smoother training dynamics.
What is layer-wise weight decay, and when should I use it?
Layer-wise weight decay allows you to assign different decay values to different parts of the model. This technique is especially useful in fine-tuning large models like transformers, where early layers may require less regularization than task-specific layers.
Example: Fine-tuning BERT with custom weight decay:
parameters = [
{"params": model.bert.encoder.parameters(), "weight_decay": 0.01}, # Base layers
{"params": model.classifier.parameters(), "weight_decay": 0.0}, # Classifier head
]
optimizer = AdamW(parameters, lr=3e-5)
This setup ensures task-specific layers adapt more freely while base layers remain stable.
Can AdamW handle sparse gradients effectively?
Yes, AdamW handles sparse gradients well, making it ideal for models like transformers and large vision networks. Sparse gradients are common in tasks like NLP token classification or vision object detection, where certain parameters update less frequently.
By applying weight decay directly to the parameters, AdamW ensures that even sparse layers remain regularized, avoiding uncontrolled parameter growth.
What datasets benefit most from AdamW optimization?
AdamW is highly effective for:
- Text-based datasets:
- IMDb: Sentiment classification (binary).
- SQuAD: Question answering tasks.
- AG News: Multi-class text classification.
- Vision datasets:
- CIFAR-10: Image classification.
- ImageNet: Fine-tuning large-scale image recognition models.
- Multimodal datasets:
- MS COCO: Image captioning and object detection.
- CLIP data: Joint image-text embeddings.
How does weight decay compare to dropout for regularization?
Weight decay and dropout both prevent overfitting but operate differently:
- Weight Decay: Applies a penalty to parameter magnitudes, keeping weights small and improving generalization.
- Dropout: Randomly disables neurons during training, forcing the network to learn robust features.
For deep models like transformers, weight decay via AdamW often performs better, as it aligns naturally with gradient-based optimization. Dropout is still useful for preventing co-adaptation of neurons, but it’s typically used in tandem with weight decay.
Example: Combining AdamW with dropout:
import torch.nn as nn
model = nn.Sequential(
nn.Linear(768, 512),
nn.Dropout(0.1),
nn.ReLU(),
nn.Linear(512, 2),
)
optimizer = AdamW(model.parameters(), lr=5e-5, weight_decay=0.01)Resources
Official Documentation
- Hugging Face Transformers
Transformers Documentation – Optimizers
Detailed guide on using AdamW with pre-trained models for fine-tuning. Includes examples and scheduler integrations. - PyTorch Optimizer Docs
AdamW in PyTorch
Official PyTorch documentation for AdamW, including parameter details and example usage.
Research Papers
- AdamW Original Paper:
Decoupled Weight Decay Regularization
Read the Paper on arXiv
A foundational paper by Ilya Loshchilov and Frank Hutter explaining AdamW and its advantages over Adam. - Transformer Fine-Tuning:
Attention is All You Need
Read the Paper on arXiv
The seminal paper introducing the transformer architecture, where optimizers like AdamW are commonly used.
Open-Source Projects
- Fastai
Fastai GitHub Repository
A deep learning library with accessible implementations of AdamW and related techniques. - Transformers Library
Hugging Face Transformers GitHub
A robust library for fine-tuning models like BERT, GPT, and Vision Transformers with AdamW.
Academic Datasets for Practice
- Kaggle Datasets
Explore Kaggle
Search for datasets compatible with AdamW fine-tuning tasks, such as IMDb for NLP or CIFAR-10 for vision. - Hugging Face Datasets
Datasets Library
Access thousands of datasets for fine-tuning models, all integrated with the transformers ecosystem. - TensorFlow Datasets
TFDS Documentation
Offers a wide range of datasets like ImageNet, MNIST, and SQuAD for tasks using AdamW.