
Gradient descent is the backbone of many optimization techniques in machine learning, but it can falter with sparse data or high-variance scenarios. These two situations pose unique challenges.
With strategic adjustments, gradient descent can remain effective even under challenging data conditions.
Why Sparse Data and High Variance Cause Issues in Gradient Descent
Sparse data and high-variance scenarios make gradient descent harder to control and converge. Let’s look at why these conditions are difficult for traditional gradient methods.
Sparse Data Challenges
Sparse data is typically characterized by large numbers of zeros or missing values. It often appears in recommendation systems and natural language processing where high-dimensional datasets are common. Sparse datasets can disrupt gradient calculations and lead to sluggish or inaccurate updates.
Sparse datasets:
- Reduce the density of feature vectors, limiting the ability to learn from patterns.
- Cause computational inefficiencies due to many empty values.
- Often exacerbate issues with convergence, as the algorithm may not reach the minimum easily.
High-Variance Situations
High-variance data, meanwhile, can emerge from noisy measurements or highly volatile data sources. Gradient descent struggles here because:
- Gradient fluctuations can cause oscillations around the optimal point, slowing convergence.
- High variance can make it difficult to balance between fitting the data and overfitting noise, potentially leading to poor generalization.
- Learning rates may require more frequent adjustments to avoid overshooting or converging prematurely.
Techniques for Handling Sparse Data in Gradient Descent
When working with sparse data, a few gradient descent techniques can help improve performance and model reliability.
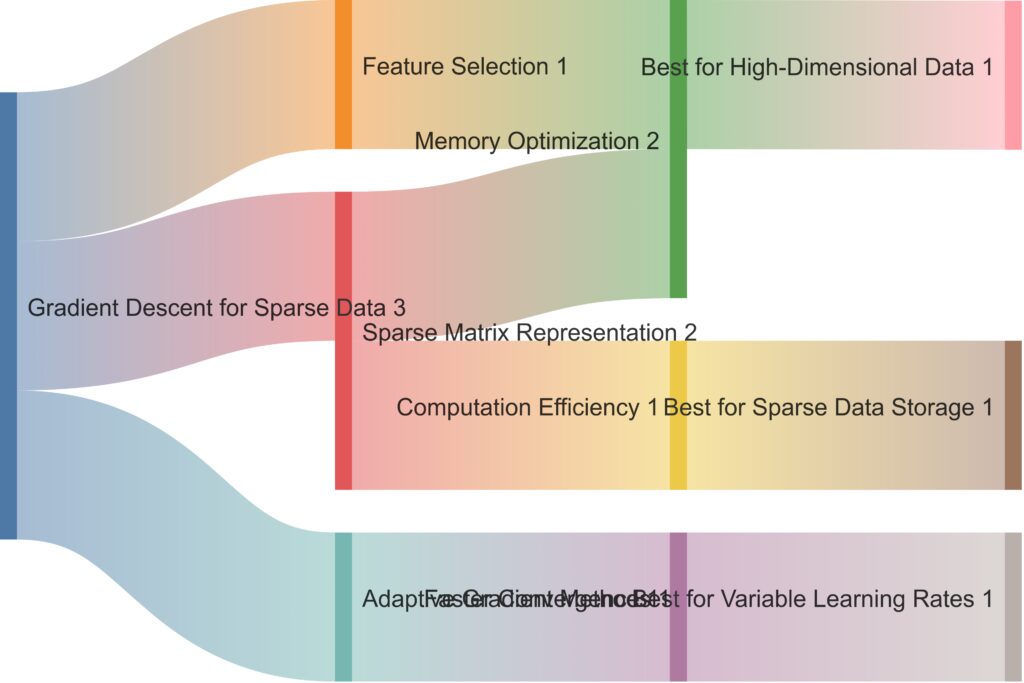
Feature Selection: Focuses on Memory Optimization, beneficial for high-dimensional data.
Sparse Matrix Representation: Enhances both Memory Optimization and Computation Efficiency, ideal for sparse data storage.
Adaptive Gradient Methods: Aims for Faster Convergence, suitable for scenarios requiring variable learning rates.
Each pathway highlights the role of these techniques in optimizing memory, computation, and convergence, showcasing the scenarios that best benefit from each method.
1. Sparse Matrix Representations
Use efficient sparse matrix formats to store and process data. Compressed Sparse Row (CSR) or Compressed Sparse Column (CSC) formats are common solutions to avoid memory overhead from zero values.
Benefits:
- Memory efficiency: Fewer resources are needed to store sparse data.
- Computational efficiency: Only non-zero entries are used in calculations, making gradient updates faster.
2. Feature Selection and Dimensionality Reduction
In sparse datasets, many features contribute little or no predictive value. Feature selection can eliminate these unnecessary features and allow gradient descent to operate on a reduced, more informative set.
Methods include:
- L1 regularization (Lasso): Encourages sparsity by pushing irrelevant feature coefficients to zero.
- Principal Component Analysis (PCA): Reduces dimensionality by finding directions of greatest variance, which can capture important features in a low-dimensional space.
3. Adaptive Gradient Methods
Adaptive methods like AdaGrad and Adam adjust the learning rate for each parameter individually. In sparse data contexts, this means that less frequently updated parameters (often those tied to non-zero values) get more attention.
Benefits:
- Efficient updates: Rarely updated parameters benefit from adaptive adjustments.
- Better convergence: Slows down updates for parameters linked to more common features, promoting stability.
Comparison of gradient descent techniques for sparse data
| Method | Key Features | Benefits for Sparse Data | Computational Efficiency | Convergence Behavior |
|---|---|---|---|---|
| Standard Gradient Descent | Basic update rule for each iteration. | Limited use for sparse data due to dense updates. | Low for large datasets; costly due to full dataset | Slow, can struggle with saddle points or local minima. |
| Proximal Gradient Descent | Adds proximal operator for sparsity control. | Excellent for sparse data, enforces sparsity in solutions. | Moderate, extra computations for proximal step. | Faster convergence by keeping updates within bounds. |
| Adaptive Gradient Methods | Adjusts learning rate per parameter (e.g., AdaGrad). | Helps manage sparse updates with varying learning rates. | Efficient, saves time on redundant updates. | Faster, adaptive rates help avoid poor local minima. |
| Mini-Batch Gradient Descent | Uses a subset of data for each update. | Indirectly benefits by improving generalization. | High, as it uses batches rather than full dataset. | Good convergence balance, smooths fluctuations. |
Sparse Benefits: Leaf icon for sparse data optimization.
Convergence: Downward arrow for improved convergence rate.
This table emphasizes each method’s unique strengths, particularly in handling sparse data, ensuring computational efficiency, and achieving faster convergence. Let me know if you’d like additional details or further customization!
Techniques for Gradient Descent in High-Variance Scenarios

High-variance data introduces unique problems, but with the right approach, you can maintain effective learning rates and reduce oscillations.
1. Stochastic Gradient Descent with Mini-Batches
In high-variance data, large batches can worsen variance by over-representing extreme values. Mini-batch gradient descent, however, balances between stability and efficiency by randomly sampling small subsets of data.
Advantages:
- Reduced variance: Mini-batches help smooth out noisy updates, leading to better convergence.
- Faster computation: Mini-batches lower computation time per update, often leading to more efficient training.
2. Learning Rate Schedulers
Dynamic adjustment of the learning rate during training can address issues of overshooting in high-variance settings. Schedulers, such as step decay or exponential decay, help adapt learning rates over time.
Types of learning rate schedules:
- Exponential decay: Gradually decreases the learning rate at a fixed rate.
- Cyclic learning rates: Alternate between low and high learning rates within a range, which can avoid getting stuck in local minima.
3. Momentum-Based Techniques
In high-variance scenarios, momentum-based methods smooth out fluctuations by considering past gradient directions. Algorithms like Nesterov Accelerated Gradient (NAG) leverage momentum but with a cautious approach to prevent overshooting.
Benefits of momentum:
- Reduced oscillations: Momentum methods dampen gradient oscillations, improving stability.
- Faster convergence: Accumulates useful gradients over time, guiding the model toward the optimal path.
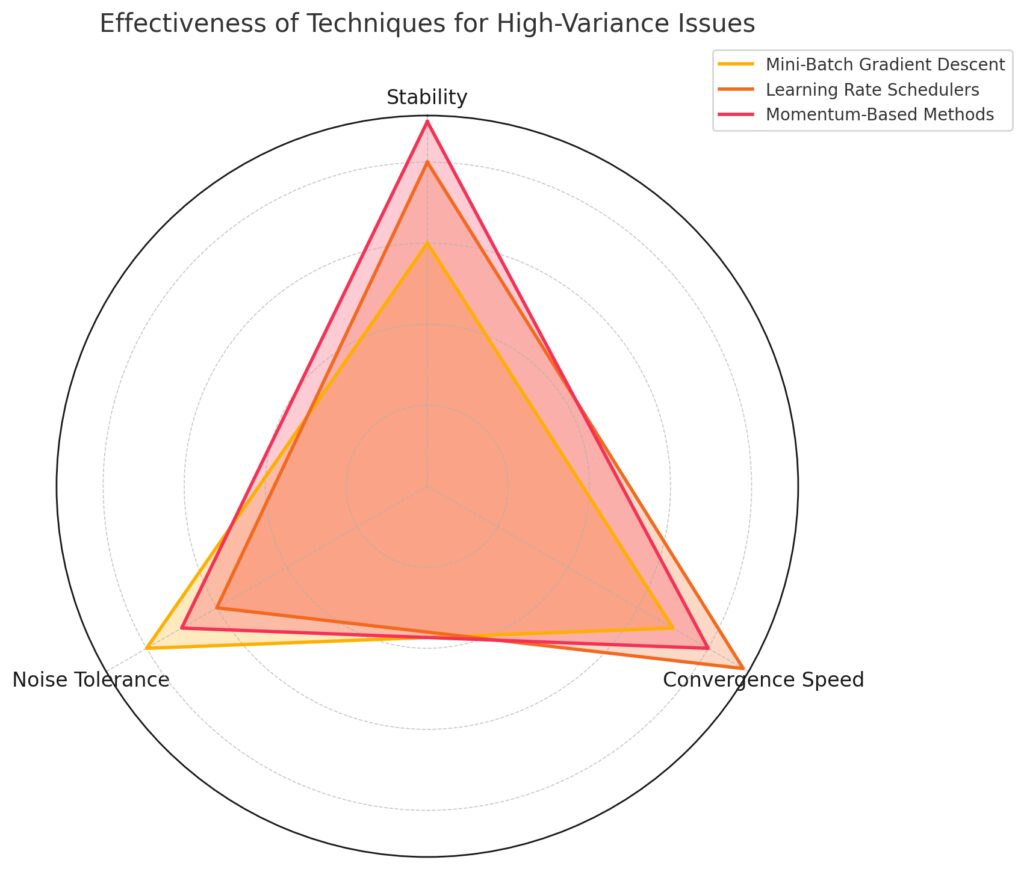
Mini-Batch Gradient Descent: Moderate stability, good convergence speed, and high noise tolerance.
Learning Rate Schedulers: High convergence speed and stability, with moderate noise tolerance.
Momentum-Based Methods: Highest stability, strong convergence speed, and good noise tolerance.
Combining Approaches for Robust Gradient Descent
Sparse data and high-variance situations are often present simultaneously, especially in fields like financial modeling or genomics. Here’s how to integrate the above techniques for optimal results.
Adaptive Mini-Batch Gradient Descent
Using mini-batches with adaptive learning rates can balance sparse data issues and high variance by maintaining stable and efficient updates across both non-zero and zero entries. Mini-batches ensure that gradients remain smooth, while adaptive adjustments help the model respond flexibly to sparse features.
Regularization with Adaptive Gradient Methods
Regularization methods like L1 (Lasso) or Elastic Net can work well with Adam or RMSprop, adding stability to sparse models while preventing extreme gradient updates. Elastic Net combines L1 and L2 regularization, helping to retain important features while controlling for noisy data points.
Cyclical Learning Rates with Momentum
Combining cyclical learning rates with momentum-based approaches (like NAG) balances exploration and exploitation. This combination ensures that high-variance gradients are smoothed over iterations without overshooting and missing out on local minima.
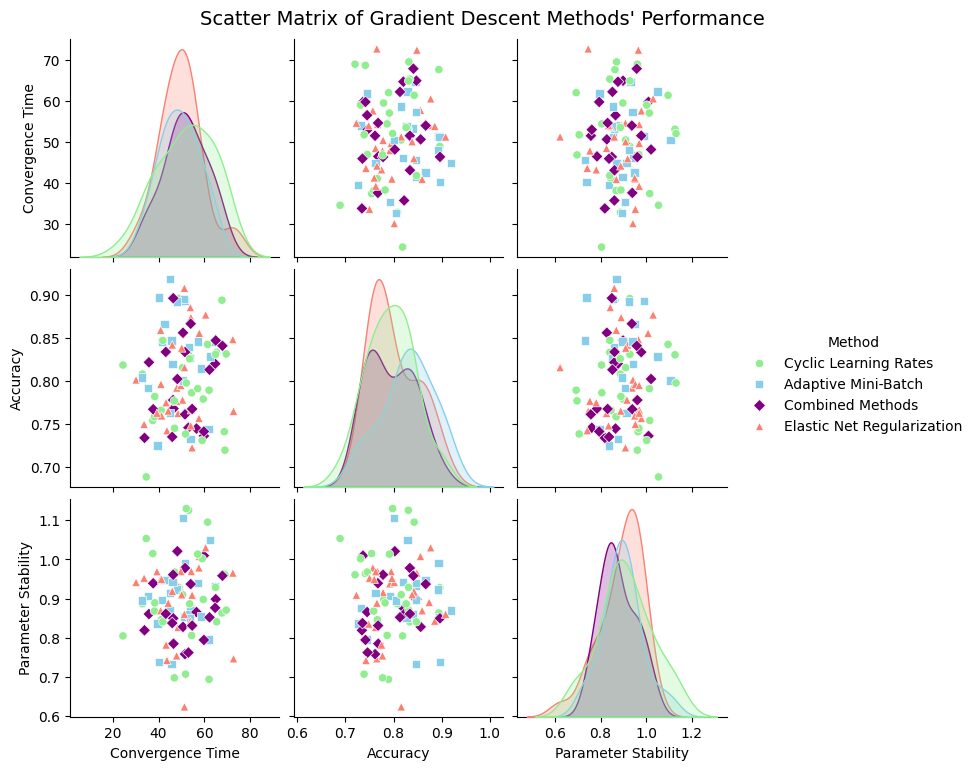
Axes: Convergence time on the x-axis and accuracy on the y-axis.
Color: Represents the method, with each technique color-coded.
Marker Style: Distinguishes dataset types (sparse vs. high variance).
This chart highlights the performance variations across techniques, helping visualize how each method adapts to different data challenges.
Advanced Strategies for Gradient Descent in Complex Scenarios
While basic gradient descent can struggle with sparse data and high variance, advanced strategies can enhance performance in these environments. Let’s explore methods like proximal gradient descent, regularization techniques, and variance reduction algorithms, which are particularly useful when standard adaptations aren’t enough.
Proximal Gradient Descent for Sparse Regularization

When dealing with sparse data, proximal gradient descent is highly effective, especially when used with L1 regularization. It integrates a “proximal operator” that applies a penalty to certain features, often driving coefficients of non-essential features to zero, which aligns well with sparse datasets.
How Proximal Gradient Descent Works
- Gradient Step: Proximal gradient descent starts with a standard gradient step on the objective function.
- Proximal Operator: Next, it applies a proximal operator, which pushes some parameters closer to zero, effectively enforcing sparsity.
This technique is particularly useful when paired with L1 regularization, making it ideal for high-dimensional data with sparse patterns (e.g., text data, gene expression data).
Advantages:
- Sparsity-friendly: Encourages sparse solutions by actively shrinking unimportant parameters.
- Computationally efficient: Requires fewer updates due to the proximal operator’s constraints, which speeds up training.
Use Cases for Proximal Gradient Descent
- Text classification: Sparse representations like TF-IDF vectors for natural language data.
- Feature selection tasks: High-dimensional spaces where only a small subset of features is relevant.
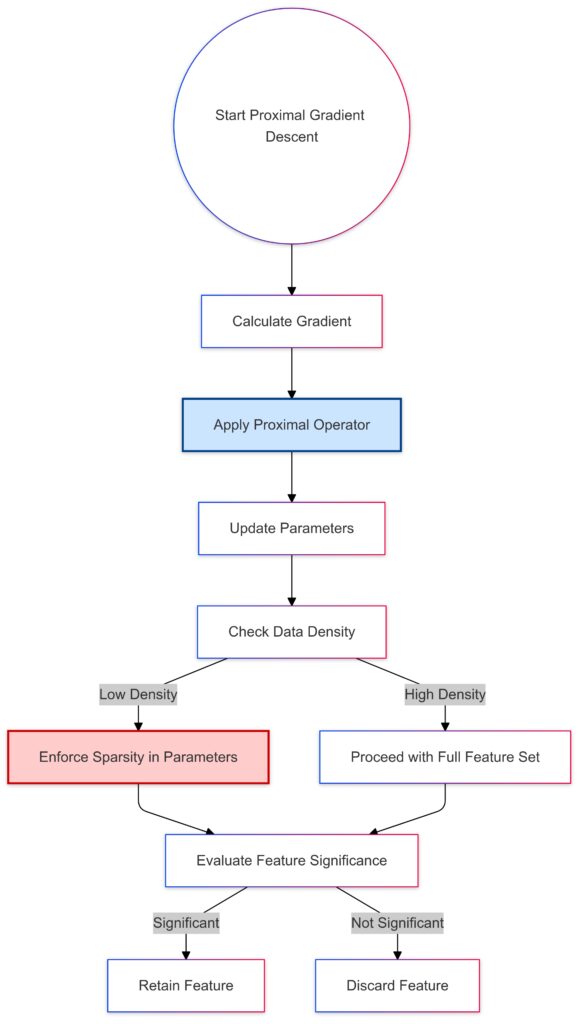
Gradient Calculation: Calculates the gradient based on current parameters.
Proximal Operator Application: Applies the proximal operator to introduce sparsity.
Parameter Update: Updates model parameters.
Data Density Check: Branches based on whether the data is sparse or dense:Low Density: Enforces sparsity in parameters.
High Density: Proceeds without sparsity constraints.
Feature Significance Evaluation: Determines if features should be retained or discarded.
This approach supports sparsity enforcement by adjusting feature sets based on data density and feature relevance.
Regularization Techniques to Stabilize Gradient Descent
In both sparse data and high-variance scenarios, regularization is a core tool to prevent overfitting and ensure smooth gradient updates. Different types of regularization can enhance stability and focus the model on relevant data patterns.
1. Elastic Net Regularization
Elastic Net combines L1 and L2 regularization. This blend offers both sparsity and stability, making it versatile for handling both sparse data and high variance.
- L1 (Lasso) term: Encourages sparsity by pushing small coefficients to zero.
- L2 (Ridge) term: Adds stability to the gradient updates, which is essential in noisy, high-variance data.
Elastic Net is effective in situations where you need a mix of both sparse feature selection and control over high variance, such as in recommendation systems or genetic data.
2. Dropout Regularization
Though more common in neural networks, dropout is another way to combat high variance. During each iteration, dropout randomly ignores a subset of nodes, which reduces the model’s sensitivity to specific data points and helps stabilize training.
Benefits of Dropout:
- Variance reduction: Helps control overfitting by reducing the model’s dependency on any single set of data points.
- Enhanced generalization: Encourages a robust model structure by training on random subsets of features.
Ideal for: Complex models that are highly susceptible to overfitting due to high-dimensional or noisy data, such as deep neural networks.
Variance Reduction Techniques in Stochastic Gradient Descent

In high-variance data environments, traditional Stochastic Gradient Descent (SGD) can be further optimized with variance reduction techniques like SVRG and SAGA.
Stochastic Variance Reduced Gradient (SVRG)
SVRG modifies standard SGD by periodically computing a more stable full gradient, which is then used to adjust mini-batch updates. This reduces the noise in each step and prevents the model from overreacting to individual samples, improving convergence.
How it works:
- Intermediate full gradient computation: Every few iterations, SVRG calculates a “snapshot” of the full gradient on the dataset.
- Adjusted mini-batch updates: Uses this snapshot to stabilize updates and keep SGD on track.
Benefits of SVRG:
- Better convergence rates: Stabilized updates allow faster convergence in high-variance scenarios.
- Noise control: Reduces the impact of outliers or noise in data.
SAGA Algorithm
SAGA improves on SVRG by further reducing variance with an element-wise storage of past gradient components, which enhances the model’s memory of past gradients.
Advantages:
- Memory efficiency: Keeps a history of gradient components for more accurate variance reduction.
- Improved stability: Particularly useful when there’s high variance in gradient updates due to noisy data.
Combining Gradient Techniques for Optimal Performance
Using a combination of these advanced techniques often brings the best results, especially in fields like natural language processing and financial data analysis, where sparse and high-variance data frequently overlap.
Proximal Gradient Descent with Variance Reduction
For extremely sparse datasets with high variance, combining proximal gradient descent with SVRG or SAGA can balance efficient convergence with sparse regularization. This approach can optimize gradient descent by targeting the most relevant features, ensuring stability, and controlling variance.
Elastic Net with Cyclic Learning Rates
In scenarios with high-dimensional and noisy data, Elastic Net paired with cyclic learning rates can provide strong regularization while adjusting the learning rate dynamically. This combination offers the advantage of exploring a range of values, which helps avoid local minima and improves generalization in complex datasets.
Final Thoughts: Tailoring Gradient Descent to Data Challenges
Sparse data and high variance both pose unique challenges, but with strategic adaptations, gradient descent can be tailored to overcome these issues. Whether through specialized methods like proximal operators or variance-reduction techniques, each adaptation strengthens gradient descent’s ability to find accurate solutions in tough scenarios.
When applying these methods, the key is to assess your dataset’s characteristics and test combinations that fit your data’s specific demands. This approach will ultimately lead to more reliable, efficient training, and better model performance.
FAQs About Gradient Descent for Sparse Data and High-Variance Scenarios
What is sparse data, and why does it affect gradient descent?
Sparse data is a type of dataset that contains many zero or missing values. In fields like natural language processing or recommender systems, sparse data is common because not every feature applies to every data point (e.g., word counts in text data or user-item interactions). Sparse data affects gradient descent by making gradient calculations less consistent and slowing down convergence. Gradient descent may struggle to find meaningful patterns due to the high number of zero values, leading to inefficient updates and longer training times.
How does high-variance data impact gradient descent?
High-variance data contains large fluctuations across samples, often due to noisy measurements or rapidly changing values. This variance can cause oscillations in gradient updates, leading the algorithm to “overshoot” the optimal point or get stuck. The challenge here is maintaining a learning rate that adapts to the dataset’s volatility without overfitting. In these cases, gradient descent may require techniques like mini-batches or momentum to stabilize and smooth out updates, resulting in more controlled convergence.
What is proximal gradient descent, and when should I use it?
Proximal gradient descent is a variant of gradient descent designed for problems with sparse regularization, such as those using L1 penalties. It applies a proximal operator that constrains certain parameters, pushing less relevant ones toward zero, which enforces sparsity in the solution. This technique is especially useful in high-dimensional datasets with many irrelevant features or in settings where model simplicity is crucial, as it reduces unnecessary complexity and improves interpretability.
How can adaptive gradient methods help with sparse data?
Adaptive gradient methods, like AdaGrad and Adam, adjust the learning rate for each parameter individually. In sparse datasets, this approach is beneficial because rarely updated parameters (those connected to non-zero entries) receive more focused attention. By updating each parameter at different rates, adaptive methods can make learning more efficient, resulting in better performance even when most features are absent or zero in the dataset.
What role does regularization play in high-variance data?
Regularization is crucial in high-variance scenarios because it prevents overfitting by penalizing overly complex models. Methods like L2 regularization (Ridge) and Elastic Net reduce the sensitivity of the model to individual noisy samples, which helps maintain stability in gradient descent. Elastic Net is particularly effective in high-variance environments, as it combines L1 and L2 regularization, encouraging feature selection while controlling for noise.
How does the SAGA algorithm reduce variance in gradient descent?
SAGA is a variance reduction algorithm that builds on stochastic gradient descent (SGD) by keeping a history of past gradient components. This method helps maintain stable updates even in noisy datasets by leveraging past information, reducing the randomness (variance) in gradient calculations. SAGA is especially helpful in large, high-variance datasets where typical SGD may struggle to converge due to fluctuations in gradient updates.
When should I use mini-batch gradient descent over full-batch or stochastic methods?
Mini-batch gradient descent is ideal for high-variance data because it balances the benefits of full-batch and stochastic gradient descent. It reduces variance by averaging gradients over a small subset of data, which helps stabilize updates and avoid the noisy fluctuations seen in purely stochastic methods. Mini-batches are particularly effective when you need fast yet stable training, as they allow for efficient updates and prevent the model from reacting too strongly to outliers in any single batch.
How can cyclical learning rates improve gradient descent for sparse and high-variance data?
Cyclical learning rates adjust the learning rate within a predefined range, allowing the model to explore different rates throughout training. This adjustment can prevent the model from getting stuck in local minima, which is useful in high-variance scenarios. By cycling through rates, the algorithm alternates between exploiting known patterns and exploring new parameter spaces, helping it find more robust solutions even with sparse or noisy data.
How does Elastic Net regularization compare to Lasso or Ridge in handling sparse data?
Elastic Net regularization combines the strengths of Lasso (L1) and Ridge (L2) regularization, making it more versatile. While Lasso promotes sparsity by pushing coefficients of irrelevant features to zero, Ridge prevents extreme parameter values by applying a quadratic penalty, which adds stability. In sparse data scenarios, Elastic Net encourages feature selection (like Lasso) while also maintaining model stability (like Ridge). This balance makes Elastic Net particularly useful when dealing with high-dimensional datasets where some features are sparse but also correlated, a scenario where Lasso alone might struggle.
What is the advantage of using momentum in high-variance gradient descent?
Momentum helps mitigate the effects of high-variance data by considering past gradients when updating parameters. This technique essentially adds a “velocity” component to the gradient descent, which helps to smooth out oscillations and avoid sudden jumps caused by noisy data points. By accumulating gradients over multiple steps, momentum-based methods like Nesterov Accelerated Gradient (NAG) can lead the model in a more stable direction. In high-variance scenarios, momentum reduces erratic behavior and accelerates convergence by maintaining a smoother trajectory.
Can gradient descent be used effectively with extremely sparse matrices?
Yes, gradient descent can be adapted to work effectively with sparse matrices by using sparse matrix representations (like CSR or CSC formats) and adaptive gradient methods. Sparse matrix formats allow for efficient storage and computation, as they avoid processing zero entries, reducing memory usage and computational load. Additionally, adaptive gradient methods focus learning on the non-zero elements, enabling gradient descent to progress more smoothly even with a high volume of zeros. For highly sparse data, combining these adaptations helps gradient descent achieve meaningful updates and faster convergence.
What are cyclic learning rates, and why do they work well with high-variance data?
Cyclic learning rates involve oscillating the learning rate between a minimum and maximum value during training. This method enables the model to alternate between exploration and exploitation, making it less likely to get stuck in local minima. For high-variance data, cyclic learning rates can be particularly useful because they allow for exploration in noisy or volatile data, helping the model to move past noise-driven suboptimal solutions. The oscillation also prevents premature convergence, which is essential in scenarios where the data has fluctuating patterns.
How does SVRG differ from standard SGD in handling high-variance data?
Stochastic Variance Reduced Gradient (SVRG) differs from standard Stochastic Gradient Descent (SGD) by calculating a full gradient snapshot periodically and using this to guide mini-batch updates. In high-variance data, standard SGD can produce noisy and inconsistent updates, which can slow down convergence. SVRG’s full gradient snapshot acts as an anchor, reducing the variance in mini-batch updates. This leads to more stable and controlled learning, allowing SVRG to converge faster than SGD in noisy environments without compromising the efficiency of mini-batch updates.
When should I prefer proximal gradient descent over standard gradient descent?
Proximal gradient descent is preferable in settings where sparse solutions are desired or necessary, such as high-dimensional feature spaces with many irrelevant features. The proximal operator in this method applies regularization, which encourages sparsity by shrinking less important parameters toward zero. This feature makes proximal gradient descent particularly effective in fields like text mining or genetic analysis, where high-dimensional data often has sparse patterns. Standard gradient descent, in contrast, does not inherently handle sparsity as effectively and may lead to slower convergence in these cases.
Can dropout regularization be used outside of neural networks?
Yes, dropout regularization can be adapted for use outside of neural networks, though it’s most commonly associated with them. In linear models, for instance, dropout can be implemented by randomly omitting features or parameters during each iteration, which helps prevent overfitting. In high-variance data, dropout can also reduce sensitivity to outliers by training the model on different subsets of data at each step. Although it’s not as common outside of neural networks, dropout can still provide benefits by improving generalization and enhancing robustness to noise.
What types of problems benefit most from variance reduction techniques like SAGA?
Variance reduction techniques like SAGA are particularly beneficial in large-scale machine learning problems with high-dimensional and noisy data, such as financial forecasting or recommendation systems. In these applications, variance reduction stabilizes updates, making it easier to train on vast datasets without succumbing to noise-driven instability. SAGA’s element-wise memory of past gradients is especially useful when data points vary significantly, as it helps maintain consistent gradient directions, leading to faster and more reliable convergence in complex environments.
Is mini-batch gradient descent always better than full-batch or stochastic methods?
Not necessarily. While mini-batch gradient descent offers a good balance between computational efficiency and gradient stability, the choice depends on the data and problem at hand. For small datasets, full-batch gradient descent may work well, as it computes gradients across the entire dataset, ensuring stable updates. In high-variance data, mini-batch is usually preferred to reduce oscillations without the high computational cost of full-batch methods. However, in highly noisy, sparse, or large-scale data, mini-batches help stabilize training, making it a popular choice for many modern applications.
Resources for Learning More About Gradient Descent, Sparse Data, and High Variance
Books
- “Deep Learning” by Ian Goodfellow, Yoshua Bengio, and Aaron Courville
This comprehensive textbook covers the foundations of gradient descent and its variations, including optimizations like adaptive methods and regularization. Chapter 8 delves into optimization algorithms, with a detailed look at handling high variance in training. - “Pattern Recognition and Machine Learning” by Christopher M. Bishop
This classic machine learning book covers key methods for dealing with high-dimensional and sparse data, and provides insights into regularization, optimization, and variance reduction techniques. - “The Elements of Statistical Learning” by Trevor Hastie, Robert Tibshirani, and Jerome Friedman
Widely regarded as a foundational text for statistical learning, this book covers a range of methods including L1 and L2 regularization, feature selection, and techniques for dealing with high-variance data. Chapter 3 is particularly relevant to gradient-based optimization in high-dimensional spaces.
Research Papers
- “Adam: A Method for Stochastic Optimization” by Diederik P. Kingma and Jimmy Ba
This paper introduces the Adam optimizer, which has become popular for adaptive learning in both sparse and high-variance scenarios. The authors explain how Adam dynamically adjusts learning rates, a feature that is particularly helpful in sparse datasets.
Link: Adam: A Method for Stochastic Optimization - “Stochastic Variance Reduced Gradient (SVRG) for Optimization” by Johnson and Zhang
This paper presents the SVRG algorithm, an effective approach for variance reduction in stochastic gradient descent, especially suited for noisy, high-variance datasets.
Link: Accelerating Stochastic Gradient Descent using Predictive Variance Reduction - “Regularization and Variable Selection via the Elastic Net” by Zou and Hastie
This seminal paper explains the Elastic Net regularization method, which combines L1 and L2 penalties to handle both feature selection and variance reduction.
Link: Elastic Net Regularization
Online Courses
- Coursera: “Machine Learning” by Andrew Ng
This course is an excellent starting point for understanding gradient descent, variance, and regularization. It covers essential techniques in handling sparse data and high variance, with practical examples in linear and logistic regression.
Link: Machine Learning by Andrew Ng - DeepLearning.AI: “Deep Learning Specialization”
This specialization, led by Andrew Ng, dives into gradient-based optimization in neural networks, including adaptive methods, regularization techniques, and handling sparse data in deep learning applications.
Link: Deep Learning Specialization - Fast.ai: “Practical Deep Learning for Coders”
Known for its practical, hands-on approach, Fast.ai’s course covers advanced optimization techniques in deep learning, including momentum, adaptive learning rates, and how to tackle high-variance and sparse data challenges.
Link: Practical Deep Learning for Coders
Online Articles and Blogs
- “A Gentle Introduction to Mini-Batch Gradient Descent and How to Configure Batch Size” by Jason Brownlee
This article explains the advantages of mini-batch gradient descent, a useful technique for controlling variance in gradient updates. Jason Brownlee’s blog is a reliable source for machine learning explanations with practical guidance. - “Explaining Regularization: L1 vs. L2 vs. Elastic Net” on Towards Data Science
This blog post provides a beginner-friendly overview of regularization techniques, comparing L1, L2, and Elastic Net, along with their application in handling sparse data. - “Adaptive Learning Rates: Adagrad, RMSprop, and Adam” on OpenAI Blog
This article offers an in-depth look at adaptive gradient methods, discussing why they work well with sparse and high-variance data. It includes visual examples and practical tips on when to use each technique.
Link: Adaptive Learning Rates
Tools and Libraries
scikit-learn Documentation
The scikit-learn library offers tools for gradient-based optimization, regularization (including Elastic Net), and feature selection. Its extensive documentation and user guides are excellent for understanding how to implement these techniques in traditional machine learning workflows.
TensorFlow and PyTorch Documentation
Both TensorFlow and PyTorch offer built-in implementations of advanced optimizers like Adam, AdaGrad, and RMSprop. Their documentation includes usage guidelines, making it easier to apply these techniques to real-world problems.