Kernel Density Estimation (KDE) is a versatile, non-parametric method for estimating the probability density function (PDF) of a random variable. If you’re dealing with complex or unknown distributions, KDE is your go-to tool.
This article dives into its mechanics, practical applications, and the nuances of bandwidth selection.
What is Kernel Density Estimation?
A Glimpse into Non-Parametric Methods
Unlike parametric methods that assume a specific distribution (e.g., Gaussian), non-parametric approaches like KDE make no such assumptions. Instead, KDE creates a smooth estimate of the data’s PDF by summing contributions from every data point.
- Imagine plotting a histogram but replacing the rigid bins with smooth, overlapping curves.
- This flexibility makes KDE ideal for exploring data without prior distribution knowledge.
Breaking Down the KDE Formula
At its core, the KDE formula looks like this:
[math]\hat{f}(x) = \frac{1}{n h} \sum_{i=1}^n K\left(\frac{x – x_i}{h}\right) [/math]
Here’s what it all means:
- nnn: Number of data points.
- hhh: Bandwidth (a smoothing parameter).
- KKK: Kernel function (defines the shape of each curve).
In plain terms, KDE sums up scaled contributions from kernel functions centered at each data point.
Why is Bandwidth Crucial in KDE?
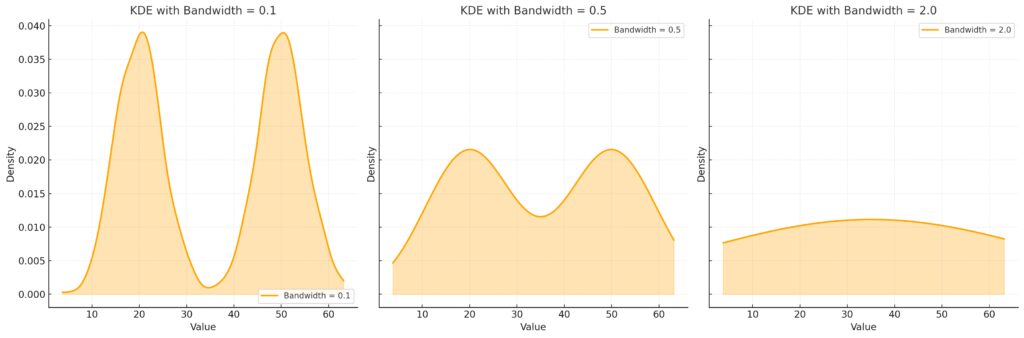
Effect: Overfitting the data.
Characteristics: Captures every minor fluctuation, leading to a noisy and jagged estimate.
Drawback: Hard to discern the overall distribution.
Optimal Bandwidth (0.5):
Effect: Balanced representation.
Characteristics: Smoothly captures the bimodal nature of the data, with distinct peaks for dense regions.
Benefit: Provides an accurate and interpretable estimate.
Large Bandwidth (2.0):
Effect: Oversmoothing the data.
Characteristics: The two peaks merge into a single broad curve, losing detail in the distribution.
Drawback: Misses the multimodal structure.
Balancing Smoothness and Detail
The bandwidth (h) determines the width of the kernel functions, controlling how smooth or detailed the density estimate appears.
- Small hhh: High detail, potentially too much noise.
- Large hhh: Smoother curves, but risk of oversimplification.
Choosing the right bandwidth is critical, as it directly impacts the accuracy of your estimate.
Methods for Bandwidth Selection
- Rule of Thumb: Quick but less adaptive. Uses formulas based on data variance.
- Cross-Validation: Optimizes hhh by minimizing error.
- Plug-In Methods: Automated approaches that work well in practice.
Kernel Functions: The Heart of KDE
Common Types of Kernels
Kernels are the building blocks of KDE. They dictate how data points contribute to the density estimate.
- Gaussian Kernel: Smooth and widely used.
- Epanechnikov Kernel: Computationally efficient.
- Uniform Kernel: Simplest but less common.
Each kernel integrates to 1, ensuring the resulting curve represents a proper probability density.
When to Choose Different Kernels
While the Gaussian kernel is the default for most applications, other kernels might be better suited depending on your data’s shape or computational needs. Fortunately, the kernel choice often has less impact than bandwidth selection.
Applications of Kernel Density Estimation
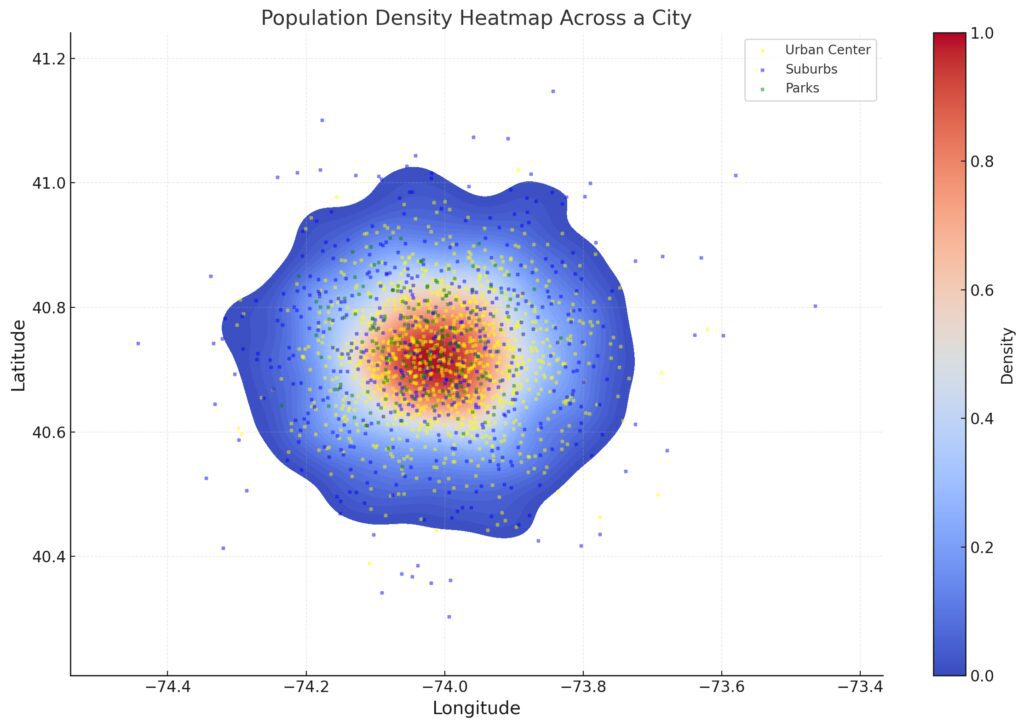
High-Density Areas (Urban Centers):
- Clearly marked in bright yellow regions, representing the central urban zones with high population density.
Low-Density Zones (Suburbs and Parks):
- Suburbs: Shown in cooler colors (blue), indicating moderate population density.
- Parks: Highlighted in green, representing sparsely populated areas.
Color Gradient: The heatmap’s color gradient (from blue to red) emphasizes variations in density, with warmer colors indicating higher densities.
Visualizing Data Distributions
One of the most common uses of KDE is visualizing data distributions. Unlike histograms, which depend on bin placement and size, KDE provides a smooth and continuous representation of the data.
- Ideal for exploratory data analysis (EDA) to uncover hidden patterns.
- Helpful in comparing multiple distributions on the same axis.
For instance, plotting KDEs for multiple groups in a dataset can reveal overlaps or differences more effectively than histograms.
Density-Based Clustering and Outlier Detection
KDE is central to density-based clustering methods, like DBSCAN, where regions of high density define clusters.
- Detect outliers in low-density areas.
- Identify sub-populations within complex datasets.
By evaluating the density at different points, you can pinpoint regions that deviate significantly from expected patterns.
Applications in Machine Learning
KDE has found its way into machine learning and statistics for tasks such as:
- Feature Engineering: Capturing data spread as additional features.
- Anomaly Detection: Recognizing low-probability regions as anomalies.
- Bayesian Inference: Using KDE to approximate priors or likelihoods.
In practice, KDE often complements other tools, filling gaps where parametric models fall short.
Strengths and Limitations of KDE
Advantages of Using KDE
- Flexibility: No assumptions about the underlying distribution.
- Visualization Power: Intuitive, smooth, and easy to interpret.
- Adaptable Bandwidths: Adjust for local or global density estimates.
These benefits make KDE a versatile tool across multiple domains, from biology to finance.
Challenges and Trade-Offs
- Computational Intensity: Large datasets require more processing due to the sum over all points.
- Bandwidth Sensitivity: Incorrect bandwidth can lead to over- or under-smoothing.
- Boundary Effects: KDE struggles near data boundaries unless corrected.
Despite these limitations, KDE remains a gold standard for non-parametric density estimation when used with care.
How to Implement KDE in Python
Popular Libraries for KDE
Python offers several libraries to implement KDE seamlessly:
- Scipy: Built-in function
gaussian_kdefor simple use cases. - Seaborn: Generates visually appealing KDE plots with
sns.kdeplot. - Statsmodels: Provides advanced options for customization.
Each library has strengths depending on whether your focus is visualization or computation.
Example Code for KDE
Here’s a simple implementation using Python:
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
# Generate sample data
data = np.random.normal(0, 1, 1000)
# Plot KDE
sns.kdeplot(data, bw_adjust=0.5, fill=True)
plt.title("KDE of Sample Data")
plt.xlabel("Value")
plt.ylabel("Density")
plt.show()
This example uses Seaborn to create a smooth density estimate with adjustable bandwidth (bw_adjust).
Enhancing KDE for Advanced Use Cases
Adaptive Bandwidth for Varying Densities
In some datasets, the density of points varies significantly. A fixed bandwidth may oversmooth dense areas or undersmooth sparse ones. Enter adaptive KDE, which adjusts the bandwidth based on local data density:
- Smaller bandwidth in dense regions ensures detail.
- Larger bandwidth in sparse areas avoids noise.
Adaptive methods improve accuracy, especially in multi-modal distributions.
Multivariate KDE for Higher Dimensions
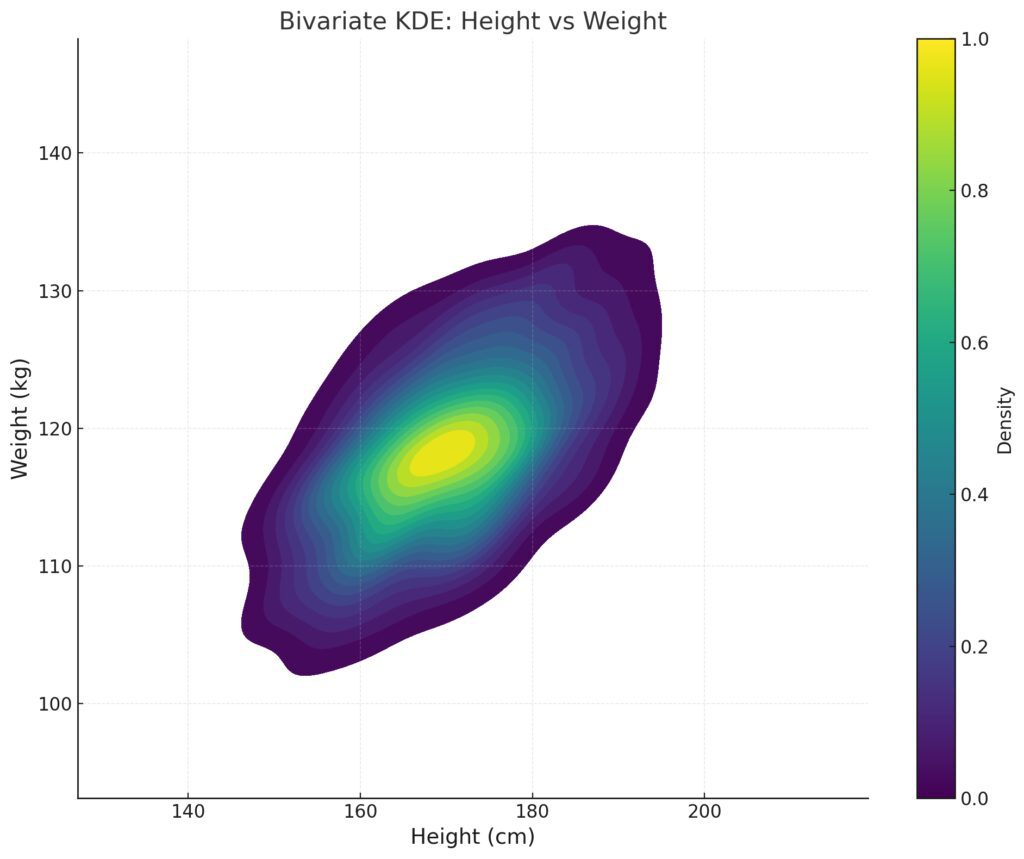
Color Gradient: Highlights density variations, with brighter regions indicating higher joint density.Contours: Represent density levels, helping to pinpoint regions where height and weight values are more likely to occur together.Dataset Characteristics: The density peaks around the center of the distribution, reflecting the correlation between height and weight.
While most examples focus on univariate data, KDE is highly effective in multivariate settings. Here, the kernel function operates in multiple dimensions, providing a joint probability density estimate.
- Ideal for understanding relationships between variables.
- Visualizing results often requires advanced techniques, like 3D plotting or contour maps.
However, beware of the curse of dimensionality—KDE can struggle as dimensions increase, making feature selection critical.
Boundary Correction Techniques

Issue: Density “leaks” beyond the boundaries, producing unrealistic estimates near 0 and 100.
Effect: Poor representation of density at boundary regions.
Reflection Method KDE (Middle):
Improvement: Reflects the data around boundaries, compensating for boundary bias.
Effect: Smooths density estimates near the edges while preserving the overall distribution shape.
Truncated Kernel KDE (Right):
Improvement: Forces density to zero outside the boundaries using truncated kernels.
Effect: Provides accurate density estimates within the bounds but introduces sharp drops at the edges.
KDE often underestimates densities near the boundaries of data, as kernel functions “spill over” beyond the observed range. To address this:
- Reflection Method: Reflects data points near boundaries to maintain density balance.
- Truncated Kernels: Adjusts kernels to fit within the boundary limits.
- Boundary Bias Adjustments: Directly modifies density calculations near edges.
These corrections are crucial for datasets with hard boundaries, such as geographic data or constrained measurements.
Real-World Applications of KDE
Finance: Modeling Asset Returns
KDE is widely used in finance to model asset return distributions, especially for non-normal data.
- Identifies heavy tails in stock return distributions.
- Supports Value at Risk (VaR) calculations by estimating probabilities of extreme losses.
Healthcare: Analyzing Medical Data
In healthcare, KDE helps in diagnostic modeling and disease pattern analysis:
- Maps patient densities geographically to identify outbreak hotspots.
- Estimates survival rates in non-parametric survival analysis.
The flexibility of KDE ensures that insights aren’t limited by rigid distributional assumptions.
Astronomy: Stellar Distribution Mapping
Astronomers rely on KDE to map stellar distributions in galaxies or estimate cosmic ray fluxes. KDE’s adaptability is invaluable for analyzing sparse but high-dimensional data in space.
Final Thoughts on Kernel Density Estimation
Kernel Density Estimation is a cornerstone of non-parametric analysis. With proper bandwidth selection and kernel choice, KDE becomes a powerful tool for understanding data distributions in almost any domain.
Whether you’re an analyst exploring data visually or a machine learning practitioner building density-based models, KDE offers the flexibility and precision you need.
FAQs
What are the common kernel functions used in KDE?
KDE uses various kernel functions, each shaping how data contributes to the density estimate. Common kernels include:
- Gaussian: Produces smooth, bell-shaped curves (most common).
- Epanechnikov: Computationally efficient, resembling a parabola.
- Uniform: Assigns equal weight within a fixed range (less common).
Example:
For most general-purpose applications, the Gaussian kernel is the default choice as it ensures smooth transitions across data points.
Why is bandwidth so important in KDE?
The bandwidth determines the smoothness of the KDE curve. It’s a critical parameter that directly affects the balance between bias and variance:
- Small bandwidth captures fine details but may introduce noise.
- Large bandwidth smooths the curve but risks oversimplifying the data.
Example:
In a dataset of monthly rainfall, a small bandwidth may show individual rainy days within each month, while a larger bandwidth provides a general view of seasonal trends.
How do I choose the right bandwidth?
There are several methods for bandwidth selection:
- Silverman’s Rule of Thumb: Quick and effective for unimodal data.
- Cross-Validation: Finds the bandwidth minimizing the error of the density estimate.
- Plug-In Methods: Automated approaches that adapt well to multimodal distributions.
Example:
For complex datasets with multiple peaks, cross-validation is often the most reliable method, while Silverman’s rule is faster for simpler cases.
What are the limitations of KDE?
While powerful, KDE has some limitations:
- Computational Intensity: Summing kernels for large datasets can be slow.
- Boundary Effects: Density estimates can drop near data boundaries.
- Curse of Dimensionality: Performance degrades with high-dimensional data.
Example:
If you’re estimating the density of a dataset representing geographic locations, KDE might underestimate points near the edges unless boundary correction is applied.
Can KDE be used for multivariate data?
Yes, KDE works with multivariate data, estimating joint densities for multiple variables. However, it becomes computationally challenging as the number of dimensions increases.
Example:
To study the relationship between height and weight, a 2D KDE could show a contour map highlighting areas of high joint density (e.g., clusters of people with similar height and weight).
How does KDE handle skewed data?
KDE can adapt to skewed data using adaptive bandwidth methods, which vary the bandwidth based on local data density. This ensures that dense areas get detailed smoothing, while sparse areas avoid overfitting.
Example:
In income distribution analysis, where most values cluster around a median but a few are extremely high, adaptive bandwidth KDE highlights both the cluster and the long tail effectively.
What tools can I use to implement KDE?
KDE is supported by many libraries and tools across programming languages:
- Python: Use
seaborn.kdeplot,scipy.stats.gaussian_kde, orstatsmodels. - R: The
densityfunction is a standard implementation. - MATLAB: Built-in functions like
ksdensity.
Example:
To visualize KDE in Python, you can use:
import seaborn as sns
sns.kdeplot(data, bw_adjust=0.5, fill=True)
This produces a smooth density plot with adjustable bandwidth.
How does KDE compare to parametric methods?
Parametric methods assume a specific distribution (e.g., normal), while KDE does not. KDE is more flexible but requires careful bandwidth selection.
Example:
If you’re analyzing heights and assume they follow a normal distribution, a parametric method would work. But for complex data (e.g., ages in a mixed population), KDE is better since it adapts to the actual shape.
How does KDE handle data boundaries?
KDE may underestimate densities near boundaries because the kernels extend beyond the dataset’s range. This is known as the boundary effect. Techniques to address this include:
- Reflection Method: Reflects data points near boundaries to balance the density estimate.
- Truncated Kernels: Modifies kernels to stop at boundaries.
- Data Transformation: Transforms data (e.g., logarithmic) to fit within valid boundaries.
Example:
For non-negative data like income, KDE might show artificially low density near zero unless boundary correction is applied.
Is KDE sensitive to outliers?
Yes, outliers can significantly influence KDE because every data point contributes to the overall density. However, this sensitivity depends on the bandwidth and kernel type:
- A smaller bandwidth will exaggerate the influence of outliers.
- Robust kernels (like Epanechnikov) can reduce the impact of outliers.
Example:
In a dataset of house prices, a single multimillion-dollar property could create a misleading bump in the density curve unless handled with an appropriate kernel or bandwidth.
Can KDE estimate probabilities for specific ranges?
Yes, KDE estimates a probability density function (PDF), which can be integrated to calculate the probability of a specific range. For instance, the probability of a random variable falling between aaa and bbb can be calculated as:
[math]P(a \leq X \leq b) = \int_{a}^{b} \hat{f}(x) \, dx
[/math]
Example:
If you’re analyzing exam scores, KDE could estimate the probability that a student scores between 70 and 80.
How does KDE compare to Gaussian Mixture Models (GMM)?
KDE and Gaussian Mixture Models (GMM) are both used for density estimation but differ in key ways:
- KDE: Non-parametric, smooths the density based on all data points.
- GMM: Parametric, assumes the data comes from a combination of Gaussian distributions.
Example:
KDE works well for general-purpose density estimation, but GMM is better for clustering tasks where distinct groups (e.g., customer segments) are expected.
What is the role of kernels in KDE?
The kernel function defines the shape of the curve used to estimate density around each data point. Kernels must satisfy these properties:
- Be symmetric.
- Integrate to 1 (ensures proper probability density).
- Have compact support (optional, for efficiency).
Example:
The Gaussian kernel assigns weights that decrease exponentially with distance, creating smooth and natural-looking curves.
What is adaptive KDE, and when is it useful?
Adaptive KDE adjusts the bandwidth for each data point based on local density. It uses smaller bandwidths in dense regions and larger ones in sparse regions.
Example:
If you’re analyzing city populations, adaptive KDE ensures detailed density in metropolitan areas while avoiding noise in rural regions.
How does KDE handle multimodal distributions?
KDE excels at estimating multimodal distributions because it doesn’t assume a single peak like parametric methods. Peaks naturally emerge from the data as long as the bandwidth is chosen correctly.
Example:
If analyzing website traffic, KDE can reveal separate peaks for weekday and weekend patterns, unlike a normal distribution, which would smooth them into one.
What are the limitations of multivariate KDE?
While multivariate KDE is powerful, it faces challenges:
- Curse of Dimensionality: As dimensions increase, data sparsity reduces the accuracy of KDE.
- Bandwidth Selection: Requires choosing a bandwidth for each dimension or a bandwidth matrix.
- Visualization: Harder to interpret in more than 3 dimensions.
Example:
For a 2D dataset of temperature and humidity, KDE works well to visualize joint density. But for 10 features, dimensionality reduction techniques like PCA are needed.
Can KDE be used for time-series data?
Yes, KDE can be applied to time-series data, but it works best for stationary data or snapshots in time. For dynamic changes, sliding windows or conditional KDE is more effective.
Example:
In stock price analysis, KDE can estimate the distribution of daily returns, but capturing trends over time requires additional methods.
How does KDE compare to parametric regression?
KDE is focused on estimating probability density, while parametric regression models relationships between variables. However, KDE can indirectly help regression tasks by estimating joint densities and deriving conditional probabilities.
Example:
If you’re modeling sales based on ad spend, KDE could estimate the joint density of both variables, helping identify relationships without assuming linearity.
Are there real-world scenarios where KDE excels?
KDE is highly versatile and finds applications in many fields:
- Finance: Estimating stock return distributions.
- Healthcare: Mapping disease hotspots geographically.
- Ecology: Analyzing animal movement patterns.
- Astronomy: Mapping the density of stars in galaxies.
Example:
Astronomers use KDE to detect clusters of stars or galaxies, revealing cosmic structures invisible with simpler methods.
Does KDE scale well for large datasets?
Scaling KDE for large datasets can be computationally expensive because each data point contributes to the density estimate. Optimization techniques include:
- Fast Fourier Transform (FFT): Speeds up convolution-based KDE.
- Tree-Based Algorithms: Partition data for faster kernel evaluations.
- Subsampling: Reduces the dataset size while preserving key patterns.
Example:
In processing billions of GPS points for traffic density analysis, FFT-based KDE significantly reduces computation time.
Resources for Learning and Applying Kernel Density Estimation
1. Foundational Articles and Tutorials
- Scikit-learn User Guide: Kernel Density Estimation
A practical introduction to KDE in Python using Scikit-learn, covering implementation and bandwidth selection techniques. - Statsmodels Documentation: KDE in Statsmodels
Detailed documentation for KDEUnivariate and its use for univariate density estimation in Python. - Towards Data Science: Understanding Kernel Density Estimation
A beginner-friendly explanation of KDE with clear visuals and Python examples.
2. Books for Deep Dives
- “Elements of Statistical Learning” by Hastie, Tibshirani, and Friedman
Chapter 6 provides a rigorous yet accessible treatment of density estimation, including KDE and its mathematical foundations.
Read Online (Stanford) - “Nonparametric Statistical Methods” by Myles Hollander and Douglas A. Wolfe
This comprehensive book explores non-parametric methods like KDE and their applications in real-world scenarios. - “Computer Age Statistical Inference” by Bradley Efron and Trevor Hastie
A modern look at statistical methods, including a section on KDE and its use in machine learning contexts.
3. Online Courses and Tutorials
- Coursera: “Statistical Inference and Modeling for High-throughput Experiments”
Offers a section on KDE and its use in experimental data modeling. Access here. - Datacamp: “Unsupervised Learning in Python”
Includes modules on density-based clustering and KDE. Access here. - YouTube Tutorials:
4. Research Papers and Case Studies
- Scott, D. W. (1992). “Multivariate Density Estimation: Theory, Practice, and Visualization.”
A highly regarded text for theoretical and practical applications of KDE. - “KDE-Based Anomaly Detection in Financial Transactions” (Springer)
Explores real-world applications of KDE in fraud detection.
5. Tools and Libraries
- Python Libraries:
seaborn.kdeplot: Simple KDE visualization.scipy.stats.gaussian_kde: Core implementation for flexible KDE.statsmodels.nonparametric.KDEUnivariate: Advanced options for univariate KDE.
- R Libraries:
density(): Core R function for KDE.ggplot2: Combine KDE with advanced plotting for beautiful visualizations.
- MATLAB:
- Use the built-in
ksdensityfunction for 1D and multivariate KDE.
- Use the built-in
6. Interactive Demos and Sandbox Tools
Shiny App for KDE in R
KDE Shiny App
Experiment with KDE parameters interactively in R.
Distill: Interactive Guide to KDE
Interactive KDE Demo
An interactive visual explainer to understand KDE and bandwidth effects.