Krylov Subspace: A Game-Changer For Quantum Computing

Enhancing Efficiency in Quantum Simulations

Quantum computing advance rapidly, offering revolutionary potential in diverse fields, especially in simulating quantum systems. One of the primary challenges in quantum computing is finding ways to improve computational efficiency without sacrificing accuracy.

Krylov subspace methods, originally developed in classical numerical linear algebra, are gaining attention as promising tools to achieve these goals in quantum simulations.

Let’s dive into how Krylov subspace methods work and why they hold immense promise for improving efficiency in quantum simulations.

Understanding Krylov Subspace Methods

The Basics of Krylov Subspace

In classical computing, Krylov subspace methods are techniques used to solve large linear systems of equations and eigenvalue problems. These methods create a sequence of Krylov subspaces that are generated from an initial vector and a matrix, ultimately approximating the solution to complex problems efficiently. For quantum computing, the goal is to adapt these methods to reduce the resource demands of quantum simulations.

The Krylov subspace itself is constructed by a sequence of matrix-vector products, providing a structured way to explore a matrix’s characteristics without needing the entire matrix explicitly. This approach is ideal for handling large, sparse matrices often encountered in quantum simulations.

Key differences between Krylov subspace methods and other quantum simulation techniques.

Metric	Krylov Subspace Methods	Trotterization	Variational Quantum Eigensolver (VQE)	Quantum Phase Estimation (QPE)
Computational Efficiency	High for time-evolution tasks; iterative	Moderate, depends on step size	Lower due to variational optimization	Moderate to High, depending on precision
Resource Requirements	Moderate, scalable with classical resources	Moderate, scales with simulation length	High, requires parameter optimization	High, needs significant qubits and gates
Accuracy	High for short to medium evolution periods	Varies based on step size, accumulates error	High for ground-state estimation	Very High, exact for specific eigenvalues
Circuit Depth	Moderate, requires fewer gates	High, scales with evolution steps	Moderate, adaptive based on ansatz depth	Very High, depends on target precision

Explanation:

Krylov Subspace Methods:
- Computational Efficiency: High for tasks involving time evolution, using an iterative approach.
- Resource Requirements: Moderate, manageable with classical resources.
- Accuracy: High for short- and medium-term simulations.
- Circuit Depth: Moderate, with fewer gate requirements than some alternatives.
Trotterization:
- Computational Efficiency: Moderate; step size affects efficiency.
- Resource Requirements: Moderate, scaling with simulation length.
- Accuracy: Varies with step size and accumulates error over time.
- Circuit Depth: High, proportional to evolution steps.
Variational Quantum Eigensolver (VQE):
- Computational Efficiency: Lower due to variational optimization loops.
- Resource Requirements: High, requiring classical and quantum optimizations.
- Accuracy: High, especially for estimating ground states.
- Circuit Depth: Moderate, adaptable with ansatz depth.
Quantum Phase Estimation (QPE):
- Computational Efficiency: Moderate to high, depending on eigenvalue precision.
- Resource Requirements: High, requiring many qubits and gates.
- Accuracy: Very high for estimating exact eigenvalues.
- Circuit Depth: Very high, scaling with target precision.

Why Use Krylov Subspace in Quantum Simulations?

Quantum simulations frequently involve solving Schrödinger’s equation or related linear algebraic problems that can be computationally expensive. Krylov subspace methods help tackle these challenges by:

Reducing the dimensionality of the problem, allowing faster computations.
Providing approximations that still maintain high accuracy, crucial for simulating complex quantum systems.
Enabling simulations that can run on current quantum hardware with fewer quantum gates and shorter circuit depths.

These advantages make Krylov subspace methods particularly appealing for quantum computing applications that aim to simulate molecular structures, materials, and other complex quantum systems.

How Krylov Subspace Enhances Quantum Efficiency

Reducing Quantum Circuit Depth

One of the significant challenges in quantum computing is the quantum circuit depth, or the number of operations needed to run a quantum algorithm. Quantum circuits with excessive depth can lead to errors and computational instability, especially on today’s noisy quantum computers.

Krylov subspace methods work by creating an approximation in a reduced space, which often leads to shorter quantum circuits. By reducing circuit depth, Krylov methods allow quantum simulations to be more practical on current hardware, paving the way for more realistic, error-resistant computations.

Efficient Handling of Sparse Matrices

Quantum systems often involve sparse matrices, where only a small portion of elements are non-zero. The sparse nature of these matrices poses a challenge, as conventional quantum algorithms might still treat these matrices as dense, wasting resources.

Krylov subspace methods are well-suited for sparse matrices, allowing quantum computers to process only the non-zero elements, thus significantly cutting down computational overhead. This makes Krylov subspace methods especially valuable in fields like quantum chemistry, where Hamiltonians (energy operators) tend to be sparse.

Enhancing Precision in Quantum State Evolution

Another key advantage of Krylov methods is their ability to approximate quantum state evolution accurately. This is critical in quantum dynamics, where evolving a quantum state over time is central to predicting system behavior.

Traditional quantum simulation methods often struggle with maintaining precision over extended time periods, but Krylov subspace methods allow for incremental, accurate approximations. This approach not only preserves the fidelity of quantum state evolution but also enables simulations of larger quantum systems, broadening the scope of what can be studied on existing quantum hardware.

Applications of Krylov Subspace Methods in Quantum Computing

Quantum Chemistry and Material Science

In quantum chemistry, simulating molecular structures requires handling large, complex Hamiltonians, which can be resource-intensive. Krylov subspace methods can significantly reduce the computational demands, making it possible to simulate larger molecules and materials. This capability has practical implications in fields like drug discovery, where researchers use quantum simulations to predict molecular interactions.

Material science also benefits from these methods, as they allow scientists to model quantum properties of new materials with greater efficiency. By leveraging Krylov subspace methods, researchers can explore quantum phase transitions, superconductivity, and other material phenomena more effectively.

Applications and computational impact of Krylov subspace methods in various fields of quantum computing. — Explanation:
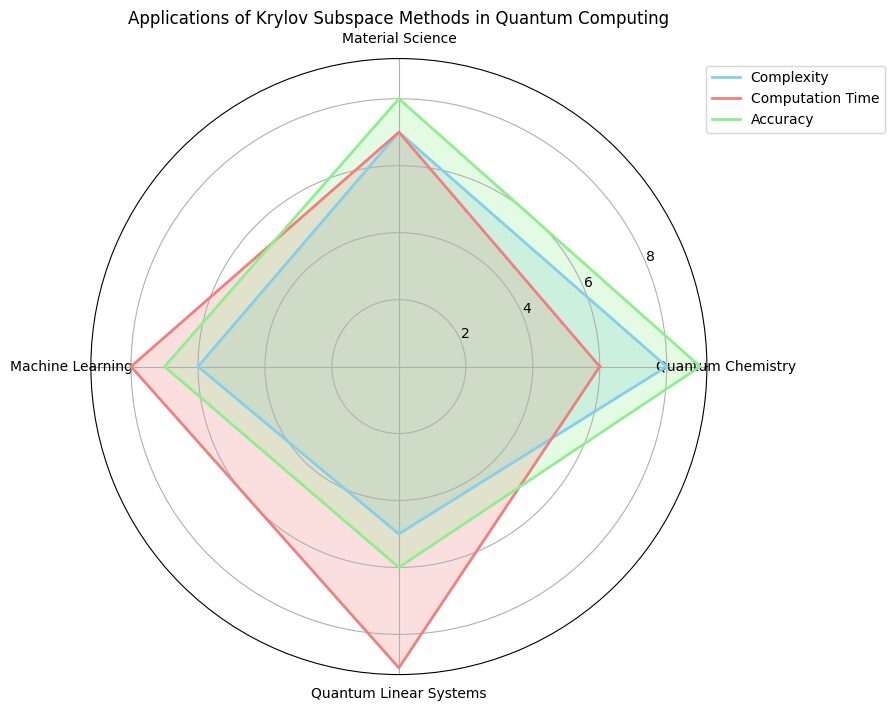
Applications: Each radial axis represents a distinct application area—Quantum Chemistry, Material Science, Machine Learning, and Quantum Linear Systems.
**Metrics**: Complexity, computation time, and accuracy, plotted along each axis to visualize the demands in each field.

Quantum Machine Learning

While Krylov subspace methods are traditionally associated with linear algebra, they are also finding applications in quantum machine learning (QML). By reducing the dimensionality of complex data, Krylov methods can help quantum computers manage larger datasets or train models with greater accuracy. This makes them a valuable tool for developing more efficient QML algorithms, particularly as quantum computers scale up and are used for data-driven applications.

Quantum Algorithms for Linear Systems

Krylov subspace methods also play a role in developing more efficient quantum algorithms for linear systems, such as the quantum linear systems algorithm (QLSA). These algorithms solve large systems of linear equations, a foundational problem in both quantum and classical computing. By integrating Krylov subspace methods, QLSA and similar algorithms can achieve faster, more resource-efficient solutions, bringing quantum advantages to fields as varied as finance, engineering, and beyond.

Challenges and Future Directions for Krylov Subspace Methods in Quantum Computing

Addressing Hardware Limitations

While Krylov subspace methods reduce computational demands, their implementation still requires robust quantum hardware. Today’s quantum computers are prone to noise and decoherence, which can undermine the precision needed for these methods. Future quantum hardware developments are expected to make Krylov subspace methods more practical for a wider range of applications, especially as error-correction techniques improve.

Integrating with Quantum-Classical Hybrid Approaches

Combining Krylov subspace methods with quantum-classical hybrid models could enhance computational efficiency even further. Hybrid approaches allow portions of a quantum problem to be offloaded to classical systems, preserving quantum resources. For instance, the initial matrix-vector products in a Krylov subspace could be handled by a classical processor, while subsequent steps are completed on a quantum computer. This integrated approach could make it feasible to simulate even larger quantum systems.

Challenges in optimizing Krylov subspace methods for efficient quantum computing applications. — **Main Challenge**: Accuracy vs. Resources
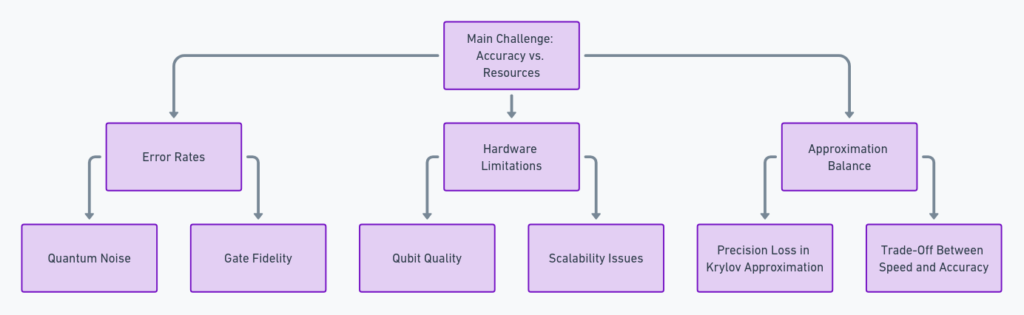
**Error Rates**: Quantum Noise, Gate Fidelity
**Hardware Limitations**: Qubit Quality, Scalability Issues
**Approximation Balance**: Precision Loss in Krylov Approximation, Trade-Off Between Speed and Accuracy

Balancing Accuracy with Resource Requirements

One ongoing challenge is striking the right balance between accuracy and resource demands. Krylov subspace methods offer approximations, and while they can be highly accurate, the precision may vary depending on the problem. Researchers are exploring methods to optimize these approximations, finding ways to reduce computational resources without compromising the quality of the simulation, especially in complex quantum simulations.

Krylov subspace methods are clearly playing an exciting role in quantum computing, offering ways to reduce the computational load while maintaining accuracy. Whether it’s enhancing quantum simulations in chemistry, powering quantum machine learning, or enabling new quantum algorithms for linear systems, these methods are key players in the drive toward more efficient, practical quantum computations.

In the coming years, as quantum technology matures, the combination of Krylov subspace methods and quantum computing promises to unlock new possibilities for research and innovation across various scientific fields.

Conclusion: The Future Impact of Krylov Subspace Methods in Quantum Computing

Krylov subspace methods offer a promising solution to the efficiency challenges in quantum simulations, providing a path toward resource-efficient and accurate quantum computations. By reducing the quantum circuit depth, efficiently handling sparse matrices, and enhancing precision in state evolution, these methods are driving forward the capabilities of current quantum technology.

While there are challenges—such as hardware limitations and the balance between accuracy and resources—ongoing developments in quantum hardware and hybrid approaches are likely to enhance their practicality even further. With applications spanning quantum chemistry, material science, machine learning, and more, Krylov subspace methods hold the potential to transform how we simulate and understand quantum systems.

As researchers continue to explore new techniques and integrate these methods into quantum algorithms, Krylov subspace methods are set to play an essential role in scaling quantum computing for complex real-world applications.

FAQs

What are Krylov subspace methods in simple terms?

Krylov subspace methods are techniques used to solve large systems of equations by creating a sequence of smaller subspaces from an initial matrix and vector. In quantum computing, these methods help reduce the complexity of simulations by working within smaller, manageable subspaces, allowing for efficient approximations without needing the entire problem to be represented.

How do Krylov subspace methods enhance quantum computing efficiency?

By constructing reduced-dimensional spaces, Krylov methods decrease the quantum circuit depth and computational resources required for simulations. They can also handle large, sparse matrices typical in quantum systems more efficiently, making simulations faster and more feasible on current quantum hardware.

Are Krylov subspace methods only used in quantum computing?

No, Krylov subspace methods originated in classical numerical linear algebra and are widely used in scientific computing, engineering, and machine learning. Their application in quantum computing is relatively recent but gaining traction due to the demand for efficient, scalable simulations.

What are the main challenges of using Krylov methods in quantum computing?

The main challenges are tied to hardware limitations in today’s quantum computers, including noise and decoherence that can affect precision. Additionally, Krylov methods produce approximations, which means balancing computational resources with accuracy can be tricky for some quantum problems.

How are Krylov subspace methods applied in quantum simulations?

Krylov methods can be applied in various quantum simulations, such as simulating the time evolution of quantum states and calculating properties in quantum chemistry and materials science. By breaking down these complex tasks into smaller subspaces, quantum computers can more efficiently compute approximate solutions.

Can Krylov subspace methods be used in quantum machine learning?

Yes, Krylov methods are becoming valuable in quantum machine learning (QML), where they help manage larger datasets and train models efficiently. Their ability to reduce dimensionality without sacrificing accuracy makes them useful for developing scalable quantum machine learning algorithms.

What future developments could make Krylov subspace methods more practical?

Advances in quantum hardware, such as improved error correction and reduced noise, will enhance the practicality of Krylov methods in quantum computing. Additionally, hybrid quantum-classical approaches may allow portions of the calculations to be handled by classical computers, making Krylov methods even more resource-efficient.

Why are Krylov subspace methods important for quantum chemistry and material science?

These methods enable more efficient simulations of molecular structures and materials, which require handling large, complex Hamiltonians. By reducing computational demands, Krylov subspace methods allow researchers to simulate larger molecules and materials, aiding in discoveries in fields like drug discovery and material development.

How do Krylov subspace methods affect quantum circuit depth?

Krylov subspace methods reduce quantum circuit depth by creating approximations within smaller subspaces, which require fewer quantum gates. This reduction is crucial because a lower circuit depth allows quantum algorithms to run with fewer errors, making simulations more accurate and feasible on today’s quantum hardware.

Can Krylov subspace methods be combined with other quantum algorithms?

Yes, Krylov subspace methods can be integrated with other quantum algorithms, such as quantum phase estimation or quantum linear system algorithms (QLSA), to enhance performance. By introducing Krylov approximations, these combined methods can handle larger systems or achieve better accuracy while consuming fewer resources.

How do Krylov subspace methods manage accuracy in quantum simulations?

These methods provide approximations, but they maintain high accuracy by incrementally refining solutions through smaller subspaces. By adjusting the subspace size or adding additional terms, Krylov methods allow for a balance between computational efficiency and precision, making them ideal for large-scale simulations where exact solutions are less feasible.

Balancing accuracy with resource requirements in Krylov subspace methods. — **Resource Levels**: Represented across low, medium, and high resource allocations.
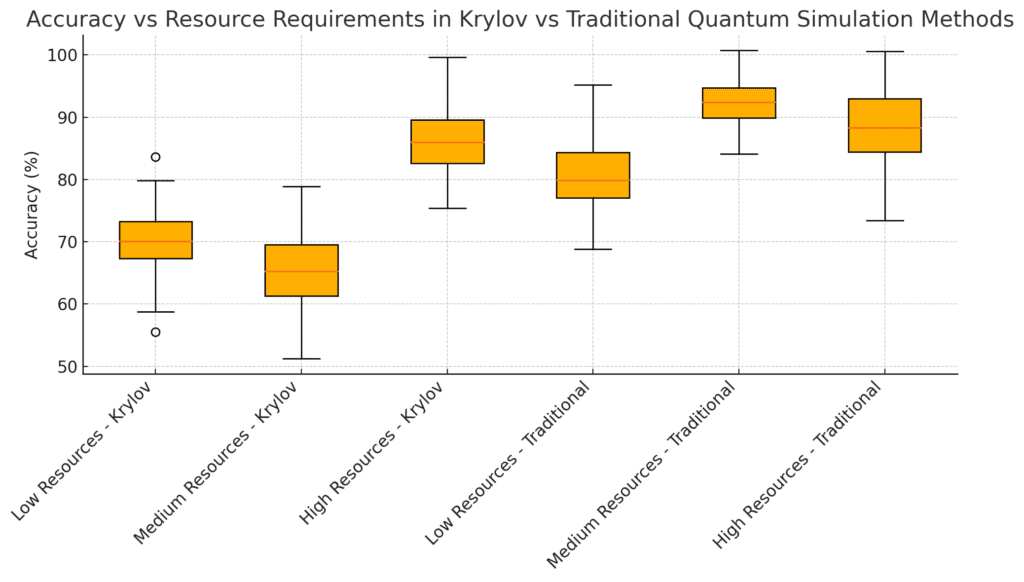
**Accuracy Distribution**: Displays accuracy metrics across different levels, with Krylov methods generally showing higher accuracy at each resource level.

Are Krylov subspace methods suitable for NISQ (Noisy Intermediate-Scale Quantum) devices?

Yes, Krylov subspace methods are particularly valuable on NISQ devices due to their ability to reduce circuit depth and computational load. This makes them suitable for the limited qubit counts and noise levels typical of NISQ devices, enabling meaningful simulations despite hardware constraints.

What are some practical applications of Krylov subspace methods?

Beyond quantum computing, Krylov subspace methods are used in a variety of applications, including signal processing, fluid dynamics, and structural engineering. In these fields, they allow for efficient computations in systems with many variables, such as fluid flow in simulations or stress analysis in engineering.

Do Krylov subspace methods require specialized quantum hardware?

While Krylov methods don’t require unique hardware, they do benefit from hardware with lower error rates and longer coherence times to maintain accuracy. As quantum hardware improves, Krylov subspace methods are expected to become even more effective and widely applicable, particularly in high-precision simulations.

How do Krylov subspace methods differ from other linear algebra approaches?

Unlike methods that operate on the entire matrix, Krylov subspace methods focus on building a sequence of subspaces from initial vectors, which reduces computational requirements. This makes them more efficient than methods that require all matrix elements to be considered simultaneously, particularly useful in large, sparse systems common in quantum simulations.

What role do Krylov subspace methods play in quantum error mitigation?

Krylov subspace methods indirectly contribute to quantum error mitigation by reducing the number of operations needed in a quantum circuit. This shorter circuit depth decreases the exposure to noise and potential errors, enhancing the overall fidelity of quantum simulations without requiring complex error-correction protocols.

Can Krylov subspace methods be applied to time-dependent quantum simulations?

Yes, Krylov methods are well-suited for time-dependent quantum simulations due to their iterative approach. By advancing quantum states over small time increments, these methods allow for precise control over state evolution, making them highly effective for simulations that require time-based calculations, such as chemical reactions or particle interactions.