
Comparing Optimization Techniques
Optimization techniques are critical in fields like engineering, machine learning, and economics, where finding the best solution to complex problems is crucial. Particle Swarm Optimization (PSO), Genetic Algorithms (GA), and Simulated Annealing (SA) are among the most popular methods.
Each offers unique advantages and is suited to different types of problems. In this article, we’ll dive into the differences, strengths, and weaknesses of these techniques and explore when to use each one.
Understanding Particle Swarm Optimization (PSO)
How Does Particle Swarm Optimization Work?
Particle Swarm Optimization is inspired by the collective behavior of birds flocking or fish schooling. In PSO, a group of potential solutions, known as particles, “fly” through the solution space in search of the optimal point. Each particle adjusts its position based on its own experience and the experiences of its neighbors.
In PSO:
- Particles are initialized randomly.
- They “learn” from each other’s successes.
- They adjust their positions toward the best-known solutions.
This technique is particularly effective in continuous, multi-dimensional spaces, where the optimal solution can change based on dynamic conditions.
Advantages of PSO
PSO is known for its simplicity and speed. Since particles don’t require complex operators like mutation or crossover, as in genetic algorithms, they often converge quickly. PSO is also highly adaptable to non-linear, multi-objective, and noisy problems, making it ideal for tasks like neural network training and signal processing.
Disadvantages of PSO
A potential drawback of PSO is its tendency to get stuck in local optima—especially in complex, rugged landscapes. PSO particles may converge prematurely if there isn’t enough diversity in the swarm, which can limit its effectiveness in highly variable solution spaces.
Genetic Algorithms (GA): Evolution-Based Optimization
How Do Genetic Algorithms Work?
Genetic Algorithms take inspiration from biological evolution, using concepts like mutation, crossover, and selection to evolve a population of solutions over generations. Each solution, or individual, is represented by a chromosome, and over time, these chromosomes evolve to better fit the problem at hand.
In GAs:
- Solutions are combined and mutated to explore new options.
- Fitness functions evaluate how “fit” or optimal each solution is.
- The population evolves through generations, guided by selection and genetic diversity.
This makes GAs effective for a range of problems, including combinatorial tasks like scheduling and route optimization.
Advantages of GAs
GAs excel in exploring large search spaces and are robust against complex, non-linear problems. They don’t require gradient information, so they’re great for problems with discontinuous functions or when there are many local optima. GAs can also maintain diversity longer, helping avoid the trap of local optima.
Disadvantages of GAs
The main drawback of GAs is their relatively high computational cost. Since they rely on many evaluations per generation, they can be slower than other methods, particularly for problems with high-dimensional solution spaces. GAs also require careful tuning of parameters like mutation rate, crossover probability, and population size to perform effectively.
Simulated Annealing (SA): A Temperature-Based Technique
How Does Simulated Annealing Work?
Simulated Annealing is based on the annealing process in metallurgy, where a material is heated and then slowly cooled to achieve a stable structure. In optimization, this technique “heats” the solution space, allowing solutions to explore widely before “cooling” and settling into an optimal state.
In SA:
- Solutions randomly move through the search space.
- A temperature parameter controls the probability of accepting worse solutions, helping avoid local minima.
- As temperature decreases, the algorithm becomes more selective, focusing on refining the current best solution.
This temperature-controlled process allows SA to balance exploration and exploitation, making it suitable for discrete optimization tasks like job scheduling and timetabling.
Advantages of SA
SA is simple to implement and requires fewer parameters than GAs or PSO. It’s particularly effective at escaping local optima, thanks to its probabilistic acceptance of worse solutions at higher “temperatures.” This feature makes it a good fit for optimization landscapes with many local minima.
Disadvantages of SA
Simulated Annealing may struggle in high-dimensional, continuous spaces, where PSO or GAs often perform better. Additionally, while it can escape local optima, SA’s convergence rate can be slow, especially if the cooling schedule is not carefully designed.
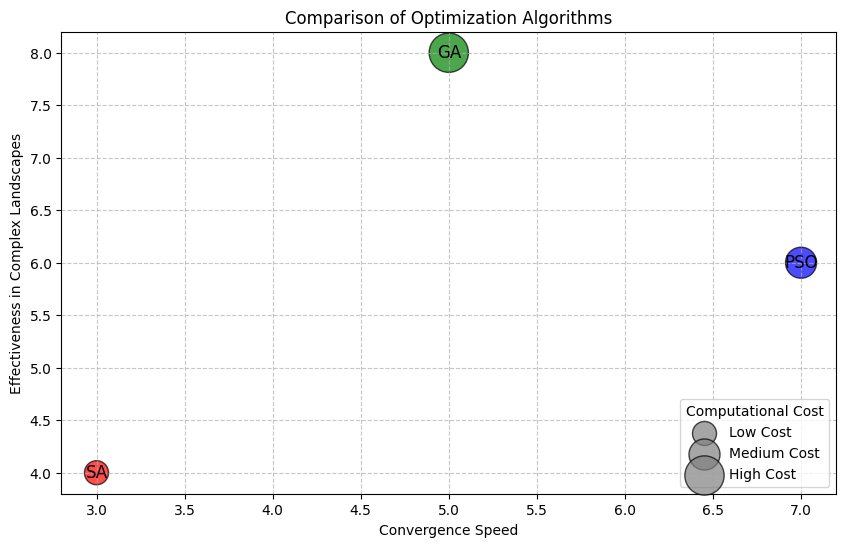
Comparing Performance: PSO vs. GA vs. SA
Convergence Speed and Computational Cost
- PSO generally converges faster because particles learn from one another directly, but it risks premature convergence.
- GAs tend to be slower due to the high number of evaluations, though they handle complex search spaces well.
- SA is often slower due to its cooling schedule, which is necessary to avoid suboptimal solutions.
Suitability for Different Problem Types
- PSO is ideal for continuous, multi-objective, and real-valued problems.
- GAs excel in discrete, combinatorial tasks and are versatile across varied problem types.
- SA is effective for problems where the solution space has many local optima and can work well with discrete data.
Avoidance of Local Optima
- PSO has moderate resistance to local optima due to particle diversity but may struggle in complex landscapes.
- GAs maintain diversity well, helping them escape local traps more reliably.
- SA is highly resistant to local optima due to its probabilistic acceptance of worse solutions at higher temperatures.
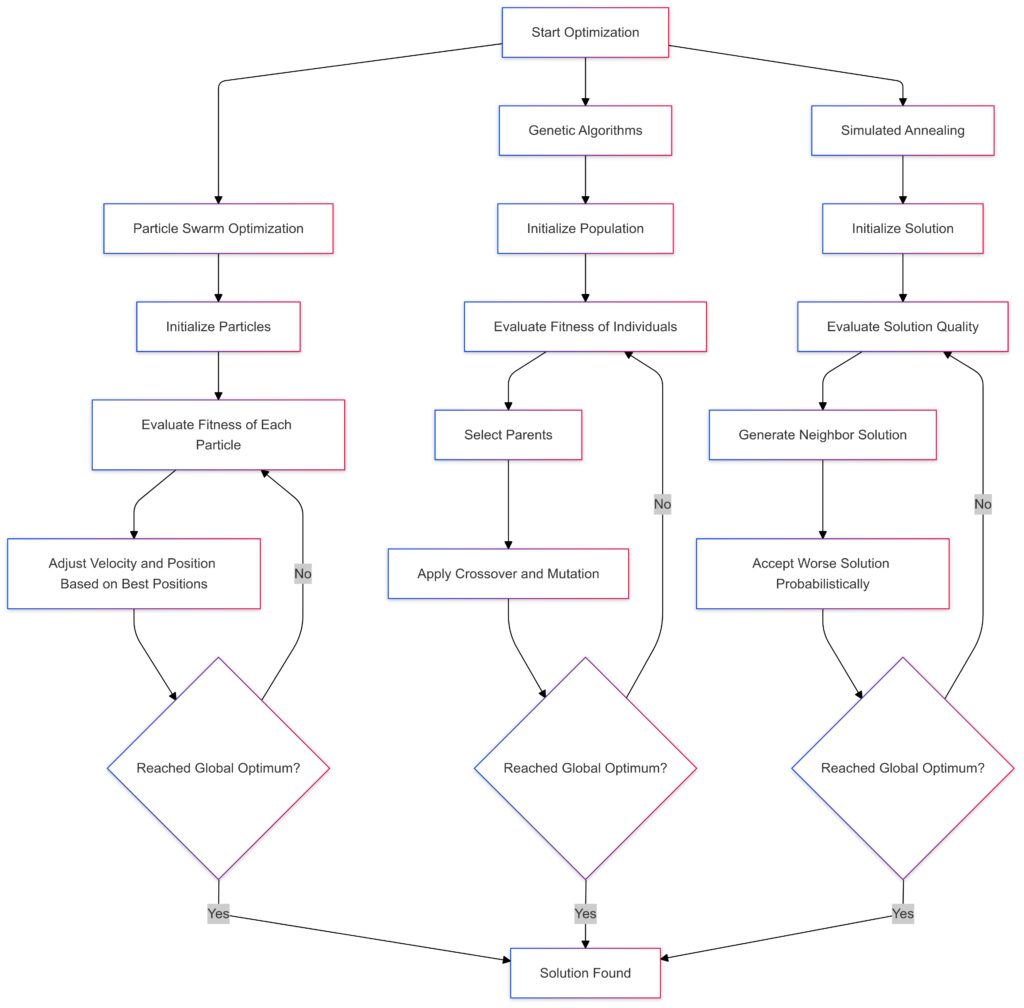
PSO: Adjusts particle velocity and position based on the best-known positions to move toward the global optimum.
GA: Uses crossover and mutation after selecting parents to generate new solutions.
SA: Accepts worse solutions probabilistically to escape local optima, gradually reducing the likelihood over time.
Each algorithm iteratively tests solutions, using distinct methods to avoid getting stuck in suboptimal regions.
Choosing the Right Technique
When to Use Particle Swarm Optimization
Use PSO when:
- The problem is continuous and multi-dimensional.
- Computational resources are limited.
- You’re working with dynamic or multi-objective optimization tasks.
Example Applications:
- Parameter tuning for neural networks.
- Optimizing control systems in robotics.
When to Use Genetic Algorithms
Use GA when:
- The problem involves combinatorial optimization or discrete variables.
- You need a technique robust against rugged landscapes.
- Diversity and adaptability are priorities.
Example Applications:
- Route optimization for logistics.
- Complex scheduling problems.
When to Use Simulated Annealing
Use SA when:
- You’re dealing with a landscape filled with local optima.
- A probabilistic approach fits well with the problem.
- Simplicity is desired, and computational time is flexible.
Example Applications:
- Resource allocation in operations research.
- Network design problems.
In the next section, we’ll look at practical case studies and performance benchmarks, showing how these methods perform in real-world scenarios. This will provide deeper insight into selecting the best optimization approach for your needs.
Real-World Case Studies: Comparing PSO, GA, and SA in Action
To truly understand the strengths and weaknesses of these optimization methods, it helps to look at how they perform in real-world scenarios. Below, we’ll explore case studies that illustrate the applications of Particle Swarm Optimization, Genetic Algorithms, and Simulated Annealing in various industries.
Case Study 1: Manufacturing – Job Scheduling and Resource Allocation
PSO in Manufacturing
In manufacturing, efficient job scheduling and resource allocation are essential. Here, Particle Swarm Optimization can be useful, particularly when the problem involves multiple objectives, such as minimizing production time and cost simultaneously.
Results with PSO:
- Pros: PSO’s rapid convergence makes it a good fit for time-sensitive scheduling problems. It’s also easy to adapt for multi-objective optimization.
- Cons: In complex scenarios with highly variable constraints, PSO might converge too early on a suboptimal schedule, potentially requiring adjustments to avoid this.
GA in Manufacturing
Genetic Algorithms offer an edge in job scheduling because of their robust search and adaptability, especially in discrete problems where machines, time slots, and tasks need optimal alignment.
Results with GA:
- Pros: GAs can explore diverse scheduling combinations, making them more likely to find high-quality solutions in complex, constraint-heavy environments.
- Cons: GAs require longer run times, so they might be less suitable if schedules need frequent updates.
SA in Manufacturing
In highly constrained scheduling problems, Simulated Annealing can work effectively, especially when a near-optimal solution is acceptable.
Results with SA:
- Pros: SA’s ability to escape local optima is advantageous when schedules need adjustment in constrained settings, like job shop scheduling.
- Cons: The slower convergence of SA can delay scheduling, so it’s better suited for scenarios with flexible timing.
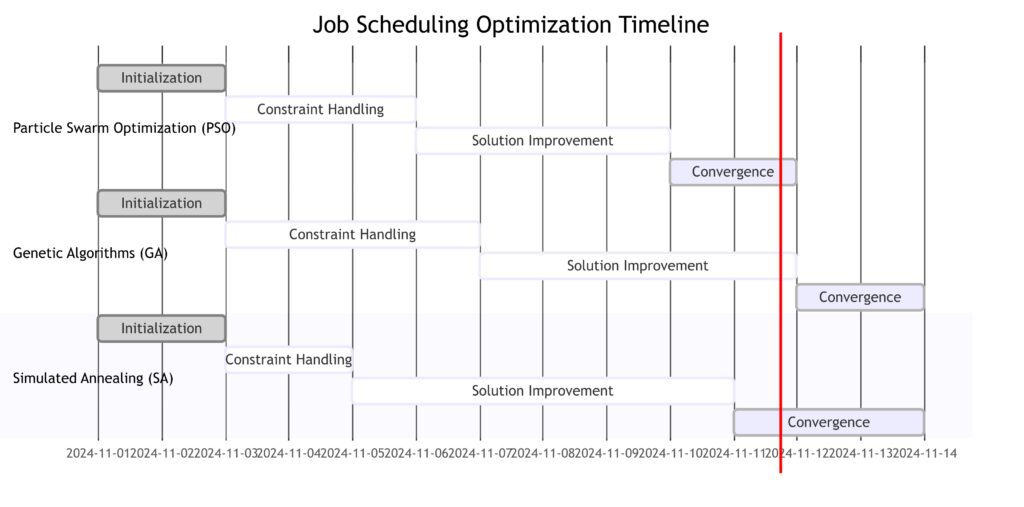
Initialization starts for all methods on the same day.
Constraint Handling and Solution Improvement stages show the unique durations each method takes.
Convergence marks the completion, with SA reaching it slightly sooner than GA, and PSO achieving convergence first.
Each method has its own color-coded timeline, showing their individual progression toward optimization.
Case Study 2: Transportation and Logistics – Route Optimization
PSO in Logistics
For complex route optimization, Particle Swarm Optimization is useful in finding short, fuel-efficient paths, especially when there are numerous potential routes.
Results with PSO:
- Pros: Fast convergence and real-time adaptability make PSO effective for large-scale logistics problems, where routes need rapid updating.
- Cons: PSO may get stuck in suboptimal routes if the solution space is too rugged, which can affect its performance in highly irregular networks.
GA in Logistics
When a logistics problem involves numerous locations and constraints, Genetic Algorithms excel due to their strong exploratory ability and suitability for discrete optimization.
Results with GA:
- Pros: GAs are highly effective in scenarios requiring complex optimization, like vehicle routing with multiple delivery points and time windows.
- Cons: Longer computation times can be a drawback, particularly in real-time route optimization, where speed is critical.
SA in Logistics
Simulated Annealing is beneficial in route optimization problems, particularly where the solution involves minimizing travel time while accommodating a high number of stops.
Results with SA:
- Pros: SA can find efficient routes by accepting slight increases in travel time to explore different paths, making it effective in urban or congested networks.
- Cons: While effective, SA’s slower convergence makes it less practical for highly time-sensitive logistics needs.
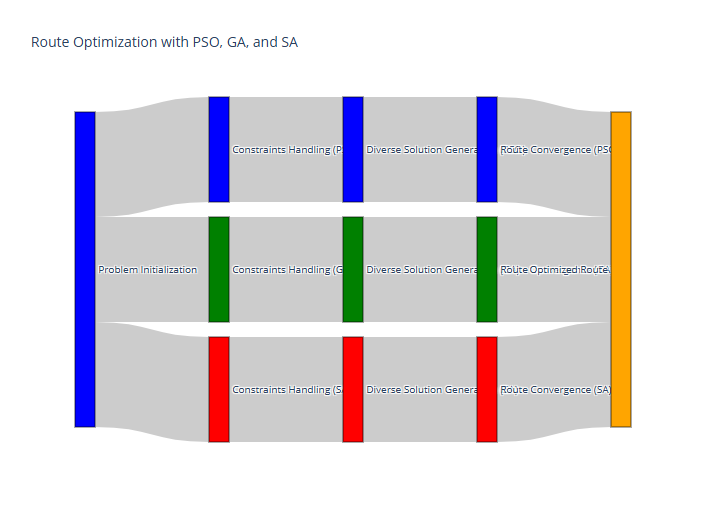
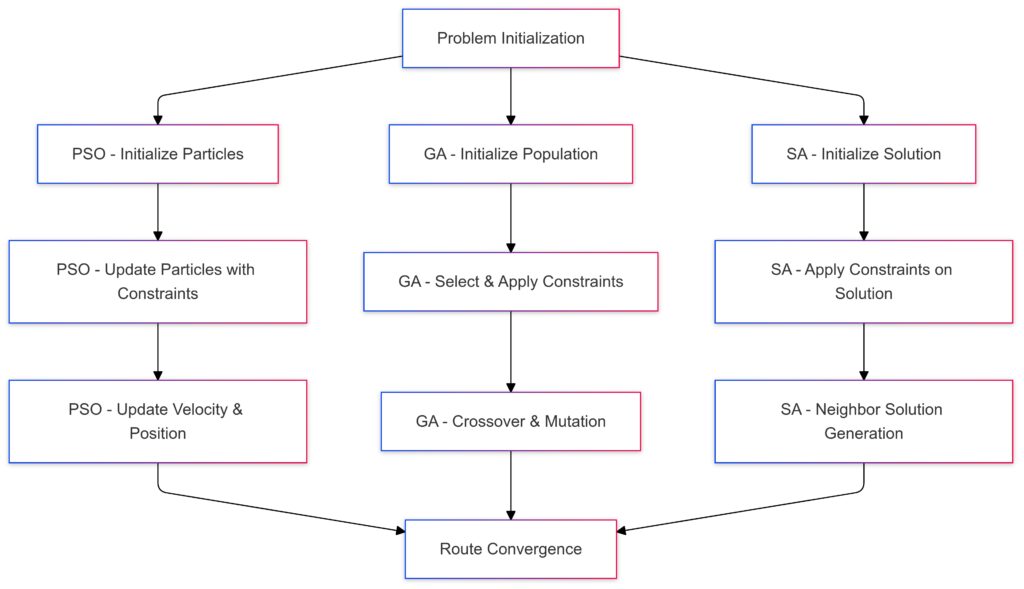
Problem Initialization begins each algorithm.
Constraints Handling is customized per algorithm:PSO adjusts particles with constraints.
GA applies selection and crossover.
SA considers neighboring solutions.
Each method progresses through solution updates, converging on an optimized route.
This visualization highlights the distinct pathways each algorithm follows to achieve convergence in a logistics route optimization context.
Case Study 3: Finance – Portfolio Optimization
PSO in Finance
In finance, portfolio optimization involves selecting an optimal set of assets that maximizes returns and minimizes risk. PSO can handle these multi-objective optimization tasks well, adjusting asset allocations based on various risk-return profiles.
Results with PSO:
- Pros: PSO’s ability to balance multiple objectives makes it a natural fit for financial modeling, especially for risk and return.
- Cons: PSO might struggle if the asset space is highly volatile or complex, where other methods may perform better.
GA in Finance
Genetic Algorithms have been widely applied in portfolio optimization, as they can explore a wide range of asset combinations and diversification strategies.
Results with GA:
- Pros: GAs can handle diverse financial goals (e.g., return maximization, risk minimization) while accommodating different asset constraints, like sector diversification.
- Cons: High computational requirements may be a drawback, especially in markets with a high volume of assets.
SA in Finance
For simpler portfolio problems or when a near-optimal solution suffices, Simulated Annealing can efficiently optimize a portfolio’s risk-return ratio.
Results with SA:
- Pros: SA’s probabilistic approach is advantageous in volatile markets, as it allows exploration of non-optimal solutions for better risk management.
- Cons: Slower convergence limits SA’s application in real-time, high-frequency trading or portfolios requiring rapid rebalancing.
Practical Performance Benchmarks: Testing Efficiency and Convergence
Test Scenario 1: Solving the Traveling Salesman Problem (TSP)
The Traveling Salesman Problem (TSP) is a classic test for optimization algorithms, as it requires finding the shortest possible route visiting multiple cities once.
- PSO tends to perform well in TSP due to its speed but may struggle in highly complex configurations.
- GA excels in larger TSP instances, as its crossover and mutation operations effectively explore diverse paths.
- SA finds good solutions in TSP by avoiding premature convergence, though slower to compute.
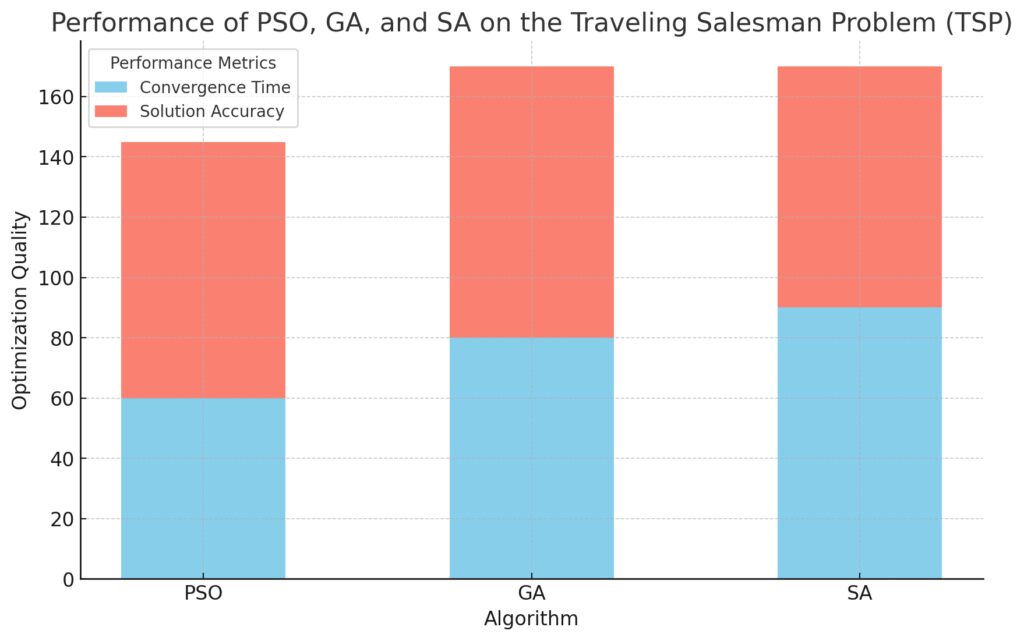
Convergence Time is shown in blue, indicating the speed at which each algorithm reaches a solution.
Solution Accuracy is shown in red, representing how close the solution is to the optimal route.
Test Scenario 2: Optimization in Machine Learning Model Training
Machine learning model training often involves fine-tuning parameters to maximize performance.
- PSO is effective due to its fast convergence and adaptability to continuous parameter spaces, such as neural network training.
- GA also performs well, exploring a broad set of hyperparameters, though requiring more computation.
- SA can optimize hyperparameters but may be too slow for extensive ML training.
Test Scenario 3: Continuous vs. Discrete Optimization Challenges
Optimization challenges often differ between continuous (e.g., adjusting weights) and discrete (e.g., selecting a subset) problem spaces.
- PSO excels in continuous spaces with its smooth convergence but struggles in purely discrete scenarios.
- GA adapts well to both continuous and discrete problems, especially where diversity is needed.
- SA is better suited for discrete challenges with local optima, though slower than PSO in continuous tasks.
Final Considerations: Key Takeaways for Optimal Technique Selection
Selecting the right optimization technique depends on the problem’s nature, computational resources, and the desired solution quality. Here’s a quick recap of which methods fit which scenarios best:
- PSO is the go-to for continuous, multi-dimensional problems where fast convergence is critical.
- GA is ideal for complex, constraint-heavy problems, especially when maintaining diversity is key.
- SA shines in scenarios with local optima or discrete solution spaces where convergence speed is less crucial.
In the end, many industries and applications may benefit from combining techniques or adjusting parameters to get the best results. Hybrid approaches, such as integrating PSO with GA, have shown promising results in balancing exploration and convergence, especially in complex and high-dimensional landscapes.
Conclusion: Choosing the Right Optimization Method for Your Needs
When comparing Particle Swarm Optimization (PSO), Genetic Algorithms (GA), and Simulated Annealing (SA), each technique stands out for its unique strengths. The choice of algorithm depends heavily on the type of problem, solution requirements, and available computational resources.
Key Takeaways for Decision-Making
- For Fast Convergence in Continuous Spaces:
Particle Swarm Optimization is an excellent choice if you need fast results and are working within continuous, multi-objective landscapes. Its simplicity and quick convergence make it suitable for real-time control systems and neural network training, where time is critical. - For Robust Exploration in Discrete or Complex Landscapes:
Genetic Algorithms excel in complex, constraint-laden environments, where diverse exploration can avoid local optima. They’re especially effective in combinatorial tasks like scheduling and route optimization where high-quality solutions are more valuable than speed. - For Local Optima Avoidance in Highly Constrained Problems:
Simulated Annealing provides a powerful way to escape local optima, making it ideal for problems with rough solution landscapes, like timetabling or resource allocation. Its probabilistic approach allows exploration of varied solutions, though it may require more time to converge.
When to Consider Hybrid Approaches
In practice, combining these techniques can enhance performance across complex tasks. Hybrid algorithms such as PSO-GA or GA-SA combine the fast convergence of one method with the robustness or exploration depth of another, balancing exploration and exploitation. For example:
- PSO-GA Hybrids: Can combine GA’s exploration of complex landscapes with PSO’s quick convergence, useful in large-scale engineering problems.
- GA-SA Hybrids: Use GA to diversify solutions while SA refines the final selection, making it ideal for highly constrained optimization, such as financial portfolio management.
Final Thoughts
Whether you’re tuning machine learning parameters, optimizing supply chains, or managing financial portfolios, selecting the right optimization approach can significantly impact your solution quality and efficiency. Experimenting with these algorithms, or even hybridizing them, can help find the best balance for specific problems, paving the way for innovation and efficiency in complex decision-making.
By understanding each method’s strengths and adapting them to your needs, you can better navigate the world of optimization and make confident choices that improve outcomes and reduce costs.
FAQs
How does Particle Swarm Optimization differ from Genetic Algorithms?
Particle Swarm Optimization (PSO) is based on social behavior models, where particles adjust based on personal and neighborhood experiences to reach an optimal solution. In contrast, Genetic Algorithms (GA) use principles of biological evolution, like selection, crossover, and mutation to evolve solutions across generations. While PSO relies on collaboration within a group, GA relies on individual “survival” through generations.
Is Simulated Annealing suitable for all types of optimization problems?
Simulated Annealing (SA) is particularly effective for discrete and constrained problems where local optima are common, such as job scheduling and combinatorial tasks. However, it may not be as efficient for continuous, multi-dimensional problems like those found in machine learning parameter tuning, where PSO or GA often perform better.
Which algorithm is best for multi-objective optimization?
Both PSO and GA are strong candidates for multi-objective optimization. PSO handles multiple objectives well due to particles’ ability to adapt based on the best positions. GA, with its genetic diversity and crossover operations, is effective in exploring varied solutions for multi-objective tasks. For complex, non-linear problems, GA may offer an edge due to its robust exploration.
Why might one choose a hybrid optimization approach?
Hybrid approaches, such as PSO-GA or GA-SA, combine strengths from multiple algorithms. For instance, PSO-GA hybrids benefit from GA’s deep exploration and PSO’s fast convergence, making them effective in engineering or logistics. Hybrid methods are useful when a balance between diverse exploration and efficient convergence is necessary, especially for high-dimensional or rugged landscapes.
Are Genetic Algorithms suitable for real-time optimization?
Genetic Algorithms are not typically ideal for real-time optimization due to their higher computational requirements and slower convergence. However, they are effective in applications where finding a high-quality solution is more critical than speed, such as in financial portfolio optimization or complex scheduling. For real-time applications, PSO’s faster convergence may be a better option.
Can these algorithms be used for machine learning model training?
Yes, all three algorithms—PSO, GA, and SA—can be applied in machine learning model training for tuning hyperparameters. PSO is often preferred for continuous hyperparameter spaces due to its speed and adaptability. GA can be used for both discrete and continuous hyperparameters, though it requires more computation. SA is less common in machine learning due to its slower convergence but may work in small-scale tuning tasks.
What are the main limitations of each optimization method?
- PSO: Risk of premature convergence in complex landscapes due to lack of diversity.
- GA: High computational cost due to numerous evaluations and parameter tuning needs.
- SA: Slower convergence, making it unsuitable for large-scale or time-sensitive tasks.
How important is parameter tuning for these algorithms?
Parameter tuning is essential for achieving optimal performance in Genetic Algorithms and Simulated Annealing. GAs require careful adjustment of mutation rate, crossover probability, and population size, while SA depends on a well-designed cooling schedule. PSO is generally easier to tune, though adjusting inertia weights and cognitive/social coefficients can improve results in complex scenarios.
Can these optimization algorithms handle constraints?
Yes, all three algorithms can handle constraints, but they approach them differently:
- PSO can incorporate constraints by penalizing particles that violate constraints or using boundary conditions to guide particles within limits.
- GA handles constraints well through penalty functions and feasibility operators, which discard infeasible solutions during selection, crossover, or mutation.
- SA can include constraints by using a penalty function or by modifying the acceptance criteria to avoid infeasible solutions.
Each method can be adapted for constraint-heavy problems, though GAs are often preferred in highly complex, multi-constraint environments.
Which algorithm is best for avoiding local optima?
Simulated Annealing is often the best for avoiding local optima, thanks to its probabilistic acceptance of non-optimal solutions during the “annealing” process. This helps it escape from local optima, especially in rugged search spaces. GAs also perform well with local optima due to their diverse population, while PSO can sometimes struggle unless diversity is introduced in the swarm.
Are these algorithms suitable for large-scale problems?
Each algorithm can handle large-scale problems, but computational efficiency varies:
- PSO is computationally efficient and performs well on large, continuous problems.
- GA can scale with large problems, though high dimensionality can make it slower due to the need for a large population and numerous generations.
- SA is less suited to large-scale problems as its convergence can be slow, especially if the solution space is vast.
For extremely large or high-dimensional problems, hybrid methods or parallel computing techniques may improve efficiency.
How does convergence differ among PSO, GA, and SA?
- PSO usually converges quickly as particles adapt based on individual and group experience, but it may stop prematurely in some cases.
- GA convergence depends on population diversity; GAs explore widely but may require more generations to stabilize, making them slower but thorough.
- SA has controlled convergence with its cooling schedule, but it’s often slower as it seeks to avoid local optima. Convergence can be improved with an adaptive cooling rate.
Choosing an algorithm with the right convergence characteristics is crucial when deadlines or computational limits are tight.
How does the choice of initial parameters affect each algorithm?
Initial parameters significantly impact performance for all three:
- PSO relies on parameters like inertia weight and cognitive/social coefficients, which can impact speed and accuracy.
- GA needs optimal mutation rate, crossover probability, and population size, which influence solution diversity and convergence rate.
- SA depends heavily on an effective cooling schedule; an improper schedule may lead to premature convergence or excessive run times.
Fine-tuning these parameters can improve results, though it may require trial and error or optimization techniques.
Are these algorithms suitable for dynamic optimization problems?
Dynamic optimization problems, where the optimal solution changes over time, are challenging but manageable:
- PSO adapts well as particles are influenced by the ongoing best-known positions, making it suitable for real-time adaptation.
- GA can adjust dynamically but may require more time to evolve the population to fit the new conditions, potentially reducing responsiveness.
- SA is less suited to dynamic problems due to its structured cooling schedule, which doesn’t adapt well to changing objectives.
PSO is generally best for dynamic environments, while GA can work well if adjustments are made to maintain population diversity in changing conditions.
Can these algorithms be parallelized for faster performance?
Yes, all three algorithms can be parallelized, making them more efficient for large or computationally intense problems:
- PSO can parallelize each particle’s evaluation, significantly reducing runtime in large search spaces.
- GA allows parallel evaluation of individuals in the population, with separate processors handling mutation or crossover processes.
- SA can run multiple independent annealing processes in parallel, though this is less common.
Parallel processing improves scalability, making these algorithms more suitable for high-dimensional problems or scenarios requiring rapid updates.
How does each algorithm handle noisy or uncertain environments?
In environments where the objective function may be noisy or uncertain (e.g., real-world applications with fluctuating data), each algorithm performs differently:
- PSO is relatively resilient to noise because particles adjust based on individual and group success, which helps average out random fluctuations. However, it may converge prematurely in highly noisy conditions.
- GA handles noise well by maintaining population diversity and exploring broad solution areas. This diversity makes GAs less sensitive to fluctuations and better suited for uncertain environments, though they require more evaluations.
- SA can work in noisy environments by accepting suboptimal solutions probabilistically, which helps the algorithm avoid noise-related traps. However, SA’s performance in noisy conditions heavily depends on the cooling schedule, and it can be slower than PSO or GA.
For applications with high uncertainty, GAs often perform best due to their robust exploration, while PSO can also be effective with modifications to increase diversity.
Are these algorithms appropriate for multi-objective optimization?
All three algorithms can handle multi-objective optimization, though they vary in approach:
- PSO has dedicated versions, like Multi-Objective PSO (MOPSO), which track non-dominated solutions and store them in an archive. MOPSO is popular in multi-objective optimization because it can balance competing objectives efficiently.
- GA is highly adaptable for multi-objective problems with techniques like Non-dominated Sorting GA (NSGA-II), which rank solutions based on their performance across objectives. GA-based methods are often used in multi-objective optimization because they maintain diversity and search across objectives effectively.
- SA can handle multi-objective problems but is less common for this purpose, as balancing multiple objectives while cooling is challenging. Some variants exist, though SA’s single-solution approach makes it less suited to complex multi-objective tasks.
Multi-objective GAs are generally preferred for problems requiring a diverse set of trade-off solutions, while MOPSO is useful when faster convergence is needed.
How do these algorithms perform in problems with constrained search spaces?
Constrained problems, where solutions must meet strict criteria, often benefit from certain adaptation techniques:
- PSO can be adapted for constraints by using penalty functions or enforcing bounds, though particles may still struggle with tight constraints if they limit exploration. Penalty functions that increase with constraint violations help guide particles back into feasible regions.
- GA naturally handles constraints well, with genetic operators that maintain feasible solutions, often by integrating repair functions or applying feasibility checks during crossover and mutation.
- SA can also use penalty functions and adjusts its acceptance criteria to reject solutions that don’t meet constraints. It’s generally effective in constrained problems but may be slower if constraints limit exploration significantly.
In constraint-heavy problems, GA tends to perform best, especially if constraints are complex, as it can discard infeasible solutions through selection and evolve feasible ones over generations.
Are hybrid algorithms often more effective than standalone PSO, GA, or SA?
Yes, hybrid algorithms can provide a balance between exploration and exploitation, often outperforming standalone methods:
- PSO-GA hybrids combine PSO’s fast convergence with GA’s strong diversity, making them ideal for complex optimization tasks like feature selection and multi-objective tasks.
- GA-SA hybrids use GA’s exploration to generate diverse solutions, followed by SA’s focused search for fine-tuning, which can be effective in problems like resource allocation or network design.
- PSO-SA hybrids leverage PSO’s convergence speed and SA’s ability to escape local optima, providing a balance that works well in high-dimensional, rugged landscapes.
These hybrid approaches require additional tuning but are highly effective in situations where a single algorithm struggles to balance exploration and convergence.
Do these algorithms require different levels of computational power?
The computational requirements vary based on the algorithm and the problem’s complexity:
- PSO is computationally light, as it doesn’t require complex operators, making it suitable for high-dimensional problems or real-time applications with limited resources.
- GA typically requires more computational power due to its use of selection, crossover, and mutation, especially with large populations or complex fitness evaluations. It’s more suitable for applications with higher computational resources or batch processing.
- SA is computationally light per iteration but can be slow due to its sequential nature, especially with a gradual cooling schedule. It’s often best for smaller problems or where computation time isn’t a strict limitation.
For high-dimensional or real-time applications, PSO or hybrid methods may be preferable, while GA can be more computationally intensive.
Which algorithm is the best choice for machine learning hyperparameter tuning?
Each algorithm can be used for hyperparameter tuning in machine learning, with different strengths:
- PSO is popular for continuous hyperparameter tuning due to its fast convergence and simplicity, making it effective for tuning neural network parameters or support vector machines.
- GA is excellent for hyperparameter tuning in both continuous and discrete spaces, as it can explore diverse configurations effectively, though it may require more time.
- SA can tune hyperparameters, but it’s generally slower and less common for large-scale machine learning models.
PSO is typically the best choice for real-time model tuning, while GA may be more appropriate for complex configurations requiring thorough exploration.
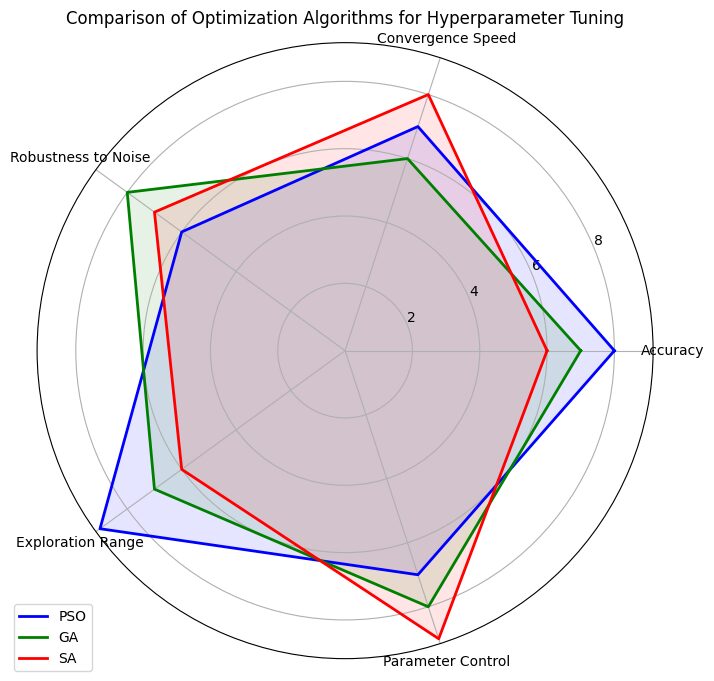
Accuracy: PSO and GA perform well, with GA showing moderate performance.
Convergence Speed: PSO leads, followed by GA, with SA slower overall.
Robustness to Noise: SA is the most robust to noise, while PSO and GA are moderate.
Exploration Range: GA excels in exploration, beneficial for finding diverse solutions.
Parameter Control: PSO offers strong parameter control, supporting fine-tuning.
How adaptable are these algorithms to different problem types?
Each algorithm can be adapted to various types of optimization problems with specific modifications:
- PSO can be modified with variants like Discrete PSO for non-continuous problems or Multi-objective PSO (MOPSO) for multi-objective tasks. It’s adaptable but best suited for continuous spaces.
- GA is highly flexible with different crossover, mutation, and selection techniques, making it ideal for a wide range of problems, from discrete to multi-objective and constrained tasks.
- SA can be adapted with cooling schedules or hybridized, though it’s less common for continuous or multi-objective problems due to its single-solution nature.
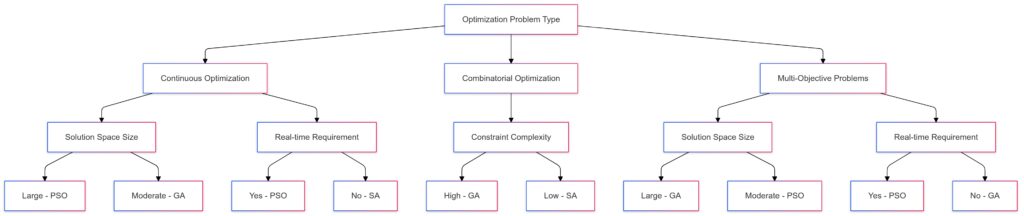
Continuous Optimization: Factors include Solution Space Size and Real-time Requirement.
Combinatorial Optimization: Focuses on Constraint Complexity.
Multi-Objective Problems: Considers Solution Space Size and Real-time Requirement.
Each branch leads to an optimal algorithm choice depending on the problem’s specific requirements.
In terms of versatility, GA is the most adaptable, followed by PSO with modifications for non-standard problems.
Resources
Research Papers and Articles
- “A Particle Swarm Optimization Tutorial” by James Kennedy and Russell C. Eberhart
This foundational paper by the inventors of PSO provides a tutorial-style introduction to PSO, including mathematical formulations, basic concepts, and potential applications.
Link to paper - “Genetic Algorithms in Search, Optimization, and Machine Learning” by David E. Goldberg
This classic paper covers the basics of GAs and presents foundational knowledge on the theory and implementation of genetic algorithms. It’s widely cited and used as a reference for GA research.
Link to paper - “Simulated Annealing: Theory and Applications” by P.J. van Laarhoven and E.H.L. Aarts
A comprehensive paper that explains the theoretical underpinnings of SA, as well as its applications in combinatorial optimization. It’s an excellent resource for understanding the core mechanics of SA.
Link to paper - “A Survey of Metaheuristic Techniques for Optimization” by Siddhartha Bhattacharyya et al.
This survey paper reviews a variety of metaheuristic techniques, including PSO, GA, and SA, and provides comparative insights, making it helpful for researchers or practitioners choosing an appropriate algorithm.
Link to paper
Websites and Open-Source Libraries
- GitHub – Open Source Implementations
- DEAP (Distributed Evolutionary Algorithms in Python): A popular library for implementing GAs and other evolutionary algorithms. It’s well-documented and ideal for those looking to experiment with GA.
GitHub DEAP - PySwarms: A Python library dedicated to PSO, offering easy-to-use implementations with a range of options for custom tuning.
GitHub PySwarms - Simulated Annealing in SciPy: SciPy offers a built-in SA implementation within its
optimizemodule, suitable for basic optimization tasks.
SciPy Simulated Annealing
- DEAP (Distributed Evolutionary Algorithms in Python): A popular library for implementing GAs and other evolutionary algorithms. It’s well-documented and ideal for those looking to experiment with GA.
- IEEE Xplore Digital Library
IEEE Xplore is a great resource for the latest research on optimization techniques, including conference papers, journals, and technical articles on PSO, GA, and SA in various fields.
IEEE Xplore - The Genetic and Evolutionary Computation Conference (GECCO)
GECCO is an annual conference that publishes cutting-edge research on genetic algorithms and evolutionary computation, offering presentations, papers, and resources on the latest GA applications.
GECCO Conference - Optimization Online
This open-access repository provides research articles, tutorials, and papers on a range of optimization techniques, including metaheuristics. It’s an ideal resource for finding the latest advancements and methods.
Optimization Online