Reducing the dimensionality of data can be the difference between seeing a pattern or missing it entirely. But with so many dimensionality reduction techniques available, it’s not always clear which to use.
Here, we’ll explore PCA, t-SNE, and UMAP, three powerful techniques for simplifying data while retaining its structure.
What Is Dimensionality Reduction?
Dimensionality reduction is a technique in machine learning and data analysis used to decrease the number of variables, or features, in a dataset. High-dimensional data can be difficult to work with and often contains redundant or irrelevant information. By reducing dimensions, we can visualize complex data more easily, speed up processing, and improve the performance of machine learning models.
Benefits of Dimensionality Reduction:
- Easier visualization of data patterns
- Improved model accuracy by removing noise
- Reduced computation time for machine learning algorithms
PCA: Principal Component Analysis
Principal Component Analysis (PCA) is one of the oldest and most widely used dimensionality reduction methods. It works by transforming the data into a new coordinate system, where each axis, or “principal component,” represents the direction of maximum variance.
How PCA Works
PCA calculates linear combinations of the original features that maximize variance, creating new “principal components.” The first component explains the most variance in the data, the second component explains the second-most, and so on.
Strengths of PCA
- Fast and computationally efficient, even with large datasets
- Provides a clear mathematical interpretation of data variance
- Works well for linearly separable data where the features have a linear relationship
Limitations of PCA
- Limited with non-linear data structures
- Doesn’t always capture complex patterns or clusters
- Can be sensitive to scaling of the data
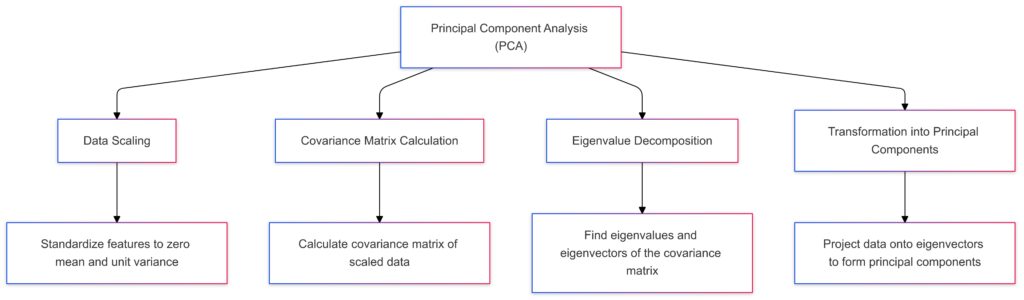
Data Scaling: Standardizes features to have zero mean and unit variance.
Covariance Matrix Calculation: Calculates the covariance matrix of the scaled data.
Eigenvalue Decomposition: Finds eigenvalues and eigenvectors of the covariance matrix.
Transformation into Principal Components: Projects data onto eigenvectors to form principal components, enabling dimensionality reduction.
Each step shows the progressive transformation of the data, emphasizing how PCA reduces dimensionality.
When to Use PCA: If your data is relatively simple, with linearly related features, PCA is a great choice. It’s also ideal for exploratory analysis when you want to quickly understand the primary directions of variability in the data.
t-SNE: t-Distributed Stochastic Neighbor Embedding
t-Distributed Stochastic Neighbor Embedding (t-SNE) is a popular method for visualizing high-dimensional data in two or three dimensions. It’s especially favored for its ability to capture complex, non-linear relationships in data.
How t-SNE Works
t-SNE uses a probabilistic approach to preserve the distances between points in the high-dimensional space. It places similar points closer together in the reduced space and places dissimilar points farther apart, revealing clusters that might otherwise remain hidden.
Strengths of t-SNE
- Excels at visualizing clusters in data
- Captures non-linear relationships, making it ideal for complex datasets
- Works well on sparse data, like word embeddings or genetic data
Limitations of t-SNE
- High computational cost, especially with large datasets
- Results can vary depending on hyperparameters like perplexity and learning rate
- Does not retain the global structure as well as other methods
When to Use t-SNE: t-SNE is well-suited for data that likely contains distinct clusters or groups, like image data or text embeddings. It’s best used for visualization and exploration, especially when you suspect the data has non-linear separations.
UMAP: Uniform Manifold Approximation and Projection
Uniform Manifold Approximation and Projection (UMAP) is a relatively new method that’s gained traction as an effective alternative to t-SNE. Developed with a focus on both local and global structure, UMAP balances interpretability, speed, and scalability.
How UMAP Works
UMAP uses mathematical concepts from topology to preserve the high-dimensional structure of data, making it ideal for creating low-dimensional representations that reflect the data’s intrinsic relationships. It’s faster than t-SNE, making it a good choice for larger datasets.
Strengths of UMAP
- Faster than t-SNE on larger datasets
- Balances local and global structure, retaining more overall information
- Works with both sparse and dense data, and can often capture both large-scale trends and fine-grained details
Limitations of UMAP
- Hyperparameters can influence results, though they’re easier to tune than t-SNE
- Not as widely tested across all domains compared to PCA and t-SNE
- Interpretation may be complex due to mathematical underpinnings
When to Use UMAP: UMAP is a great choice for applications that require speed and scalability, such as processing large biological datasets, image embeddings, or high-dimensional spatial data. It’s particularly effective when both local and global structures are important.
Comparing PCA, t-SNE, and UMAP
Each of these methods shines in specific scenarios. Here’s a quick comparison to help you make the best choice:
| Feature | PCA | t-SNE | UMAP |
|---|---|---|---|
| Computation Speed | Fast | Moderate to Slow | Fast |
| Complexity | Simple | High | Moderate |
| Non-Linear Data Handling | Limited | Strong | Strong |
| Interpretability | High | Moderate | Moderate |
| Global Structure | Preserved | Limited | Better than t-SNE |
| Hyperparameter Tuning | Minimal | Essential | Moderate |
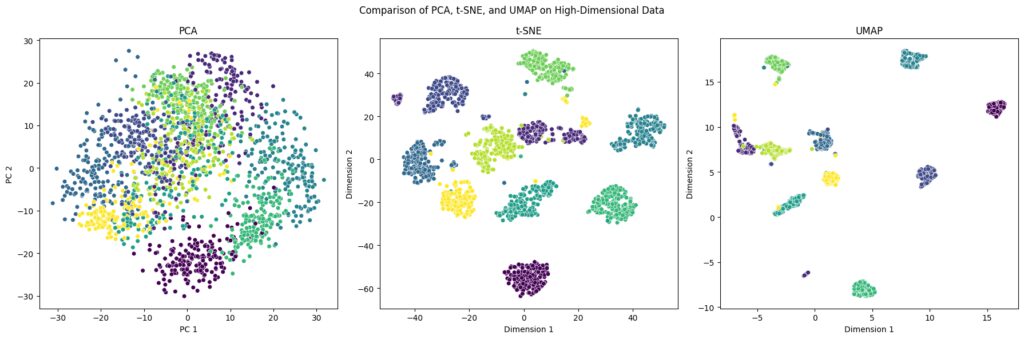
t-SNE projects data with a focus on local clustering.
UMAP aims to preserve both local and global structures in the data.
Choosing the Best Technique for Your Data
When it comes to choosing the right dimensionality reduction technique, think about what you value most: interpretability, speed, or the ability to capture non-linear patterns.
- Go with PCA if you need a quick, interpretable solution that works well for linearly related data.
- Use t-SNE when working with complex, clustered data and you want a strong, detailed visualization.
- Choose UMAP for large datasets or when both local and global structure matter, like in biological or text data.
In many cases, it’s worth trying out both t-SNE and UMAP side-by-side, especially if you’re unsure which one will best represent your data’s structure.
Practical Examples of PCA, t-SNE, and UMAP in Action
To understand the unique strengths of each technique, let’s look at some practical examples of how PCA, t-SNE, and UMAP are applied in real-world scenarios. From image processing to recommendation systems, these techniques reveal insights that otherwise remain hidden in high-dimensional data.
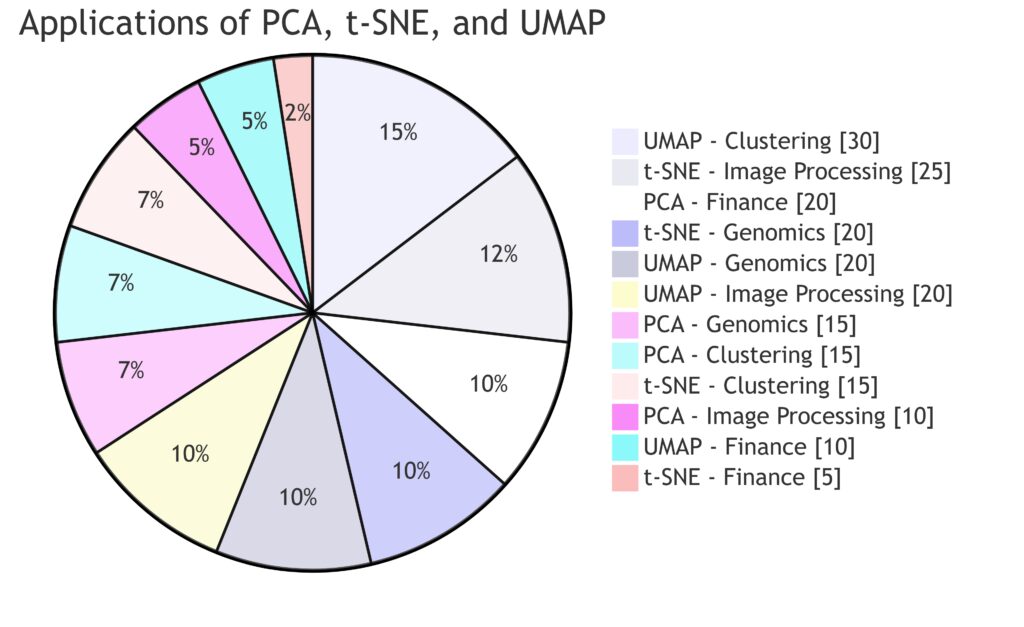
Finance, Genomics, Image Processing, and Clustering each have segments that highlight the relevance of each technique.
PCA is widely used in finance, t-SNE excels in image processing, and UMAP is prominent in clustering and genomics.
This chart visualizes how each technique aligns with specific application areas.
PCA in Financial Data Analysis
In finance, datasets often have numerous features like stock prices, trading volumes, and various financial indicators. PCA is frequently used to reduce dimensionality, retaining only the most significant features to analyze overall trends in the market.
How PCA Helps in Finance
By using PCA, analysts can simplify the feature space and focus on principal components that explain most of the variance, such as factors related to overall market sentiment or sector-based trends. This reduction improves computational efficiency for algorithmic trading or risk assessment models.
Example Use Case
In a portfolio optimization context, PCA might reduce hundreds of asset returns into a smaller set of components, helping fund managers understand core factors that impact returns, without getting bogged down by individual stock fluctuations.
Key Takeaway: PCA is well-suited to financial data due to its emphasis on linear relationships and interpretability, making it easier to understand how broad economic factors impact individual assets.
t-SNE for Image and Text Clustering
When working with image or text data, which is typically high-dimensional, t-SNE offers unique advantages for capturing complex, non-linear patterns and creating intuitive visualizations that reveal groupings.
How t-SNE Excels in Clustering
In computer vision tasks, t-SNE can reduce the high-dimensional space of pixel data or embeddings to two or three dimensions, enabling a visual representation of image clusters. For text, t-SNE often helps cluster embeddings from word or sentence representations, helping us discover groupings in data, such as similar documents or sentiments.
Example Use Case
Suppose we have a dataset of hand-written digits or facial images. By applying t-SNE, we can produce a scatter plot where visually similar images form clusters, like grouping different digit classes (0-9) or arranging similar facial expressions near each other. Similarly, in natural language processing, t-SNE could reveal clusters of words with similar meanings based on word embeddings, aiding tasks like topic modeling.
Key Takeaway: t-SNE is ideal for visualization of clusters in image and text data, helping reveal structure and relationships that are not linearly separable.
UMAP for Genomics and Medical Data
UMAP has found a strong foothold in fields like genomics and biomedical research, where datasets are extremely high-dimensional and often require fast, reliable clustering while retaining both local and global patterns.
How UMAP Assists in Biomedical Fields
UMAP’s ability to handle sparse and non-linear data, while preserving both neighborhood relationships and some global structure, makes it valuable in analyzing complex biological data, such as genetic sequences, protein structures, or single-cell RNA sequencing.
Example Use Case
In single-cell genomics, UMAP can reduce thousands of gene expression features into a few dimensions, allowing researchers to visualize and interpret cell types or gene expression patterns. This is invaluable for understanding disease mechanisms, identifying new biomarkers, or finding potential therapeutic targets.
Key Takeaway: UMAP’s balance of computational efficiency, local and global structure preservation, and adaptability to non-linear data make it perfect for genomics and complex medical datasets where retaining structural integrity is crucial.
Best Practices for Implementing Dimensionality Reduction
Here are some best practices to keep in mind when choosing and applying these dimensionality reduction techniques.
Preprocessing and Data Scaling
- Normalize or Standardize: PCA and t-SNE can be sensitive to scaling, so it’s usually recommended to standardize features before applying them.
- Remove Outliers: Dimensionality reduction techniques, especially t-SNE, can sometimes be skewed by outliers, so it may help to clean the data beforehand.
- Feature Selection: If the dataset has too many features, it can be beneficial to perform basic feature selection first, reducing noise and improving interpretability.
Parameter Tuning and Experimentation
- Experiment with Parameters: t-SNE’s perplexity and learning rate, and UMAP’s nearest neighbors and minimum distance parameters, can drastically affect results. Try a few values to find what best represents your data.
- Multiple Trials: Especially with t-SNE, running multiple trials with different random seeds can yield more stable results, as t-SNE’s output can vary.
Use Visualization to Validate Results
Dimensionality reduction techniques often produce visualizations that can be interpreted intuitively. Use these visualizations to assess if the technique is capturing the expected structure.

Data Standardization: Ensures consistent scaling.
Remove Outliers: Cleans data for accurate analysis.
Feature Selection: Reduces dimensionality, focusing on relevant features.
Parameter Tuning: Refines settings for optimal performance.
Optional branches allow revisiting each stage if necessary, promoting iterative refinement for the best results.
Summary: Making the Choice Between PCA, t-SNE, and UMAP
Choosing the right dimensionality reduction technique is all about balancing simplicity, interpretability, and computational requirements.
- For quick, linear data exploration, PCA is a solid, interpretable choice.
- For complex, non-linear data with clusters, t-SNE’s visualizations are highly valuable, especially for medium-sized datasets.
- For large-scale data where both global and local structure matter, UMAP provides an ideal blend of efficiency and performance.
Whether working with financial data, images, or biological samples, choosing the right dimensionality reduction technique can turn overwhelming datasets into insightful visualizations and analyses.
FAQs
Why are t-SNE and UMAP preferred for data with complex clusters?
t-SNE and UMAP are designed to capture non-linear relationships, making them effective for data with intricate clusters, such as in image or text embeddings. These techniques reveal structures that linear methods like PCA can’t, which is why they are favored in applications involving pattern recognition, like clustering handwritten digits or word embeddings.
Can I use these techniques interchangeably, or are they specific to certain types of data?
While there is some overlap, each technique has strengths suited to particular types of data. For example, PCA is optimal for linearly separable data, while t-SNE and UMAP are better for non-linear, complex data. UMAP, with its scalability, is especially useful for large datasets. In practice, it’s common to experiment with more than one technique to see which provides the best results for a specific dataset.
Do these methods require hyperparameter tuning?
Yes, hyperparameter tuning can improve the results, especially for t-SNE and UMAP. In t-SNE, the perplexity and learning rate significantly impact clustering outcomes, while UMAP benefits from adjusting parameters like nearest neighbors and minimum distance. PCA, however, requires minimal tuning, typically only setting the number of components.
What are the limitations of each method?
PCA is limited to linear transformations and may miss non-linear relationships, making it less effective for clustering complex data. t-SNE, while effective for capturing local clusters, can be computationally intensive and sometimes inconsistent across runs. UMAP, though faster and versatile, may be challenging to interpret without an understanding of its mathematical foundations.
Is one of these techniques best suited for data visualization?
t-SNE and UMAP are both widely used for data visualization due to their ability to reveal underlying patterns and clusters in complex data. t-SNE is popular for visualizing well-separated clusters in 2D or 3D, while UMAP’s balance of local and global structure can provide more interpretable insights, especially with large datasets.
How do I decide on the right number of dimensions to reduce to?
The number of dimensions to reduce to depends on your data and goals. For PCA, a common approach is to choose enough components to capture a set percentage of the total variance (e.g., 90-95%). In t-SNE and UMAP, the dimensionality is typically reduced to 2 or 3 for visualization purposes. In other applications, testing several values can help determine what dimensionality offers the best balance between clarity and information retention.
Can PCA, t-SNE, and UMAP be used for unsupervised learning?
Yes, these techniques are often used in unsupervised learning to simplify data, allowing clustering algorithms to work more effectively. By reducing data complexity, they can enhance the performance of unsupervised methods like K-means clustering or hierarchical clustering, which may struggle with high-dimensional data. UMAP and t-SNE, in particular, are valuable for exploring natural groupings within data before applying clustering algorithms.
What should I know about pre-processing before using PCA, t-SNE, or UMAP?
Data standardization or normalization is often essential before applying these techniques, especially for PCA, as it can be sensitive to feature scaling. Normalization helps ensure that no single feature disproportionately influences the results. Removing outliers and handling missing values are also recommended, as these factors can distort the dimensionality reduction process, especially for t-SNE and UMAP.
Are there specific use cases where UMAP is better than t-SNE?
Yes, UMAP is generally faster than t-SNE and tends to perform better with large datasets. UMAP is also preferred when the data’s global structure (overall shape and relationships) is important, as it retains more of this structure than t-SNE. This makes UMAP ideal for fields like genomics, biomedical data analysis, and large-scale text embeddings, where data volumes and both local and global relationships matter.
How does computational cost compare among PCA, t-SNE, and UMAP?
PCA is typically the least computationally intensive, especially on large datasets, as it relies on straightforward matrix decompositions. t-SNE is the most computationally demanding, particularly with higher-dimensional and large datasets, as it requires calculating and optimizing distances between points multiple times. UMAP’s computational cost is generally lower than t-SNE and can scale more efficiently, making it a faster choice for large datasets without sacrificing too much detail.
Can these methods be combined with supervised learning techniques?
Absolutely. Dimensionality reduction techniques like PCA, t-SNE, and UMAP can enhance supervised learning models by reducing noise and irrelevant features. For example, PCA is frequently applied to preprocess features for classifiers or regression models. However, t-SNE and UMAP are generally used more for visualization and exploratory analysis, as they don’t necessarily preserve information in a way that’s optimal for downstream supervised tasks.
What are the most common applications of PCA, t-SNE, and UMAP?
PCA is frequently used in financial data analysis, feature reduction for machine learning models, and signal processing. t-SNE is commonly applied in image and text data clustering and pattern recognition, particularly where cluster visualization is important. UMAP is widely used in genomics, biomedical research, and any application where large, high-dimensional datasets need to be both visualized and clustered effectively.
Do dimensionality reduction techniques affect model interpretability?
Yes, dimensionality reduction can impact interpretability. PCA is highly interpretable, as each component represents a linear combination of original features, making it clear how each feature contributes to the data’s variance. However, t-SNE and UMAP are less interpretable because they focus on preserving relationships between points rather than original feature meanings, which can make it harder to trace results back to specific features.
Can dimensionality reduction help improve model accuracy?
In many cases, dimensionality reduction can indeed improve model accuracy by removing noise and irrelevant features. This is especially true for PCA, where irrelevant dimensions that add variance without meaningful information can be removed, making the model more efficient and accurate. However, if too much relevant information is removed, it can also hurt accuracy, so careful experimentation with dimensionality is essential.
Resources
Articles & Tutorials
- PCA Tutorial from DataCamp
Understanding PCA with Python
This beginner-friendly tutorial walks through PCA with Python code examples and visualizations, making it easy to understand and implement on real data. - t-SNE for Exploratory Data Analysis from Towards Data Science
How to Use t-SNE Effectively
This article explains how t-SNE works and provides tips for tuning hyperparameters for different datasets. It’s a practical guide to making the most of t-SNE visualizations. - UMAP Documentation and Tutorials
UMAP Documentation
The official UMAP documentation includes practical examples, tutorials, and in-depth explanations of UMAP’s underlying math. Ideal for those who want to fully understand and utilize UMAP in their own projects.
Courses & Online Lectures
- Coursera – “Unsupervised Learning, Clustering, and PCA” by the University of Washington
Course Link
This course covers essential unsupervised learning methods, including PCA, with a focus on practical application. It’s suited to learners at an intermediate level with some machine learning background. - Fast.ai’s Practical Deep Learning for Coders
Course Link
Fast.ai’s course includes dimensionality reduction techniques, with an emphasis on using UMAP and t-SNE in the context of deep learning applications like image and text embeddings.
Software Documentation
- Scikit-Learn Documentation for PCA and t-SNE
Scikit-Learn PCA
Scikit-Learn t-SNE
Scikit-Learn is a popular Python library for machine learning, and its documentation provides detailed explanations of how to use PCA and t-SNE, along with parameter options and examples. - UMAP for Python (UMAP-learn)
UMAP-learn GitHub Repository
This repository contains the UMAP implementation in Python, including installation instructions, examples, and community contributions. It’s an excellent resource for both learning and applying UMAP to real data.
Research Papers
- PCA: “The Singular Value Decomposition and Its Use in PCA” by I.T. Jolliffe
A classic paper on PCA, explaining the method and its applications in various fields. This is a foundational read for those wanting a deeper theoretical understanding. - t-SNE: “Visualizing Data using t-SNE” by Laurens van der Maaten and Geoffrey Hinton
Paper Link
This is the original paper introducing t-SNE, co-authored by machine learning pioneer Geoffrey Hinton. It dives deep into the math and logic behind t-SNE, making it a key resource for in-depth study. - UMAP: “UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction” by Leland McInnes, John Healy, and James Melville
Paper Link
This paper introduces UMAP, describing the topological concepts that form the basis of the technique and detailing its performance in comparison to other methods.
