Quantum Machine Learning (QML) combines the principles of quantum computing and machine learning to process and analyze data in ways classical systems cannot.
One particularly intriguing tool in this field is the Restricted Boltzmann Machine (RBM)—a neural network model renowned for its simplicity and its ability to uncover hidden patterns. In QML, RBMs serve a dual purpose: acting as machine learning tools and facilitating quantum-inspired data processing.
But what exactly are RBMs, and why are they central to this innovation?
What Are Restricted Boltzmann Machines (RBMs)?
The Basics of RBMs
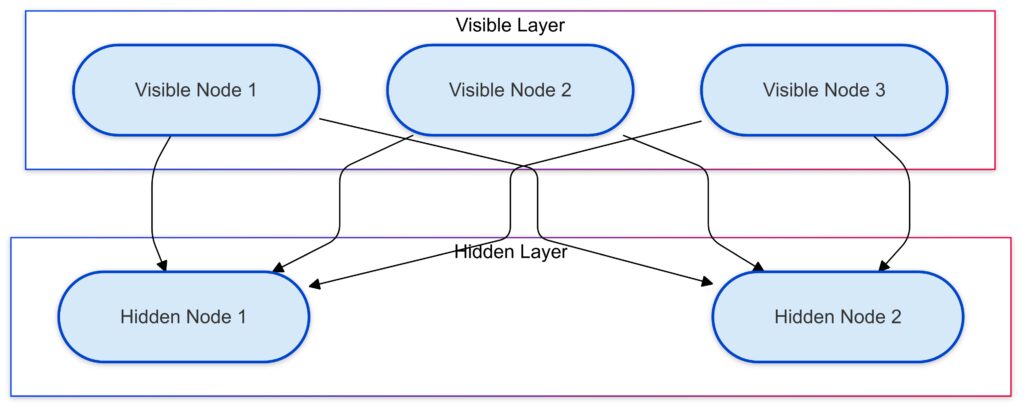
At their essence, RBMs are stochastic neural networks used to model patterns in data. Unlike typical neural networks, RBMs consist of just two layers:
- Visible layer: Represents input data like images or numerical values.
- Hidden layer: Captures complex patterns and relationships in the data.
The two layers are fully connected but lack intra-layer connections, making RBMs “restricted.” This structure simplifies computations and enables efficient unsupervised learning.
How RBMs Learn Data Patterns
RBMs learn by adjusting the weights connecting visible and hidden layers. This process is achieved using contrastive divergence, a learning method that minimizes the difference between observed and modeled data distributions.
RBMs vs Traditional Neural Networks
RBMs stand apart because they:
- Focus on unsupervised learning (perfect for clustering or anomaly detection).
- Model probabilities instead of deterministic mappings.
- Are naturally suited for quantum enhancements due to their probabilistic nature.
Why RBMs Matter in Quantum Machine Learning
A Perfect Fit for Quantum Mechanics
Quantum systems operate probabilistically, much like RBMs. This inherent compatibility allows quantum RBMs (QRBMs) to thrive in quantum computing environments, leveraging quantum superposition and entanglement for superior performance.
Quantum Speedup in Training
Traditional RBMs face challenges when scaling to massive datasets. Quantum computing mitigates this issue by exponentially accelerating calculations, such as probability estimations and weight adjustments. This is crucial in training large-scale RBMs efficiently.
Revolutionizing Data Representation
RBMs play a critical role in encoding quantum data into forms suitable for machine learning. Quantum computers use RBMs to represent quantum states compactly, reducing computation overhead while preserving data integrity.
Applications of RBMs in Quantum Domains
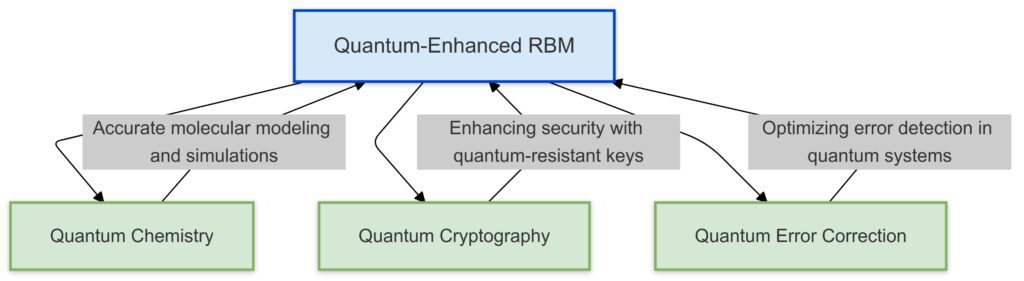
Quantum Chemistry
RBMs help analyze molecular structures by learning quantum wave functions. This insight advances drug discovery and material science research.
Quantum Error Correction
In quantum computing, maintaining error-free computation is vital. RBMs assist in detecting and correcting errors in quantum gates and processes.
Quantum Cryptography
Security is at the heart of future technologies. RBMs enable efficient modeling of secure quantum channels for cryptographic systems, boosting security in communication protocols.
Key Challenges for RBMs in Quantum Machine Learning
Scalability
Despite quantum speedup, training QRBMs on high-dimensional data remains computationally expensive. Developing scalable quantum architectures is a work in progress.
Noise Sensitivity
RBMs rely on precise calculations, but quantum systems are notoriously prone to noise and decoherence. Addressing this challenge requires advanced noise-reduction techniques.
Resource Intensity
Quantum computers are still in their infancy. Building and operating them is costly, limiting the accessibility of QRBM implementations for researchers and developers.
How RBMs Transform Quantum Optimization
Tackling Complex Optimization Problems
RBMs are integral to solving optimization problems in quantum computing. These problems, such as minimizing energy states in physics or optimizing logistics routes, involve finding the best solution among numerous possibilities. QRBMs leverage quantum tunneling and probabilistic sampling to find these solutions faster and more effectively than classical methods.
Bolstering Variational Quantum Algorithms
Variational quantum algorithms (VQAs) rely on optimizing quantum states to solve real-world problems. QRBMs provide a robust framework for modeling and optimizing quantum systems in VQAs, enhancing their efficiency and accuracy.
Bridging the Gap Between Classical and Quantum Models
While purely quantum systems are still evolving, hybrid quantum-classical models combine classical RBMs with quantum computing power. This synergy allows for more scalable and practical applications in areas like machine learning and optimization.
Cutting-Edge Research and Advancements
Deep Quantum Neural Networks
Researchers are developing deep quantum neural networks (DQNNs) by stacking multiple QRBMs. These deeper architectures promise groundbreaking improvements in pattern recognition and decision-making tasks across quantum datasets.
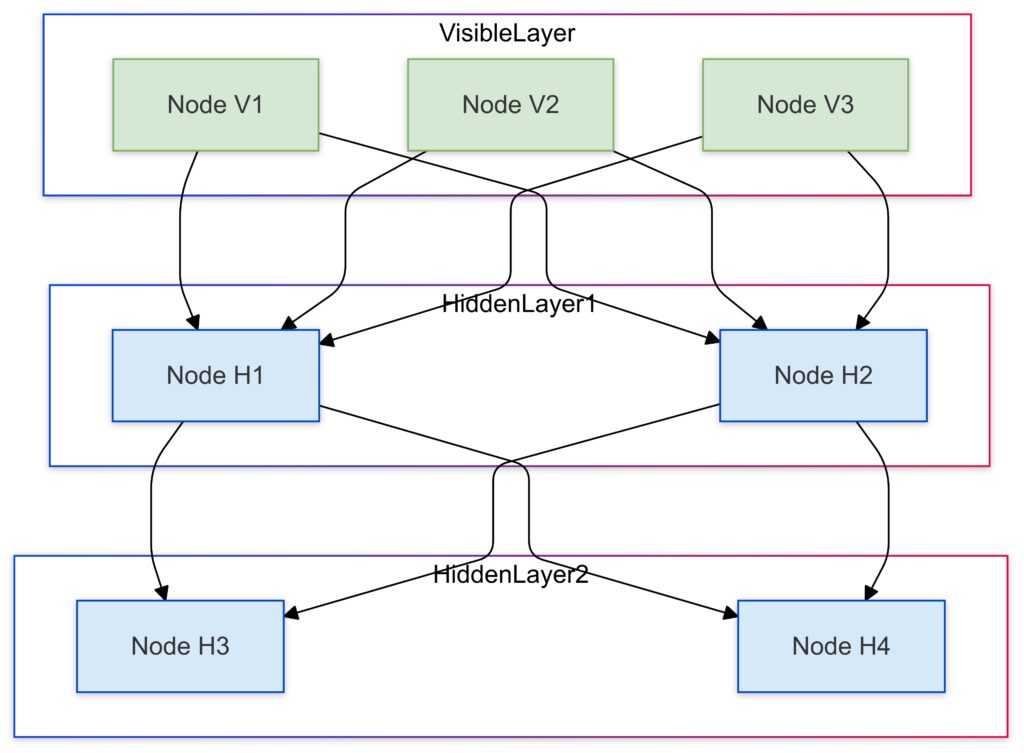
This diagram illustrates the architecture of a Deep Boltzmann Machine (DBM) adapted for quantum systems:
Novel Training Methods
Traditional training methods like contrastive divergence are evolving with quantum-specific algorithms. Quantum-aware optimizers, such as quantum gradient descent, are paving the way for faster and more accurate training of QRBMs.
Advances in Hardware Integration
Quantum hardware innovations, such as those from IBM and Google, are enabling better implementation of QRBMs. Enhanced qubit stability and increased quantum circuit depth are allowing QRBMs to tackle larger datasets and more complex tasks.
Industry Applications Driving Quantum Machine Learning
Healthcare and Drug Discovery
RBMs in quantum systems are revolutionizing personalized medicine and drug research. They allow researchers to model biological systems at the quantum level, leading to faster drug simulations and reduced development time.
Financial Modeling
RBMs are tackling challenges in risk assessment and market predictions by accurately modeling financial data. The probabilistic capabilities of QRBMs align perfectly with the inherent uncertainties in financial markets.
Climate Modeling
As climate science grows more data-intensive, RBMs assist in simulating climate patterns and identifying trends. Quantum enhancements allow researchers to process massive datasets with higher precision.
Autonomous Systems
From self-driving cars to drones, RBMs are improving decision-making processes in autonomous systems. Quantum computing accelerates the real-time learning needed for such applications.
Quantum Hardware: Supercharging RBM Performance
Quantum Annealers: A Natural Partner for RBMs
Quantum annealers, such as those developed by D-Wave, are purpose-built for solving optimization problems. These machines align perfectly with RBMs’ probabilistic nature, enabling faster training and inference. Specifically:
- Energy-based models like RBMs benefit from quantum annealers’ ability to explore large solution spaces efficiently.
- Quantum annealers minimize energy states in RBMs, achieving rapid convergence on optimal solutions.
For instance, D-Wave has already demonstrated the ability to solve complex machine learning problems using hybrid RBM frameworks.
Universal Quantum Computers for Flexibility
Universal quantum computers, such as IBM’s Quantum or Google’s Sycamore, offer more flexibility than annealers. By supporting arbitrary quantum circuits, these machines can implement quantum-enhanced RBMs for diverse applications, including:
- Real-time data modeling.
- Variational quantum simulations for advanced RBM training.
Hardware-Specific Enhancements
Quantum hardware providers are continuously addressing limitations that affect RBM performance. Key improvements include:
- Error-correction protocols: Mitigate decoherence and noise to preserve data fidelity in QRBM operations.
- Increased qubit counts: Allow QRBMs to model larger, more complex datasets effectively.
- High-connectivity architectures: Boost communication between qubits to simulate intricate RBM structures.
As quantum hardware matures, it’s expected to unlock entirely new use cases for RBMs in fields like quantum natural language processing and real-time optimization.
Theoretical Innovations in Quantum RBMs
Quantum Enhanced Contrastive Divergence
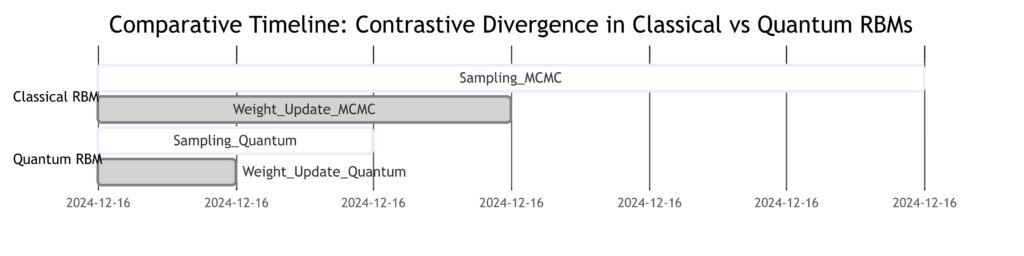
Traditional RBMs rely on contrastive divergence (CD) to approximate gradients and adjust weights, but this can be computationally intensive for complex datasets. Recent theoretical advancements integrate quantum algorithms to enhance this process:
- Quantum Gibbs Sampling: By leveraging quantum superposition, RBMs can sample from complex probability distributions faster than classical methods.
- Variational Monte Carlo Methods: These techniques use quantum circuits to improve the efficiency of CD, especially in high-dimensional spaces.
This quantum enhancement significantly reduces training time while preserving the accuracy of learned patterns.
Quantum-State Representations in RBMs
A breakthrough in RBM theory is their ability to represent quantum wavefunctions. In this context:
- RBMs are used as compact representations of complex quantum many-body systems, an essential tool in quantum chemistry and condensed matter physics.
- Hybrid models combine RBMs with tensor networks, extending their representational power while maintaining computational efficiency.
For example, RBMs have been applied to approximate the ground-state wavefunctions of spin systems, outperforming traditional methods in accuracy and scalability.
Boltzmann Machines and Quantum Variational Circuits
The fusion of RBMs with variational quantum circuits (VQCs) represents a significant theoretical leap. VQCs replace classical hidden layers in RBMs with quantum circuits, offering benefits such as:
- Increased expressiveness: Quantum circuits capture intricate dependencies in data that classical RBMs struggle to model.
- Adaptive training: The combination of RBMs with quantum variational algorithms optimizes energy landscapes for applications like quantum chemistry and optimization.
This hybridization opens doors to solving non-trivial problems in physics and machine learning with unprecedented precision.
Advanced RBM Architectures for QML
Deep Boltzmann Machines in Quantum Context
Deep Boltzmann Machines (DBMs) extend RBMs by introducing multiple hidden layers. Recent research adapts DBMs for quantum use, enabling:
- Hierarchical representation of quantum states.
- Enhanced scalability for learning multi-level quantum correlations.
Quantum-augmented DBMs are particularly promising for tasks like quantum state tomography, where reconstructing quantum states requires sophisticated models.
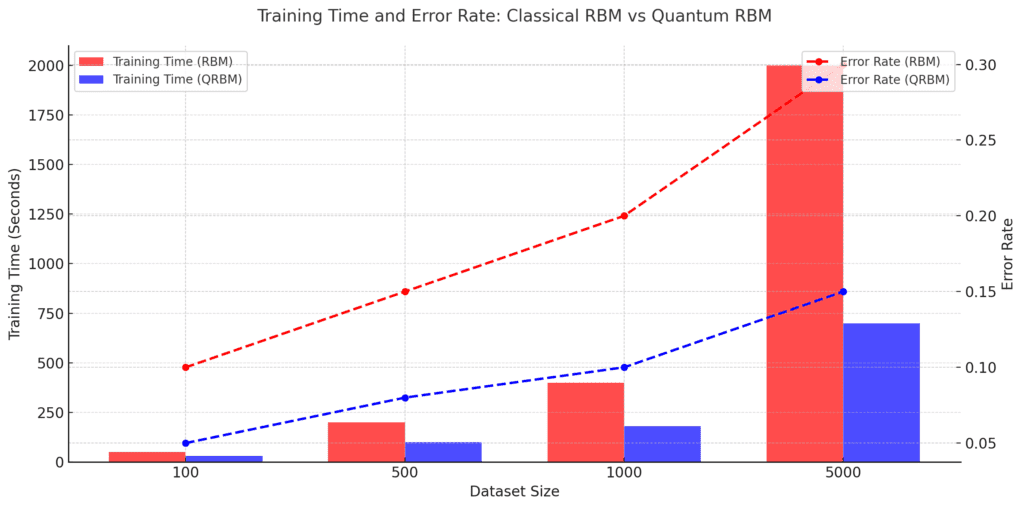
Time-Dependent Quantum RBMs
A cutting-edge concept involves time-dependent RBMs, which adapt their weights dynamically based on evolving quantum data. This approach is being explored for applications like:
- Dynamic systems modeling: Predicting outcomes in quantum systems over time.
- Adaptive quantum error correction: RBMs update their parameters in real time to correct quantum gate errors effectively.
The Role of Entanglement in QRBM Design
Entanglement—a uniquely quantum property—has profound implications for RBMs. Theoretical advancements focus on incorporating entanglement directly into RBM architectures, enabling:
- More efficient encoding of quantum correlations in data.
- Enhanced sampling algorithms to better model non-classical phenomena.
Researchers are exploring how entangled hidden layers can boost RBMs’ capacity to handle quantum datasets.
Emerging Mathematical Models for QRBMs
Quantum Probabilistic Graphical Models
RBMs are part of a broader family of probabilistic graphical models. Recent theoretical work generalizes these to the quantum domain, leading to:
- Quantum Factor Graphs: Enable probabilistic reasoning over quantum data.
- Hybrid Quantum-Classical Graphs: Bridge classical machine learning with quantum computing for practical scalability.
Improved Loss Functions for Quantum Training
Classical RBMs optimize weights using basic loss functions, like minimizing reconstruction error. Quantum RBMs introduce novel loss functions tailored to quantum tasks:
- Fidelity-based objectives: Measure the overlap between modeled and true quantum states, optimizing QRBMs for quantum system emulation.
- Energy-based losses: Directly target the Hamiltonian of quantum systems, aligning RBM training with physical principles.
These advances ensure that QRBMs are not just computationally efficient but also physically meaningful in quantum contexts.
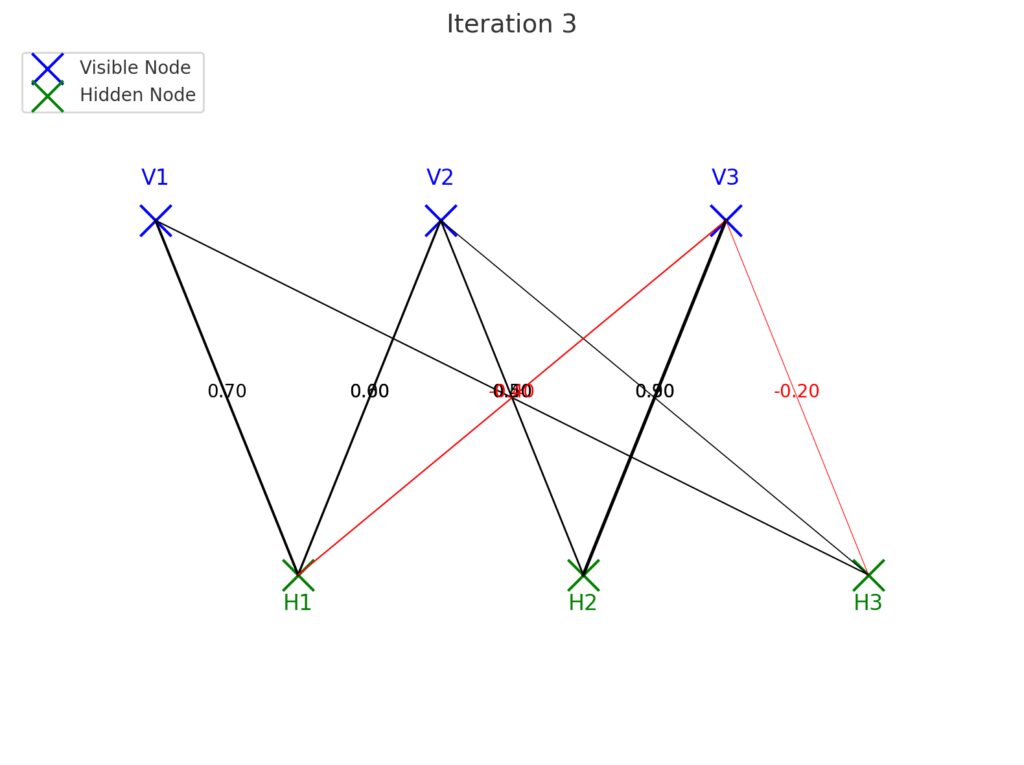
Iteration 1:
Initial weights are displayed as lines between the visible and hidden nodes.
Line thickness represents the magnitude of the weight, while color indicates the sign (red for negative, black for positive).
Iteration 2:
Weight values and connections are updated based on training progress.
Some weights grow stronger (e.g., V1 to H1), while others diminish or flip signs.
Iteration 3:
Final iteration shows further refinement in the weights.
Improved structure with stronger connections for significant relationships.
Potential Directions for Future Research
Recent experimental studies have demonstrated the practical integration of Restricted Boltzmann Machines (RBMs) with quantum computing, highlighting their potential in various applications.
Quantum Annealing for RBM Training
Researchers have employed quantum annealers, such as D-Wave’s systems, to train RBMs effectively. In one study, a hybrid quantum-classical approach was utilized to perform inference on RBMs. The D-Wave quantum annealer generated initial samples, which were then refined using classical Markov Chain Monte Carlo (MCMC) methods. This combination improved sampling efficiency and model performance, demonstrating the feasibility of integrating quantum annealing with classical processing for RBM training.
Quantum Image Denoising with RBMs
Another experimental application involved using RBMs for quantum image denoising. Researchers formulated the denoising task as a Quadratic Unconstrained Binary Optimization (QUBO) problem, suitable for quantum annealing. By balancing the distribution learned by a trained RBM with a penalty term for deviations from the noisy image, they achieved effective denoising. Testing on a D-Wave Advantage machine showed that this method could denoise binary images efficiently, indicating the potential of RBMs in quantum image processing tasks.
Hybrid Quantum-Classical Autoencoders
In the realm of quantum image compression and generative learning, a hybrid system combining classical deep neural network autoencoders with quantum annealing-based RBMs was explored. This approach achieved significant image compression, reducing 28×28 grayscale images to 6×6 binary images, with successful reconstruction. Additionally, the system generated new image samples that varied from the training data, showcasing the generative capabilities of quantum-enhanced RBMs.
These experimental results underscore the versatility and effectiveness of RBMs when integrated with quantum computing technologies, paving the way for advancements in machine learning, image processing, and data compression.
For those interested in practical implementations, an open-source project demonstrates the use of quantum annealing for RBMs on D-Wave’s quantum processing unit.
FAQs
Can RBMs be integrated with deep learning frameworks?
Yes, RBMs can act as building blocks for Deep Boltzmann Machines (DBMs), which are multi-layer networks. Quantum-augmented DBMs are being researched to enhance pattern recognition in high-dimensional quantum datasets.
In a recent experiment, quantum-enhanced DBMs were used to model the dynamics of quantum spin systems, achieving greater scalability compared to classical DBMs.
How do researchers test QRBMs in experimental settings?
QRBMs are tested using quantum processors like D-Wave’s quantum annealers or universal quantum computers from IBM or Google. For example, researchers modeled energy distributions for a set of quantum systems using RBMs on a D-Wave machine, showing improved accuracy and speed over classical simulators.
Another experiment involved training QRBMs on synthetic datasets to detect anomalies in quantum network traffic, proving their effectiveness in quantum cybersecurity.
How are RBMs used in unsupervised learning tasks?
RBMs excel at unsupervised learning, where the model learns patterns in data without labeled outputs. They are commonly applied to tasks like clustering, feature extraction, and anomaly detection.
For example, in image data, RBMs can learn to represent features such as edges or textures without being explicitly trained for these. In quantum machine learning, QRBMs are used to uncover hidden patterns in quantum system dynamics or optimize quantum circuit parameters.
Do RBMs only work with binary data?
Classical RBMs were initially designed for binary data, but extensions like Gaussian-Binary RBMs and Replicated Softmax RBMs can handle continuous or count-based data. In the quantum realm, QRBMs can represent complex-valued quantum states using additional mathematical transformations.
For instance, researchers used Gaussian-Binary RBMs to process quantum measurement data, representing continuous wavefunctions for quantum chemistry simulations.
Can RBMs be used for quantum state reconstruction?
Yes, one of the most promising applications of QRBMs is quantum state tomography—reconstructing quantum states from measurement data. RBMs learn a probabilistic model of the quantum state, simplifying the traditionally computationally expensive process.
For example, experiments have demonstrated that QRBMs can approximate the wavefunctions of multi-qubit systems, achieving high accuracy while using fewer resources than classical methods.
How are RBMs applied in generative tasks?
RBMs are powerful generative models that learn to produce new samples resembling the training data. This ability is leveraged in quantum machine learning to simulate quantum systems, generate synthetic datasets, and model probability distributions.
A practical example includes generating synthetic molecules in quantum chemistry, aiding researchers in identifying potential candidates for novel materials or drugs.
Are RBMs scalable for large datasets?
Scaling RBMs for high-dimensional data is a challenge, but quantum computing helps by accelerating sampling and reducing training time. Techniques like parallel quantum sampling enable RBMs to process large datasets more efficiently.
For instance, QRBMs have been tested on high-dimensional quantum datasets from particle physics, modeling distributions that would be infeasible for classical RBMs due to resource constraints.
How do RBMs contribute to quantum optimization?
RBMs are instrumental in solving quantum optimization problems, such as minimizing the energy of a system or optimizing quantum circuit parameters. They achieve this by modeling energy distributions and finding optimal configurations quickly.
For example, QRBMs have been applied in quantum variational algorithms, optimizing the parameters of quantum states for tasks like material design or portfolio optimization in finance.
Can RBMs integrate with reinforcement learning?
Yes, RBMs can be combined with quantum reinforcement learning (QRL) frameworks. They act as feature extractors or generative models, providing compact representations of the environment’s states and actions.
A notable experiment involved using QRBMs to assist a reinforcement learning agent in navigating a quantum maze, enabling it to find solutions more efficiently than with classical methods.
How do QRBMs handle quantum noise and errors?
Quantum systems are prone to noise, which can disrupt QRBM training and inference. Advanced QRBMs incorporate error mitigation techniques like noise-robust training algorithms and quantum error correction.
For example, researchers have developed QRBMs that dynamically adjust weights in response to noise patterns, improving performance in quantum annealers with noisy qubits.
How are RBMs linked to quantum cryptography?
In quantum cryptography, RBMs help model secure communication channels and detect vulnerabilities in quantum key distribution (QKD). They learn patterns in quantum signals to identify anomalies, ensuring robust security.
For example, QRBMs have been used in experiments to monitor quantum key distribution systems, flagging discrepancies caused by potential eavesdropping.
Are RBMs used in hybrid quantum-classical systems?
Yes, hybrid systems combine the strengths of quantum and classical computing. RBMs in these systems often act as classical components, while quantum processors accelerate specific tasks like sampling or optimization.
An example is the use of quantum-enhanced RBMs in hybrid models for climate data analysis, where classical RBMs preprocess the data and quantum components refine the patterns for forecasting.
Resources
Foundational Texts and Tutorials
- Deep Learning by Ian Goodfellow, Yoshua Bengio, and Aaron Courville
This book provides an excellent introduction to RBMs, their structure, and applications in traditional machine learning. It’s a must-read for understanding the basics.
Available here - Quantum Machine Learning: What Quantum Computing Means to Data Mining by Peter Wittek
This book bridges the gap between quantum computing and machine learning, including discussions on how RBMs fit into quantum contexts.
Buy on Amazon - Restricted Boltzmann Machines: A Step-by-Step Guide
A beginner-friendly online tutorial explaining how RBMs work, complete with code examples in Python.
Research Papers and Articles
- Learning with Boltzmann Machines: Advances and Challenges
An overview of RBMs, including recent quantum enhancements and challenges in applying them to large-scale problems.
Read on Springer - Quantum Boltzmann Machines for Machine Learning
This foundational paper discusses the theoretical framework for QRBMs and their potential for solving quantum data problems.
Read on arXiv - Hybrid Quantum-Classical Neural Networks with RBMs
A detailed exploration of hybrid RBM architectures combining classical deep learning techniques with quantum processors.
Read on arXiv
Online Courses and Tutorials
- IBM Quantum Experience
IBM offers free access to quantum computers and tutorials, including projects involving RBMs. Their quantum programming platform, Qiskit, is an excellent resource.
Explore IBM Quantum - Quantum Machine Learning by edX
A structured online course that covers quantum computing basics, quantum algorithms, and their applications in machine learning. - D-Wave Systems Developer Resources
D-Wave provides tools and guides for implementing RBMs using their quantum annealers, along with open-source libraries for hybrid quantum-classical models.
Open-Source Libraries and Tools
- TensorFlow and PyTorch
Both frameworks include implementations of RBMs. TensorFlow Quantum extends these capabilities to quantum machine learning tasks.
TensorFlow Quantum | PyTorch RBM Example - Ocean SDK by D-Wave
A comprehensive toolkit for developing applications on D-Wave’s quantum annealers, with example projects for RBMs. - QuTip: Quantum Toolbox in Python
A Python library for simulating quantum systems, useful for experimenting with QRBMs and quantum state tomography.
Explore QuTip
Community Forums and Events
- Stack Overflow
Search for questions related to RBMs and quantum machine learning or post your own queries.
Visit Stack Overflow - Quantum Computing Stack Exchange
A specialized community for discussing quantum computing topics, including QRBMs.
Visit Quantum Computing SE - Conferences and Workshops
- NeurIPS (Neural Information Processing Systems): Includes workshops on quantum machine learning.
- Qiskit Global Summer School: Annual event focused on quantum computing and its applications in machine learning.
- Quantum.Tech Conferences: Brings together experts from academia and industry to discuss quantum advancements.
Hands-On Projects and GitHub Repositories
- QRBM: A Quantum RBM Implementation
A GitHub project providing a practical implementation of QRBMs using Python and quantum computing tools like Qiskit.
View GitHub Repo - Quantum RBM Example with D-Wave
Demonstrates training RBMs on quantum annealers, with code and documentation.
View GitHub Repo - TensorFlow Quantum Tutorials
Contains examples of building and training quantum-enhanced models, including RBMs.
Visit GitHub