When it comes to optimization in linear programming (LP), two heavyweight methods dominate the conversation: Simplex and Interior-Point Methods. Each has its loyal followers and unique advantages, but which one is truly better?
Let’s dive into their mechanics, strengths, and use cases to find out.
What Are Simplex and Interior-Point Methods?
Simplex: The Classic Workhorse
The Simplex algorithm, developed by George Dantzig in 1947, is a staple in optimization. It systematically moves along the edges of the feasible region of a linear programming problem to find the optimal solution.
- Simplex operates on the geometry of the problem, focusing on vertices.
- It guarantees optimality by traversing neighboring vertices in a specific direction.
- Well-suited for problems where solutions are likely near boundary points.
For example, Simplex excels in cases where problems have few constraints but many variables, ensuring efficient navigation through the feasible space.
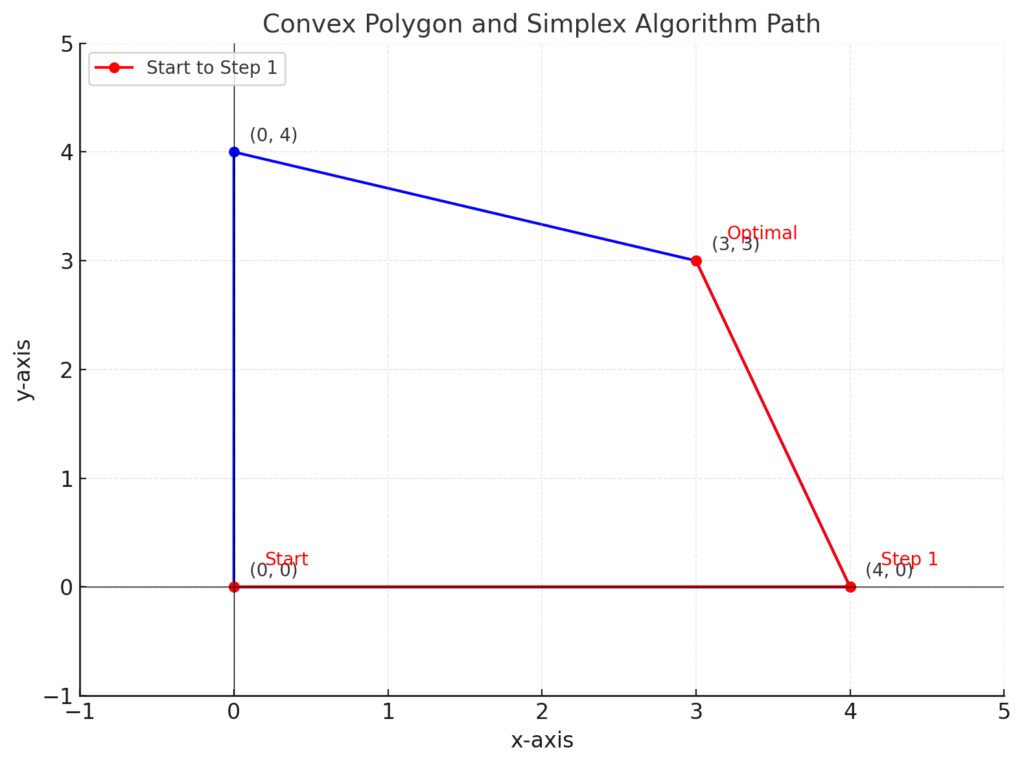
Blue Polygon: Represents the feasible region.
Vertices: Points defining the polygon, labeled with their coordinates.
Red Path: The progression of the Simplex algorithm, with labels marking each step:Start: The algorithm’s initial point.
Step 1: The first move along the edge.
Optimal: The final optimal solution.
Interior-Point Methods: A Modern Alternative
Interior-Point Methods (IPMs), introduced in the 1980s, revolutionized optimization by approaching the solution differently. Instead of navigating the edges, IPMs traverse the interior of the feasible region, gradually converging on the optimal solution.
- They leverage matrix factorization and numerical linear algebra.
- Often faster for large-scale LP problems with thousands or millions of variables.
- Best for scenarios where the problem structure is complex and dense.
These methods shine in applications like data science, machine learning, and other fields requiring high-dimensional optimization.
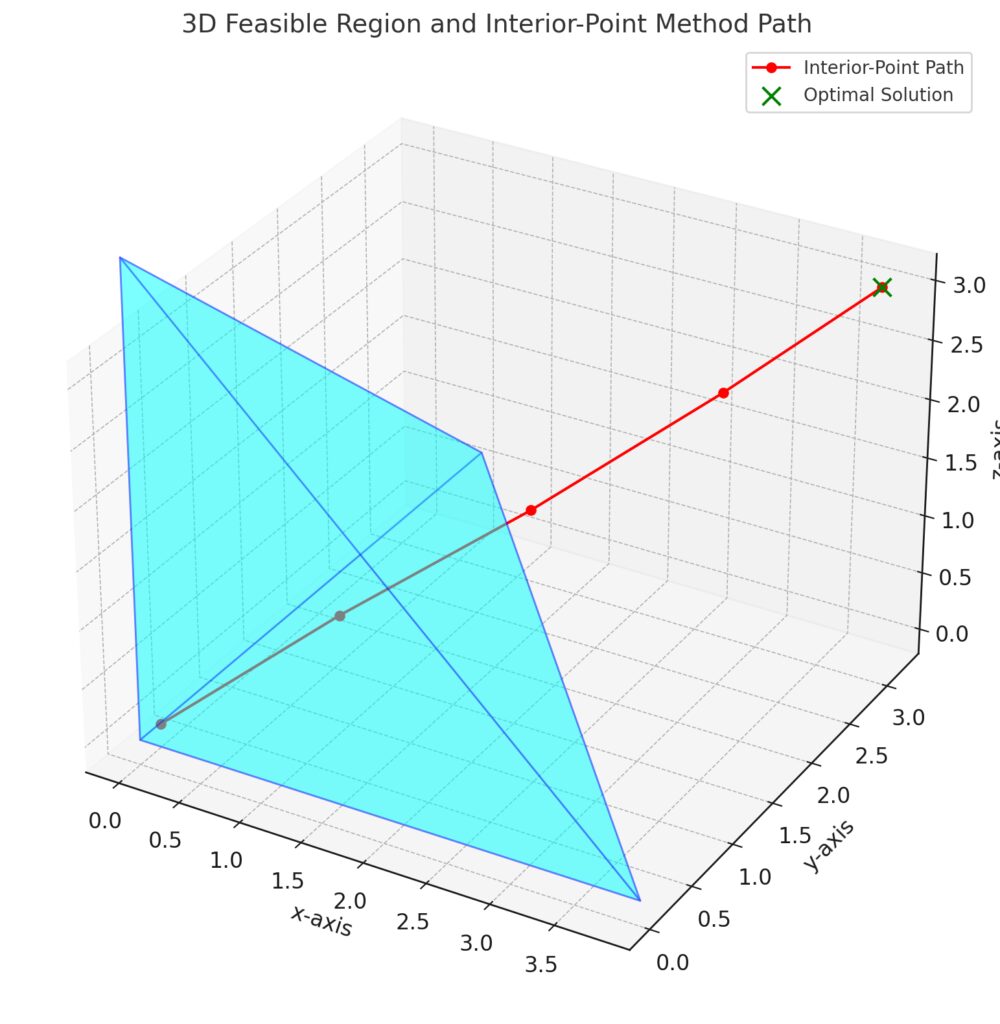
Feasible Region: Represented by a tetrahedron, which is the solution space for the linear programming problem. Interior-Point Path: Shown as a red curve through the interior of the feasible region, illustrating the method’s trajectory. Optimal Point: Highlighted in green, marking the final solution.
How Simplex Excels in Specific Cases
Simplicity and Interpretability
Simplex provides more than just results—it offers geometric intuition about the problem. You can see which constraints are binding and analyze the path to the solution.
- Edge-walking mechanism makes it highly transparent.
- Great for sensitivity analysis and post-optimality insights.
Simplex is especially handy in decision-making contexts, where managers might need to understand the why behind the results.
Speed for Small to Medium Problems
For smaller problems, Simplex can outperform IPMs due to lower computational overhead.
- Problems with sparse constraint matrices benefit from its streamlined edge navigation.
- Often yields an exact optimal solution faster than IPMs.
Robustness in Degenerate Problems
Degeneracy occurs when multiple solutions exist. Simplex handles these gracefully, offering reliable results, while IPMs may struggle with numerical instability in similar cases.
Interior-Point Methods for Large-Scale Optimization
Superior Scalability
Interior-Point Methods scale exceptionally well with large datasets. Their reliance on matrix factorization allows them to handle problems that would bog down Simplex.
- Better suited for large, dense problems.
- Efficient for solving quadratic and nonlinear programming problems.
For instance, network flow problems and high-dimensional machine learning models benefit immensely from IPMs’ speed and stability.
Numerical Stability
IPMs maintain numerical precision even in challenging scenarios, such as those involving ill-conditioned constraint matrices.
- Use sophisticated algorithms to manage precision loss.
- Avoid pitfalls like cycling, which can affect Simplex under certain conditions.
Real-World Applications
Interior-Point Methods dominate in industries where problem size and complexity are high. Examples include:
- Portfolio optimization in finance.
- Large-scale supply chain management.
- Electric grid optimization and load balancing.
Head-to-Head Performance: Key Factors to Consider
Problem Size and Structure
- Small or sparse problems: Simplex is the clear winner.
- Large, dense, or complex problems: Interior-Point Methods shine.
Speed and Memory Requirements
- Simplex can be faster for straightforward problems but requires more iterations for larger datasets.
- IPMs demand higher memory usage due to their reliance on matrix operations.
Solution Insights
If you need detailed sensitivity analysis or vertex-specific information, Simplex offers more interpretability. In contrast, IPMs often produce solutions without such granularity.
Comparing Performance Across Diverse Scenarios
Both Simplex and Interior-Point Methods have unique strengths, but their effectiveness depends on the context. Let’s break it down further.
Simplex for Practical Decision-Making
Resource Allocation Problems
Simplex is a go-to for industries that need practical, actionable insights. For example:
- Manufacturing: Optimizing production schedules under resource constraints.
- Logistics: Minimizing costs while meeting delivery deadlines.
The edge-traversal approach aligns well with these real-world constraints, offering clear corner-point solutions.
Business Environments with Small LP Models
When decision-makers deal with LP problems that involve a few constraints and many variables, Simplex’s interpretability and manageable overhead make it ideal. It’s often the tool of choice in:
- Financial planning.
- Marketing campaigns with budget constraints.
Interior-Point Methods in Computationally Intense Fields
High-Dimensional Applications
Interior-Point Methods excel in data-intensive environments, where constraints and variables scale dramatically. These include:
- Machine Learning: For tasks like support vector machines or sparse regression.
- Big Data Optimization: Solving LP problems with millions of variables.
The ability of IPMs to handle dense matrices with precision is indispensable in modern computational fields.
Engineering and Scientific Models
IPMs also play a pivotal role in optimizing systems that need continuous updates or involve nonlinear relationships:
- Energy Systems: Balancing supply and demand in real-time grid operations.
- Transportation Models: Reducing congestion using dynamic route adjustments.
The Role of Software and Hardware Advances
Simplex Software Implementations
Modern software, like CPLEX and Gurobi, optimizes Simplex with heuristics and preprocessing. These innovations make it faster for smaller-scale, sparse LP problems.
IPM Enhancements Through Parallel Computing
Interior-Point Methods have seen significant gains thanks to parallelized computing. This makes them faster and more scalable for:
- Cloud-based optimization.
- Distributed computing systems.
Hybrid Approaches
Some solvers, like MOSEK, combine both methods to deliver the best of both worlds. They start with IPMs for large-scale feasibility analysis and switch to Simplex for fine-tuning the optimal solution.
Choosing the Right Method: Decision Factors
Blue Points (Simplex Method): The Simplex Method is more efficient for smaller problem sizes.Orange Points (Interior-Point Method): The Interior-Point Method shows better efficiency as problem size increases.Threshold Line (Green): Indicates a transition point around a problem size of 100, where the preference may shift from Simplex to Interior-Point.
Key Questions to Guide Your Choice
- What’s the problem size? Small problems lean toward Simplex, while IPMs dominate in larger scales.
- Do you need interpretability? For in-depth sensitivity analysis, Simplex is unbeatable.
- Is speed critical? IPMs are better suited for high-dimensional, computationally intensive applications.
Emerging Trends in Optimization
With advances in machine learning integration and automated solver selection, future tools might blur the lines further. However, understanding these foundational methods ensures you choose the right approach today.
In the battle of Simplex vs. Interior-Point Methods, the answer isn’t one-size-fits-all. It’s about matching the method to the problem’s unique requirements. Choose wisely!
FAQs
Are there hybrid approaches combining the two methods?
Yes! Many modern solvers, like CPLEX or Gurobi, use hybrid algorithms. These start with Interior-Point Methods to quickly find a near-optimal solution and switch to Simplex for fine-tuning. For example, a machine learning hyperparameter tuning model might benefit from such hybrid approaches for faster, accurate results.
Which method is better for nonlinear programming?
Interior-Point Methods are more adaptable to nonlinear programming due to their reliance on advanced matrix operations. They are commonly used in quadratic programming and conic optimization problems, such as portfolio optimization in finance.
How do software tools implement these methods?
Most solvers like Gurobi, MOSEK, and MATLAB provide both methods. Simplex is often enhanced with heuristics for small LPs, while IPMs leverage parallelized computing for handling large-scale problems efficiently. For example, a global optimization task in cloud computing environments benefits from IPM implementations.
What are some industry-specific use cases?
- Simplex: Used in manufacturing for optimizing production plans and transportation for cost minimization.
- Interior-Point Methods: Common in data science for training models and in energy sectors for load distribution.
Can Simplex or Interior-Point Methods solve integer programming problems?
Neither method is inherently designed for integer programming (IP), which requires solutions to have integer values. However, they can be integrated into branch-and-bound or branch-and-cut algorithms. For instance:
- Simplex is often used in the relaxation phase to solve LP relaxations in mixed-integer programming (MIP) problems.
- Interior-Point Methods can assist in exploring feasible regions before branching.
An example is scheduling with binary decisions, like whether to open a facility (1) or keep it closed (0).
How do these methods compare in handling duality?
Both methods address dual problems effectively but in different ways:
- Simplex naturally provides dual variable values (shadow prices) as part of its solution, making it ideal for economic interpretations. For example, understanding the cost of constraints in resource allocation problems.
- Interior-Point Methods also solve the primal and dual simultaneously but may not offer the same level of interpretability. They’re often used in high-dimensional machine learning tasks, where dual insights are secondary to speed.
Which method is better for highly sparse constraint matrices?
Simplex performs better for sparse matrices because it works along the edges of the feasible region, requiring less computational effort.
- Example: In transportation problems, such as optimizing delivery routes for a few cities, constraint matrices tend to be sparse, making Simplex an excellent choice.
Interior-Point Methods, however, might struggle with sparsity due to their reliance on matrix factorizations, which could fill the sparse matrix during calculations.
What about problems with millions of variables and constraints?
Interior-Point Methods are better suited for massive-scale problems, as they handle dense computations more efficiently. Consider optimizing telecommunications network traffic or airline scheduling, where millions of constraints must be satisfied concurrently. Here, IPMs can reduce computational time significantly.
Are these methods affected by problem conditioning?
Yes, problem conditioning (how sensitive the solution is to changes in input data) plays a crucial role:
- Interior-Point Methods are more stable for well-conditioned problems but may face numerical difficulties with poorly conditioned ones.
- Simplex can navigate around numerical instabilities with pivoting strategies. For instance, in supply chain optimization, poorly scaled constraints might lead to inaccuracies with IPMs.
Can either method handle dynamic constraints?
Dynamic or time-varying constraints are challenging for both methods. However:
- Simplex can adapt iteratively by re-solving for each time step, making it feasible for real-time scheduling problems in manufacturing.
- Interior-Point Methods, paired with dynamic programming techniques, excel in fields like energy grid management, where time-dependent constraints are frequent.
How does hardware impact their performance?
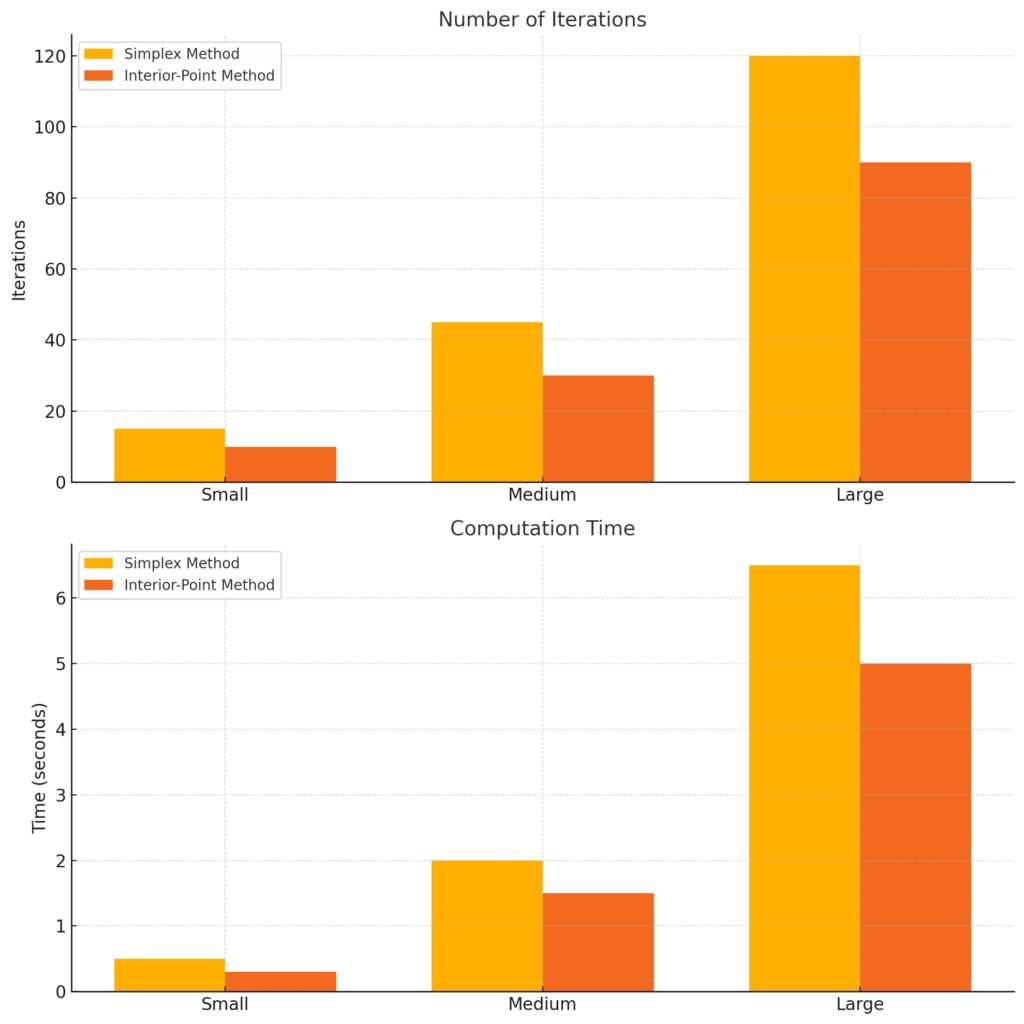
Number of Iterations:
- The Simplex Method generally requires more iterations compared to the Interior-Point Method.
- The difference becomes more pronounced as problem size increases.
Computation Time:
Both methods demonstrate an increase in computation time with larger problem sizes.
The Interior-Point Method shows faster computation times across all problem sizes.
- Simplex: Performs well on single-threaded architectures for smaller problems but struggles with parallelization. It thrives on traditional CPUs for routine business optimization tasks.
- Interior-Point Methods: Benefit significantly from parallel computing and GPU acceleration, making them ideal for solving high-dimensional problems in cloud environments.
Which method works better in stochastic optimization?
Interior-Point Methods have an edge in stochastic optimization due to their ability to handle large-scale scenarios and probabilistic models. For example, in financial risk management, IPMs can quickly solve models incorporating uncertainty about future events.
Are there specific academic or research applications for these methods?
- Simplex is often used in teaching and academic studies for its simplicity and interpretability. It provides an excellent foundation for learning optimization.
- Interior-Point Methods are popular in computational research, including areas like deep learning and operations research, where solving complex, large-scale problems is paramount.
Understanding these nuanced differences ensures that you not only pick the right method for the task but also maximize efficiency and insight in your optimization projects!
Resources
Books for In-Depth Study
- “Linear Programming and Network Flows” by Mokhtar S. Bazaraa, John J. Jarvis, and Hanif D. Sherali
This comprehensive text covers both Simplex and Interior-Point Methods, providing insights into linear programming and its applications in network flows. - “Primal-Dual Interior-Point Methods” by Stephen Wright
An essential resource focusing on primal-dual techniques within Interior-Point Methods, ideal for those seeking advanced knowledge in computational optimization. - “Understanding and Using Linear Programming” by Jiri Matousek and Bernd Gärtner
This approachable guide breaks down linear programming concepts, emphasizing the Simplex algorithm with intuitive examples.
Online Courses and Tutorials
- Optimization Specialization – Coursera
Offered by the University of Colorado Boulder, this series covers optimization fundamentals, including both Simplex and Interior-Point Methods, with practical applications. - MIT OpenCourseWare: Linear Programming
A free resource providing lecture notes and video lectures on linear programming, exploring the mathematical foundations of optimization methods. - Gurobi Optimization Tutorials
Learn to implement Simplex and Interior-Point Methods using Gurobi’s solver, with detailed examples in Python for hands-on learning.
Software Tools and Libraries
- CPLEX Optimization Studio
A widely used commercial solver implementing both Simplex and Interior-Point Methods, suitable for industrial-scale optimization problems. - Gurobi Optimizer
Known for high-speed performance, Gurobi provides APIs in multiple languages and includes hybrid algorithms combining Simplex and Interior-Point Methods. - SciPy (Python)
An open-source library with thelinprogfunction supporting Simplex and Interior-Point solvers, ideal for academic projects and small-scale problems. - MOSEK
A solver specializing in Interior-Point Methods for large-scale linear and conic optimization, widely used in finance and machine learning.
Research Papers and Articles
- “The Simplex Method for Linear Programming” by George B. Dantzig
A foundational paper introducing the Simplex algorithm, essential for understanding its origins and development. - “Karmarkar’s Algorithm for Linear Programming” by Narendra Karmarkar
This seminal paper introduced the first practical Interior-Point Method, revolutionizing linear programming optimization. - “Interior-Point Methods for Optimization” by Arkadi Nemirovski and Michael J. Todd
A comprehensive overview of Interior-Point Methods, discussing their development and application in large-scale optimization problems. ISyE Georgia Tech
Blogs and Practical Insights
- OR-Tools by Google
A blog and documentation hub for Google’s open-source optimization library, offering real-world examples of implementing optimization methods in logistics and scheduling. - Optimization at Gurobi
Gurobi’s blog includes case studies and technical write-ups, providing insights into choosing the best optimization methods for specific problems. - Towards Data Science (Medium)
This platform features practical guides on using Interior-Point Methods in Python and applying Simplex to real-world linear programming problems.