
What is a Support Vector Machine (SVM)?
A Support Vector Machine (SVM) is a supervised machine learning algorithm used for both classification and regression tasks. However, it’s primarily known for its prowess in classification problems.
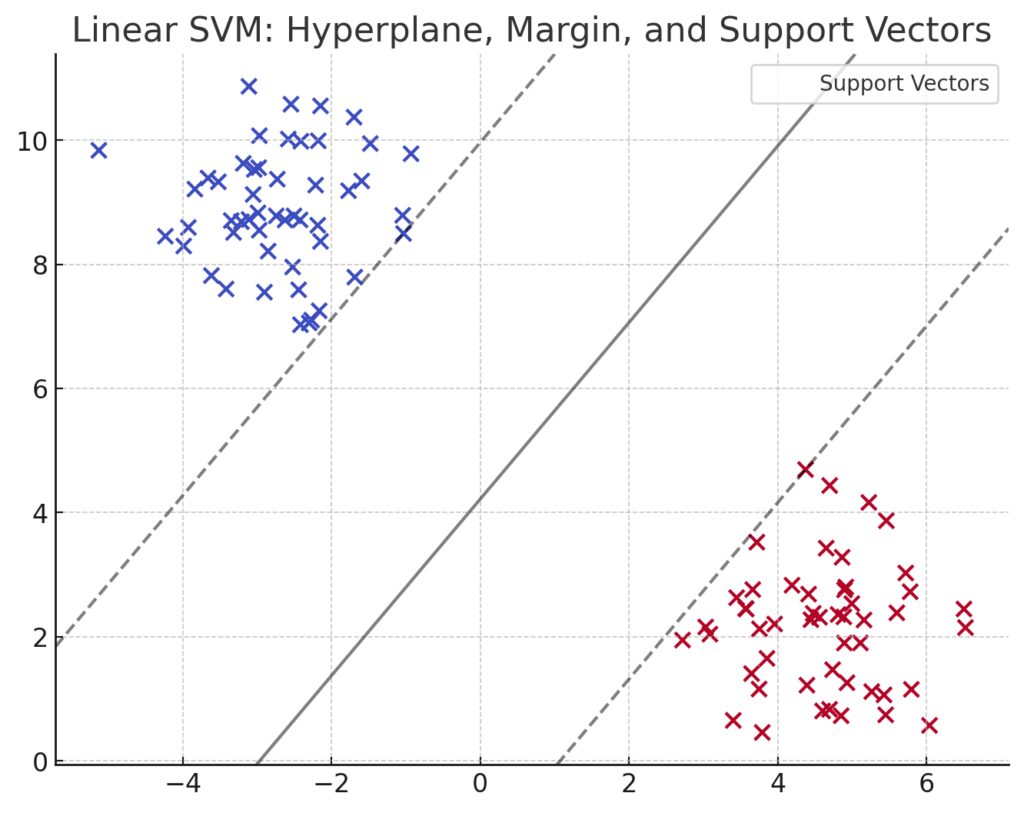
The goal of an SVM is simple: find the best boundary, or decision boundary, that separates classes in the data. This boundary, known as a hyperplane, divides the space in such a way that each class is on one side of the hyperplane.
At its core, SVMs strive to maximize the margin between data points of different classes, ensuring the model generalizes well to unseen data. In essence, it’s all about finding the line that best separates the categories of data.
How Do SVMs Work in Simple Terms?
Imagine you have two types of fruits—apples and oranges—and you need to draw a line (or a boundary) that separates them based on their features, like size and color. That’s essentially what an SVM does: it identifies the best line, or hyperplane, that divides the categories of data as clearly as possible.
SVM doesn’t just find any line, though. It tries to find the one that leaves the widest possible margin between the two groups. This margin is the distance between the hyperplane and the closest data points from each class, known as support vectors. SVM picks the line where this margin is largest, so it’s not just about separating the data but doing so in a way that maximizes the space between them, ensuring better generalization.
Key Concepts Behind SVMs: Hyperplanes and Support Vectors
To truly understand SVMs, you need to grasp two key concepts: hyperplanes and support vectors.

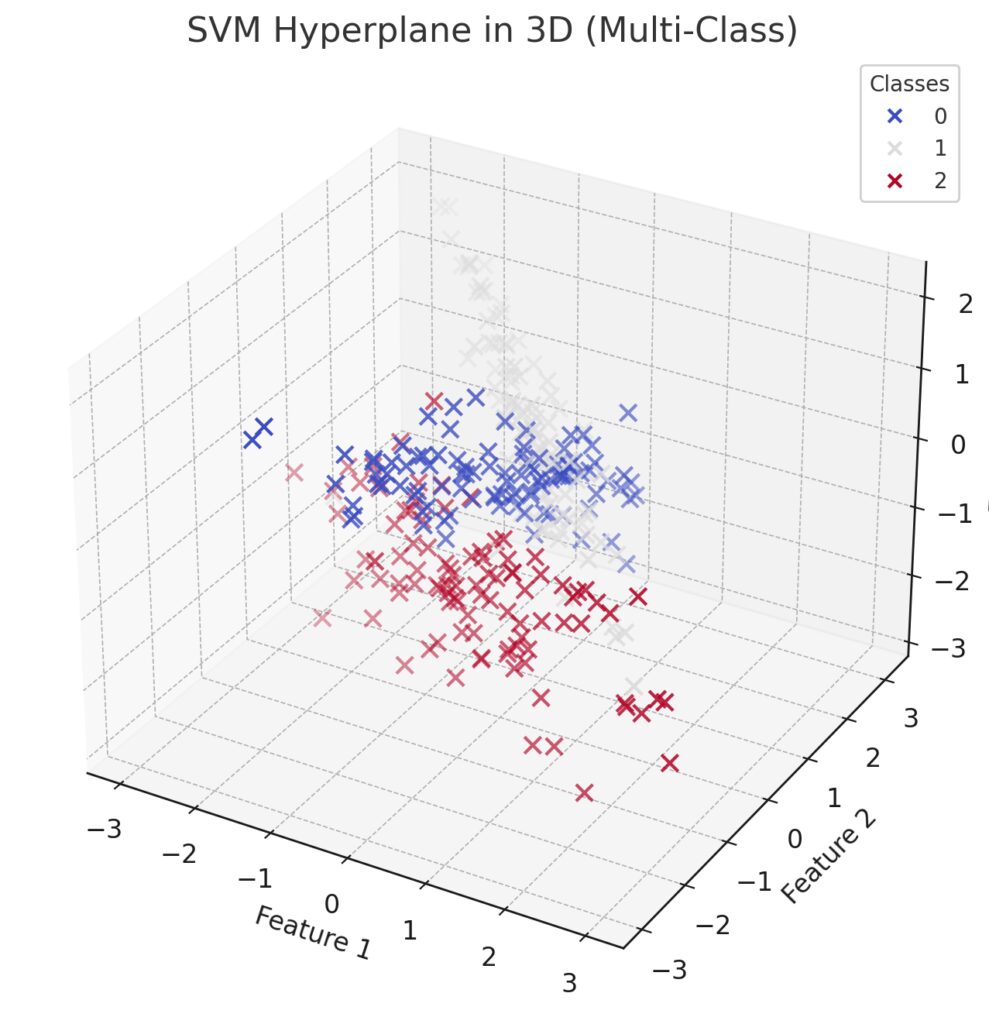
- Hyperplane: In two dimensions, this is a simple line. In higher dimensions, it’s a plane or space that separates different data classes. For a given dataset, SVM tries to find the hyperplane that separates the classes in the best possible way.
- Support Vectors: These are the data points that are closest to the hyperplane. They are critical because they define the margin of separation. The SVM algorithm focuses on these points to establish the optimal hyperplane. In fact, if you moved a support vector, the hyperplane would shift, affecting the entire classification boundary.
The support vectors are vital because they determine how the hyperplane is drawn. The further the support vectors are from the hyperplane, the wider the margin, and this is exactly what SVM aims to achieve.
Understanding the SVM Algorithm Step-by-Step
To break down how SVM works, let’s go step-by-step through the algorithm:
- Data Preparation: You start with a labeled dataset, where each data point belongs to one of two classes.
- Hyperplane Calculation: The SVM algorithm calculates the optimal hyperplane (a decision boundary) that best separates the two classes.
- Maximizing the Margin: The algorithm identifies the support vectors—data points that lie closest to the hyperplane—and adjusts the hyperplane to maximize the margin between these points.
- Classification: Once the hyperplane is established, any new data point can be classified by seeing which side of the hyperplane it falls on.
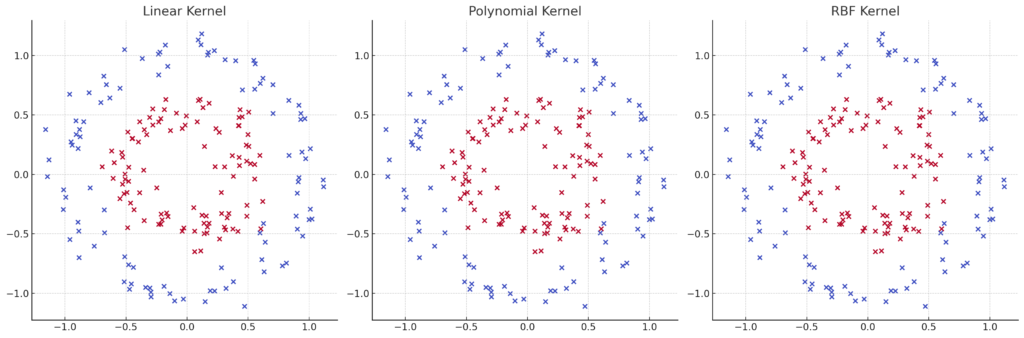
If the data isn’t linearly separable (meaning a straight line can’t divide the classes), SVM uses the kernel trick to transform the data into a higher-dimensional space, where a linear separation can be found.
The Power of SVMs in Classification and Regression
One of the reasons SVMs are so powerful is their versatility in both classification and regression tasks. Though they’re primarily known for binary classification, SVMs can also be extended for multi-class classification problems. This is done using techniques like one-vs-one or one-vs-all strategies, allowing SVMs to classify data into more than two categories.
In regression tasks (called SVR, or Support Vector Regression), SVMs aim to fit the best boundary that lies within a certain margin of the data. Instead of maximizing the margin between classes, SVR tries to minimize the prediction error while keeping data points within a specified tolerance.
SVMs excel at both classification and regression because of their ability to handle high-dimensional data and small sample sizes effectively, all while minimizing overfitting.
Why SVMs are Effective in High-Dimensional Spaces
SVMs shine in high-dimensional spaces, meaning they perform well even when the number of features (or dimensions) is greater than the number of data points. This makes them an excellent choice for applications like text classification, bioinformatics, and image recognition, where the data often has many dimensions.
The beauty of SVM lies in its ability to work with complex data structures, finding hyperplanes even in high-dimensional feature spaces. It avoids overfitting by focusing on the support vectors and ignoring the irrelevant data points that don’t contribute to the decision boundary.
Even when the data cannot be separated linearly, SVM can apply the kernel trick to project the data into a higher dimension, where a linear hyperplane can be drawn to separate the classes.
Linear vs. Nonlinear SVMs: What’s the Difference?
When working with Support Vector Machines (SVMs), you’ll encounter two types: linear SVMs and nonlinear SVMs. The choice between the two depends on whether your data can be separated by a straight line (in 2D) or a flat hyperplane (in higher dimensions).
Linear SVMs
A linear SVM is used when the data is linearly separable, meaning a straight line (or hyperplane in higher dimensions) can divide the data points into distinct classes. For example, if you’re trying to classify points on a plane, and you can draw a straight line to separate them perfectly, a linear SVM is your go-to model.
Linear SVMs are fast and computationally less expensive, making them ideal for:
- Simple datasets where classes are clearly separated.
- High-dimensional datasets like text classification, where data often behaves linearly in a transformed space (e.g., TF-IDF vectors).
Nonlinear SVMs
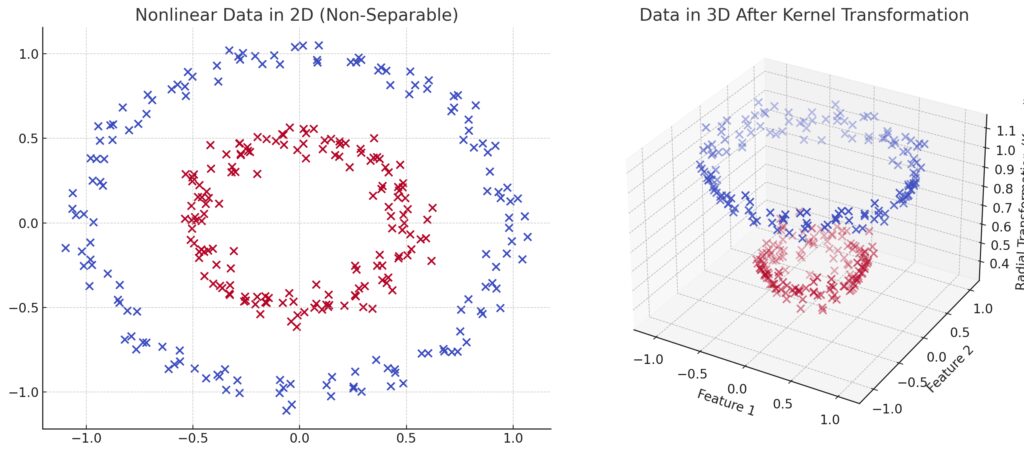
Not all data is neatly separable by a straight line. Enter nonlinear SVMs. When data points form complex shapes that a straight line can’t separate, a nonlinear SVM comes into play. Nonlinear SVMs work by mapping the data into a higher-dimensional space where it becomes easier to find a linear separator, even though the data is not linearly separable in its original form.
For example, imagine a dataset where points of different classes form concentric circles. A linear SVM wouldn’t be able to find a straight line to divide these points. But a nonlinear SVM can transform the data (using the kernel trick) so that a simple linear boundary can be drawn in a higher-dimensional space, where those circles become separable.
The Role of the Kernel Trick in SVMs
One of the most powerful aspects of SVMs is the kernel trick. This allows SVMs to handle nonlinear data by transforming it into a higher-dimensional space where it becomes linearly separable. But the beauty of the kernel trick is that it does this without explicitly computing the transformation—saving computation time and resources.

How the Kernel Trick Works
At its core, the kernel trick takes the original data, transforms it using a kernel function, and allows the SVM to find a linear separator in this new, transformed space. The transformation happens behind the scenes, so SVM can operate efficiently even in high-dimensional feature spaces.
There are several types of kernel functions commonly used:
- Linear Kernel: Used when data is linearly separable (i.e., a straight line can separate the classes).
- Polynomial Kernel: Maps the original data to a higher-dimensional space based on polynomial degrees. This allows SVMs to capture more complex relationships between data points.
- Radial Basis Function (RBF) Kernel: One of the most commonly used kernels. The RBF kernel is especially effective in handling data that isn’t linearly separable, by mapping it into a higher-dimensional space.
- Sigmoid Kernel: Often used in neural networks, it can also be applied in SVMs for nonlinear transformations.
Choosing the right kernel depends on the data and problem at hand. While the RBF kernel is often the default choice because of its flexibility, polynomial kernels may be more suitable when the relationship between data points follows a clear polynomial pattern.
Hyperparameters in SVMs: Regularization and the C Parameter
In any machine learning model, hyperparameters play a crucial role in balancing the model’s performance and its ability to generalize. SVMs have two critical hyperparameters you should be familiar with: C (regularization parameter) and γ (gamma) for kernel functions like RBF.
The C Parameter
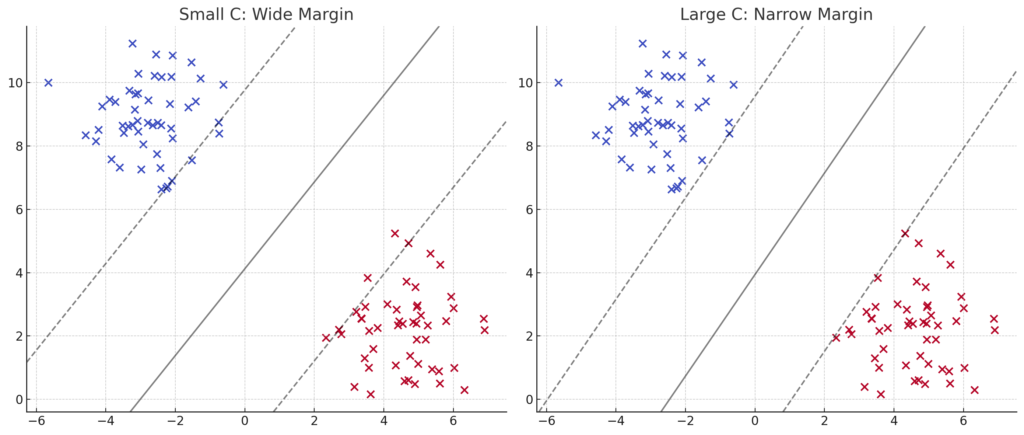
The C parameter controls the trade-off between maximizing the margin and minimizing classification errors. A small C creates a larger margin that ignores some data points (allowing misclassification), while a large C creates a smaller margin that classifies more points correctly but risks overfitting.
- High C: The model aims to classify every training data point correctly. However, this increases the risk of overfitting, as the hyperplane may become too sensitive to individual points, including outliers.
- Low C: The model allows some misclassification in exchange for a wider margin, making it more generalizable but potentially less accurate on training data.
Gamma (γ) Parameter
When using kernel functions like RBF or polynomial kernels, the gamma parameter becomes important. It defines how far the influence of a single training example reaches.
- Low gamma: Each point has a far-reaching influence, resulting in a smoother, simpler decision boundary.
- High gamma: Each point’s influence is more localized, meaning the decision boundary is highly sensitive to the training data, which can lead to overfitting.
Tuning these hyperparameters properly is crucial to ensuring your SVM model performs optimally on new, unseen data.
SVMs in Real-World Applications
Support Vector Machines have been successfully applied in a wide range of industries and tasks, particularly where classification is key. Here are some prominent real-world applications of SVMs:
- Text Classification: SVMs excel at categorizing documents and emails based on their content, such as spam detection or sentiment analysis. Due to their ability to handle high-dimensional data, SVMs are widely used for tasks like categorizing news articles or classifying customer reviews.
- Image Recognition: SVMs are often used to recognize objects or faces in images. They have been employed in facial recognition systems, handwriting digit recognition (like the MNIST dataset), and even medical imaging for identifying tumors in MRI scans.
- Bioinformatics: In genetics and bioinformatics, SVMs are used for classifying proteins, analyzing gene expression, and predicting disease outcomes based on large datasets with complex features.
- Financial Analysis: SVMs can help detect fraud, predict market trends, or classify credit risks in financial institutions. By identifying patterns in past transactions or customer behaviors, they can flag potentially fraudulent activity with high accuracy.
SVMs’ versatility and ability to handle complex, high-dimensional data make them an invaluable tool in machine learning applications where precision and accuracy are critical.
How to Tune SVMs for Better Performance
Like any machine learning model, SVMs require careful hyperparameter tuning to achieve optimal performance. Some key strategies include:
- Grid Search: One of the most popular methods for tuning SVM hyperparameters like C and gamma. Grid search explores a range of possible values for each parameter, helping you identify the combination that produces the best model.
- Cross-Validation: To ensure your SVM model generalizes well, use cross-validation during hyperparameter tuning. This involves splitting your data into training and validation sets to test how well the model performs on different data subsets.
- Scaling Features: SVMs are sensitive to the scale of the input data, so it’s essential to normalize or scale your features. Using techniques like min-max scaling or standardization helps the algorithm perform better, especially when using kernel functions.
- Kernel Selection: Experimenting with different kernel functions (linear, RBF, polynomial) and tweaking the gamma parameter can lead to significant performance improvements, especially in nonlinear classification tasks.
Tuning these aspects of SVM ensures a balanced trade-off between model complexity and generalization, ultimately improving prediction accuracy and robustness.

SVM vs. Other Machine Learning Algorithms: Pros and Cons
When choosing a machine learning model, it’s crucial to compare Support Vector Machines (SVMs) with other popular algorithms like decision trees, logistic regression, and neural networks. Each has its strengths and weaknesses, and understanding how SVMs stack up against these methods will help you determine when SVM is the best option.
Pros of SVMs:
- Effective in High-Dimensional Spaces: SVMs work exceptionally well when dealing with high-dimensional data, making them a solid choice for text classification, image recognition, and other tasks where feature space can be vast.
- Handles Nonlinear Data: Thanks to the kernel trick, SVMs can tackle problems where the data isn’t linearly separable. By transforming the data into higher dimensions, they can find linear boundaries that separate complex datasets.
- Robust to Overfitting: By maximizing the margin between the classes, SVMs avoid overfitting, especially when combined with regularization.
- Works Well with Smaller Datasets: SVMs are highly effective with smaller sample sizes, as they only focus on the support vectors, the critical data points that lie closest to the decision boundary.
Cons of SVMs:
- Computationally Intensive: Training an SVM can be slow, especially with large datasets. The complexity grows with the number of samples and features, making them less efficient for very large-scale problems.
- Hard to Interpret: While decision trees or logistic regression models offer straightforward interpretability, SVMs are considered black box models. It’s hard to interpret how the algorithm makes its decisions, especially when using non-linear kernels.
- Sensitive to Feature Scaling: SVMs require that the input features be scaled or normalized because they rely on distances between data points. If features have varying ranges, it can skew the results.
- Not Ideal for Noisy Data: SVMs can struggle with datasets that have overlapping classes or noisy data, which can lead to misclassification. Tuning the regularization parameter (C) can help, but this adds complexity.
Comparison with Other Algorithms:
- Logistic Regression: Both SVMs and logistic regression are used for binary classification, but SVMs generally perform better with complex, high-dimensional data, while logistic regression is simpler and easier to interpret.
- Decision Trees: Decision trees are fast and interpretable but prone to overfitting, especially on noisy datasets. SVMs, while slower to train, tend to generalize better and work well with small, complex datasets.
- Neural Networks: Neural networks, like SVMs, can handle non-linear relationships and high-dimensional data. However, they require more data and computational resources to train. SVMs are often preferred when data is limited or computation time is a concern.
Ultimately, SVMs are a great choice when you need high accuracy and are working with complex data, but other models may be more appropriate for simpler, less computationally demanding problems.
SVMs and Outliers: Why SVMs Handle Them Well
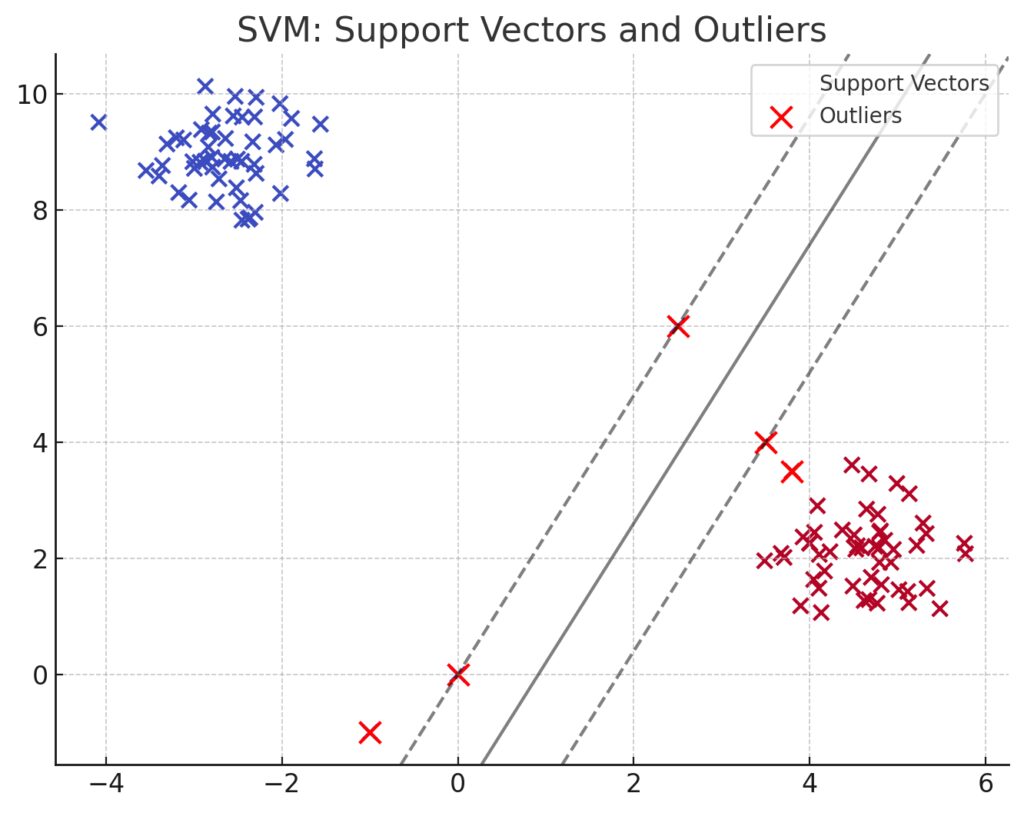
Outliers can wreak havoc on many machine learning models, leading to poor predictions and overfitting. Support Vector Machines (SVMs) are relatively robust to outliers because of the way they prioritize support vectors, which are the key data points that define the margin around the decision boundary.
How SVMs Deal with Outliers:
- Focus on Support Vectors: SVMs mainly focus on the data points closest to the decision boundary (support vectors), while ignoring most of the data points that are further away. Outliers that are far from this boundary don’t impact the model as much, reducing the risk of distortion in predictions.
- Regularization with the C Parameter: The C parameter in SVM allows you to control the trade-off between maximizing the margin and minimizing classification error. When you increase C, the model tries to classify more points correctly, including outliers, but at the risk of overfitting. Decreasing C allows the model to ignore outliers, creating a more generalizable model with a wider margin.
However, if your dataset contains a large number of outliers, SVM may struggle. In such cases, data preprocessing steps like outlier detection and removal should be considered before training the model.

Common Challenges and Pitfalls When Using SVMs
While SVMs are powerful, they are not immune to challenges. Knowing the common pitfalls will help you avoid issues and get the most out of this algorithm.
1. Feature Scaling
One of the biggest pitfalls when using SVMs is failing to scale the input features. SVMs depend on distance measures (like Euclidean distance), so if features have vastly different scales (e.g., age vs. income), it will distort the decision boundary. Normalizing or standardizing your data before applying SVM is essential for accurate results.
2. Kernel Selection
Choosing the wrong kernel can lead to poor performance. While the RBF kernel is a versatile default, some datasets may work better with polynomial or even linear kernels. It’s important to experiment with different kernel functions and tune their hyperparameters (like gamma for RBF) to find the best fit for your data.
3. Overfitting with High C
If you set the C parameter too high, the SVM model will focus on classifying every training point correctly, which can result in overfitting. This means that while the model performs well on the training data, it may fail to generalize to unseen data. A lower C allows for a wider margin and helps the model generalize better, even if it misclassifies some training points.
4. Computational Intensity
SVMs can become computationally expensive, especially when using nonlinear kernels on large datasets. Training times can be long, and memory consumption can be high. In such cases, alternatives like stochastic gradient descent (SGD) or using an approximate SVM may be more efficient for large-scale problems.
5. Handling Imbalanced Data
SVMs can struggle with imbalanced datasets, where one class significantly outnumbers the other. In such cases, the decision boundary can be skewed toward the majority class, leading to poor classification of the minority class. Techniques like oversampling, undersampling, or adjusting the class weights in the SVM model can help address this issue.
Tools and Libraries for Implementing SVMs
If you’re ready to implement SVMs, several libraries and tools make the process easier, especially in Python.
- Scikit-learn (Python)
Scikit-learn is one of the most popular libraries for machine learning in Python and offers easy-to-use functions for implementing SVMs. TheSVCclass in Scikit-learn provides a high-level interface for training SVM classifiers, whileSVRsupports regression tasks.- Documentation: Scikit-learn SVM
- LIBSVM
LIBSVM is a widely-used library that supports SVM for classification, regression, and distribution estimation. It’s available in multiple languages, including Python, R, and Java.- Website: LIBSVM
- TensorFlow
While more complex, TensorFlow offers deep learning functionalities and can integrate SVM algorithms. If you’re building a large machine learning pipeline or need to incorporate deep learning with SVM, TensorFlow offers the flexibility you need.- Documentation: TensorFlow
- PyTorch
Like TensorFlow, PyTorch is a deep learning library, but it’s more suitable for developers who want dynamic computation graphs. PyTorch can also be used for custom SVM implementations, particularly for integrating with neural networks.- Documentation: PyTorch
- Weka (Java)
Weka is a popular Java-based platform for machine learning. It has a built-in SVM implementation that allows you to experiment with various kernels, hyperparameters, and pre-processing techniques via a user-friendly interface.- Website: Weka
When to Choose SVMs Over Other Algorithms
Knowing when to choose SVMs over other algorithms can be crucial for achieving the best results in your machine learning tasks. Here’s when SVMs are the best choice:
- High-dimensional Data: SVMs are particularly effective for high-dimensional feature spaces, such as text classification or genomics. If your dataset contains many features, SVMs are likely to perform better than models like decision trees or logistic regression.
- Small or Medium-Sized Datasets: SVMs perform well on smaller datasets, where neural networks may overfit due to a lack of data. SVMs focus on maximizing the margin between the closest data points, making them robust even with limited training data.
- Complex Boundaries: If your data isn’t linearly separable and requires more complex boundaries, SVMs with the kernel trick can find a decision boundary that other algorithms like logistic regression or decision trees might miss.
- Classification Tasks: SVMs are particularly powerful for binary classification problems, such as email spam detection, image recognition, or fraud detection.
While SVMs are versatile, other algorithms like neural networks may be better suited for problems with large amounts of data or complex patterns. But when precision and handling of high-dimensional or non-linear data are critical, SVMs are a go-to solution.
The Future of SVMs in Machine Learning
As machine learning continues to evolve, Support Vector Machines (SVMs) remain a reliable and robust algorithm. However, with the rise of deep learning and more sophisticated models, some wonder where SVMs fit in the broader machine learning landscape. Let’s explore where SVMs are headed and how they may continue to play an important role in the future of AI.
SVMs in Hybrid Models
One exciting area for SVMs in the future is their potential integration with neural networks and other advanced machine learning models. Hybrid models combine the strengths of different algorithms to improve overall performance. For example, combining SVMs with convolutional neural networks (CNNs) for image recognition or recurrent neural networks (RNNs) for sequence-based data can yield powerful, robust models.
SVMs offer several benefits when used alongside deep learning models:
- Faster convergence: By using SVMs to classify data or handle lower-dimensional tasks, the computational burden on deep learning models can be reduced.
- Better feature engineering: SVMs can extract high-quality features from complex data and feed these into neural networks, improving overall accuracy.
Incorporating SVMs into hybrid models can offer enhanced performance and better interpretability compared to using deep learning models alone, especially in cases with limited data.
SVMs in Streaming and Real-Time Data Processing
With the increasing need for real-time decision-making in areas like self-driving cars, financial trading, and IoT devices, machine learning models need to process data in real-time. While traditional SVMs can be computationally heavy, advances in online learning techniques are making SVMs more adaptable to real-time environments.
Online SVMs allow for dynamic updating of the model as new data arrives, which is crucial in fast-changing domains. This enables the model to make predictions without retraining from scratch, making SVMs more suitable for streaming data and dynamic environments.
SVMs and Quantum Computing
As quantum computing becomes more of a reality, SVMs could see a resurgence in popularity. Quantum algorithms have the potential to perform calculations exponentially faster than traditional computers, and SVMs, with their reliance on matrix operations and optimization techniques, are well-suited for this kind of acceleration.
Quantum Support Vector Machines (QSVM) have already been a focus of research, where quantum computers solve the optimization problem involved in training an SVM much faster than classical machines. This could allow SVMs to handle larger datasets and higher-dimensional spaces much more efficiently, expanding their practical applications.
SVMs in Explainable AI (XAI)
As machine learning models become more powerful, the demand for explainability has increased, especially in sensitive areas like healthcare, finance, and criminal justice. SVMs offer a level of interpretability that complex models like deep neural networks often lack.
While SVMs are sometimes referred to as black box models, particularly when using nonlinear kernels, they are still more interpretable than deep learning models. For example:
- Linear SVMs allow us to directly see which features are most important in making a classification.
- Support vectors provide insights into which data points are critical for defining the decision boundary.
With the push for more transparent AI models, SVMs might find new use cases in industries where understanding how decisions are made is as important as the decisions themselves.
SVMs and Big Data
One area where SVMs have faced challenges is in handling massive datasets due to the computational cost of training. However, advancements in parallel computing and distributed machine learning may offer solutions for this. Libraries like Apache Spark and frameworks like Hadoop allow for distributed training of machine learning models, including SVMs, making it easier to scale SVMs to big data problems.
Additionally, algorithms such as Stochastic Gradient Descent (SGD) and Dual Coordinate Descent have been developed to optimize SVMs for large-scale data. These methods speed up training by focusing on a subset of data or features at a time, enabling SVMs to handle data sizes that were once considered impractical.
With these improvements, SVMs could continue to be a relevant and effective tool even in the era of big data.
Conclusion: SVMs in the Machine Learning Ecosystem
Despite the surge in popularity of deep learning and other complex algorithms, Support Vector Machines (SVMs) hold their ground as a powerful, adaptable, and effective tool in the machine learning toolbox. Their ability to handle high-dimensional data, nonlinear relationships, and small datasets makes them particularly valuable in specific domains such as text classification, image recognition, and bioinformatics.
While SVMs may not be the default choice for every machine learning problem—particularly those involving massive amounts of data—new advancements, such as quantum computing and hybrid models, suggest that they will remain an important part of the future of AI.
As explainability and real-time processing become more critical in AI systems, SVMs’ balance of simplicity, effectiveness, and versatility will ensure they continue to be a relevant option for machine learning practitioners across many industries.