
Implementing a simple perceptron in C with the delta rule for error correction can be a rewarding way to grasp fundamental machine learning concepts and to understand the nuts and bolts of how neural networks learn.
In this guide, we’ll walk you through implementing the delta rule, a key ingredient in updating the weights of a perceptron based on the error observed.
We’ll start with a brief overview of perceptrons and the delta rule, and then dive into coding the perceptron in C.
Understanding the Perceptron and the Delta Rule
What is a Perceptron?
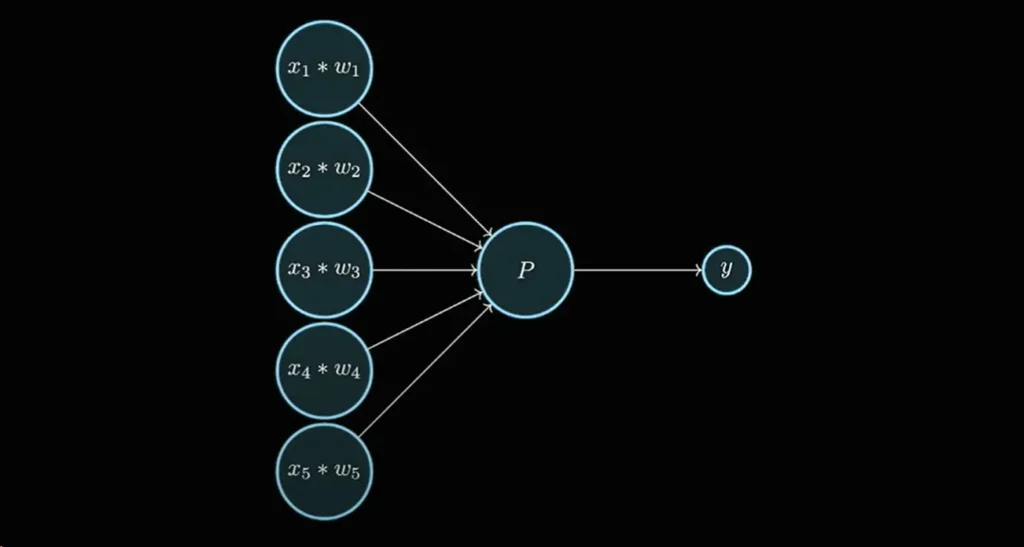
A perceptron is one of the simplest types of artificial neurons. It receives multiple inputs, applies weights to them, adds up the results, and then passes this through an activation function to produce an output. If the output is incorrect, the perceptron adjusts its weights to reduce the error. Over multiple iterations, this process helps the perceptron “learn.”
The Delta Rule
The delta rule (or the learning rule) is used to minimize the error by adjusting the weights of the perceptron. The weight adjustment formula for the delta rule is as follows:

This formula adjusts each weight slightly in the direction that reduces the error for each input example.
Setting Up the Perceptron Code in C
Let’s get into the code. We’ll implement a perceptron to solve a simple binary classification problem, where inputs are classified as either 0 or 1.
Step 1: Define Constants and Structure
First, define key constants and the structure to represent the perceptron.
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define LEARNING_RATE 0.1
#define EPOCHS 1000
typedef struct {
float *weights;
int num_inputs;
} Perceptron;
This code defines:
- A constant
LEARNING_RATEfor the delta rule. - A constant
EPOCHSto control the number of training cycles. - A
Perceptronstructure with an array of weights and a count of inputs.
Step 2: Initialize the Perceptron
Initialize the perceptron by allocating memory for weights and setting them to small random values.
void initialize_perceptron(Perceptron *p, int num_inputs) {
p->num_inputs = num_inputs;
p->weights = (float *)malloc((num_inputs + 1) * sizeof(float)); // +1 for bias
// Initialize weights to small random values
for (int i = 0; i <= num_inputs; i++) {
p->weights[i] = (float)rand() / RAND_MAX - 0.5;
}
}
This function sets each weight (including the bias weight) to a random value between -0.5 and 0.5.
Step 3: Activation Function
Define the perceptron’s activation function, here using a step function.
int activation_function(float sum) {
return sum >= 0 ? 1 : 0;
}
This function returns 1 if the sum is greater than or equal to zero, and 0 otherwise.
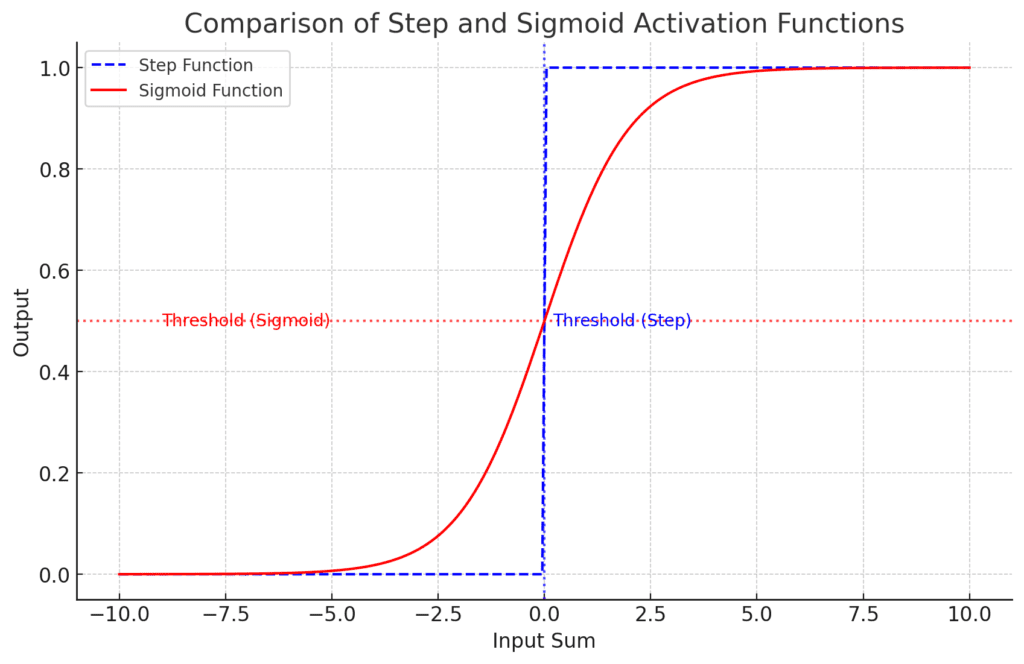
Step Function: Shown as a dashed line, it abruptly changes from 0 to 1 at the threshold (input sum of 0).
Sigmoid Function: A smooth curve, ranging between 0 and 1, with a threshold crossing at an output of 0.5.
This plot highlights the difference between the discrete step response and the continuous sigmoid response, which is more gradual around the threshold.
Step 4: Predict Function
Create a function to calculate the perceptron’s output given an input.
int predict(Perceptron *p, float *inputs) {
float sum = p->weights[0]; // bias weight
for (int i = 0; i < p->num_inputs; i++) {
sum += inputs[i] * p->weights[i + 1];
}
return activation_function(sum);
}
This function computes the weighted sum of inputs and applies the activation function to return the perceptron’s output.
Step 5: Training with the Delta Rule
Implement the delta rule to train the perceptron. For each input, calculate the error and adjust the weights accordingly.
void train(Perceptron *p, float inputs[][2], int targets[], int num_samples) {
for (int epoch = 0; epoch < EPOCHS; epoch++) {
for (int i = 0; i < num_samples; i++) {
int prediction = predict(p, inputs[i]);
int error = targets[i] - prediction;
// Update bias weight
p->weights[0] += LEARNING_RATE * error;
// Update weights for inputs
for (int j = 0; j < p->num_inputs; j++) {
p->weights[j + 1] += LEARNING_RATE * error * inputs[i][j];
}
}
}
}
This function iterates over the samples for a fixed number of EPOCHS. It calculates the error as the difference between the target and predicted values and then applies the delta rule to update weights.

Activation: Determines output from net input.
Error Calculation: Measures the prediction error.
Weight Update: Adjusts weights to minimize the error in future iterations.
This table provides a concise overview of the perceptron learning steps using the delta rule, with each formula facilitating a deeper understanding of the process. Let me know if you need any more details or modifications!
Step 6: Testing the Perceptron
After training, test the perceptron to see if it learned to classify correctly.
void test_perceptron(Perceptron *p, float inputs[][2], int targets[], int num_samples) {
for (int i = 0; i < num_samples; i++) {
int output = predict(p, inputs[i]);
printf("Input: [%f, %f] Predicted: %d, Target: %d\n", inputs[i][0], inputs[i][1], output, targets[i]);
}
}
This function takes an array of inputs and expected outputs, displays the perceptron’s predictions and the target labels, allowing us to evaluate accuracy visually.
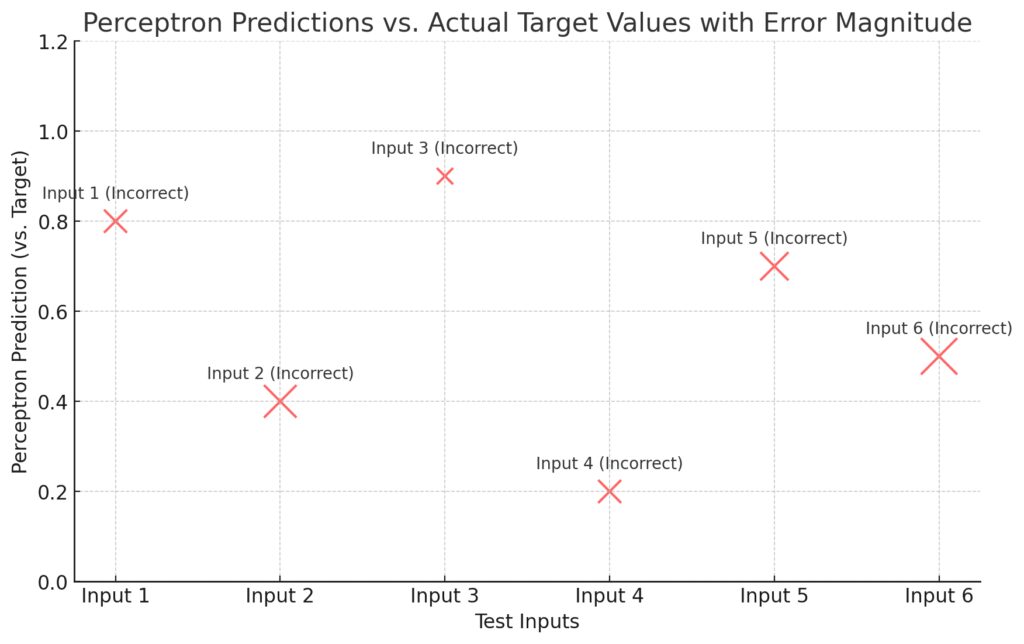
Bubbles: Each represents a test input, with size indicating the magnitude of error (larger bubbles show greater error).
Color Coding:Green: Correctly classified by the perceptron.
Red: Incorrectly classified.
Labels: Each bubble is labeled with the test input name and whether it was classified correctly or incorrectly.
This visualization helps identify the accuracy of the perceptron’s predictions and highlight cases with significant classification errors
Step 7: Main Function to Tie It All Together
In main(), define training samples, initialize the perceptron, train it, and then test its accuracy.
int main() {
// Define training data for an OR gate
float inputs[4][2] = { {0, 0}, {0, 1}, {1, 0}, {1, 1} };
int targets[4] = { 0, 1, 1, 1 };
Perceptron p;
initialize_perceptron(&p, 2);
// Train the perceptron
train(&p, inputs, targets, 4);
// Test the perceptron
printf("Testing Perceptron:\n");
test_perceptron(&p, inputs, targets, 4);
// Clean up
free(p.weights);
return 0;
}
This example is based on an OR gate, where the output should be 1 if either of the inputs is 1, and 0 only if both inputs are 0. You could easily modify the inputs and targets for other binary functions, such as AND or NAND.
Compiling and Running the Code
To compile and run the perceptron in a C environment, use the following command:
gcc perceptron.c -o perceptron -lm
./perceptron
This should display the output, showing the perceptron’s predicted results and the actual targets, allowing you to observe how well the perceptron learned.
Key Takeaways
By following this tutorial, you’ve built a basic perceptron in C with the delta rule for training. Here are some important points:
- The delta rule is foundational for error correction in perceptrons.
- Learning rate influences the step size for weight adjustments.
- Epochs control how many times the model sees the training data.
This implementation demonstrates the core principles of neural networks, serving as a stepping stone to more complex architectures.
FAQs
How do I initialize weights in the perceptron?
Weights in a perceptron are usually initialized to small random values to ensure that the learning process starts from a neutral point. This randomness helps the network avoid symmetry, enabling each weight to contribute differently to the prediction. In C, you can use rand() to generate small random numbers and scale them to a range like -0.5 to 0.5.
Why do we need an activation function?
The activation function in a perceptron determines whether the neuron “fires” or not. In a binary classification problem, for example, a step function is often used as the activation function, outputting 1 if the weighted sum of inputs exceeds a threshold and 0 otherwise. This function is essential as it converts the continuous sum of weighted inputs into a discrete class prediction.
What are common values for the learning rate?
The learning rate (η) controls the size of each weight adjustment. Typical values range from 0.01 to 0.1 for most applications. A smaller learning rate results in slower, more gradual learning, which can help prevent overshooting the optimal solution. Larger values, though faster, can lead to unstable training and may cause the perceptron to oscillate without finding the best weights.
How many epochs should I use?
The number of epochs (full passes through the training data) needed depends on the complexity of the problem and the chosen learning rate. For basic binary classification tasks, 500 to 1000 epochs is usually sufficient. However, if the perceptron struggles to converge, try increasing the epochs or reducing the learning rate for more controlled learning.
Can a single-layer perceptron solve non-linear problems?
No, a single-layer perceptron cannot solve non-linear problems like XOR (exclusive OR). Perceptrons are limited to linearly separable problems, where a single line (or hyperplane in higher dimensions) can separate the classes. For non-linear problems, multilayer perceptrons with additional layers and non-linear activation functions are required.
How do I implement the delta rule for training in C?
The delta rule can be implemented in C by calculating the error for each training example and adjusting the weights based on the error. In a loop, go through each sample, compute the prediction, calculate the error as (target - prediction), and update the weights using the delta rule formula. Running this adjustment multiple times over the data (epochs) allows the perceptron to improve.
What are common challenges when training a perceptron in C?
Common challenges include overflow issues with large inputs or weights, slow convergence due to poor learning rate choices, and difficulty handling non-linearly separable data. Additionally, debugging can be complex if the output isn’t as expected, especially since C lacks built-in libraries for neural networks, so all matrix and vector operations must be coded manually.
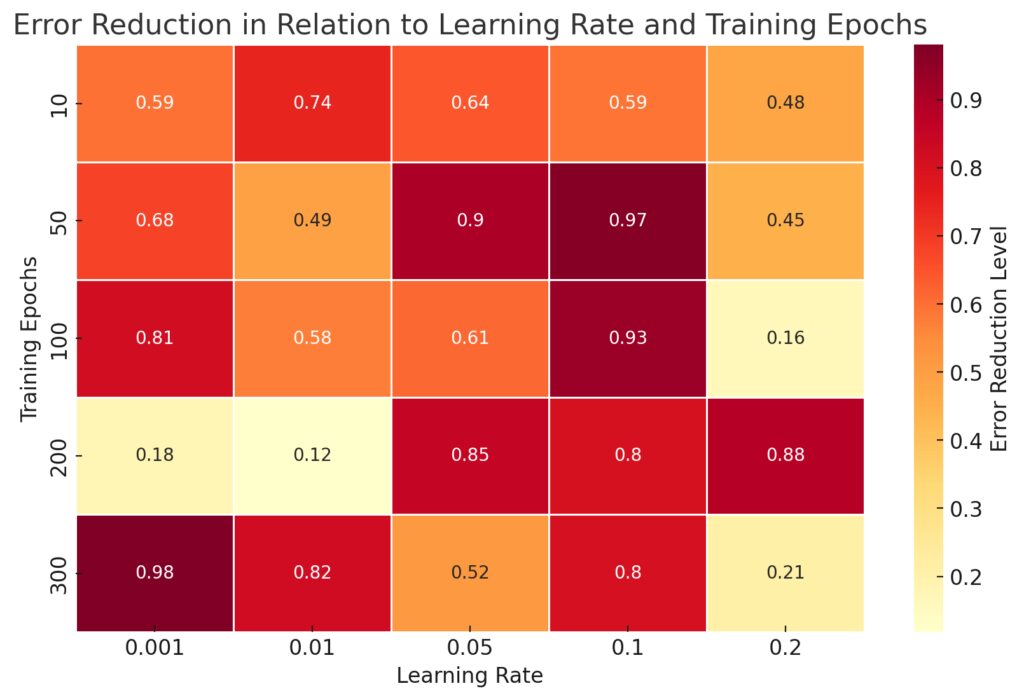
X-axis: Learning rates.
Y-axis: Number of training epochs.
Color Gradient: Indicates levels of error reduction, with darker shades representing more effective reduction.
This visualization helps highlight optimal combinations of learning rate and epochs for achieving convergence with minimal error.
How can I test if my perceptron is learning?
To test if your perceptron is learning, evaluate its predictions on the training data after each epoch. Check if the error (difference between prediction and target output) decreases over time. If the perceptron learns correctly, it should begin to classify inputs with increasing accuracy as epochs progress. You can visualize the training accuracy or track the cumulative error to monitor learning.
Are there any C libraries for implementing neural networks?
Although C does not have as many libraries for machine learning as Python, some libraries like FANN (Fast Artificial Neural Network Library) or tiny-dnn can assist with implementing neural networks. However, for educational purposes, building a perceptron from scratch can provide valuable insights into the workings of neural networks.
How do I handle multiple input features in a perceptron?
A perceptron can handle multiple input features by assigning a weight to each one. In your code, represent these weights as an array, where each index corresponds to a feature. The perceptron calculates the weighted sum of all features and applies the activation function to determine the output. When training, each weight is updated according to the delta rule based on its corresponding input feature.
For example, if your perceptron has two input features x1x_1x1 and x2x_2x2, then the weighted sum zzz would be:
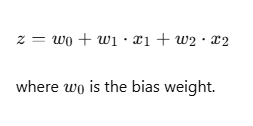
Why is a bias weight added to the perceptron?
A bias weight w0w_0w0 is added to the perceptron to allow it to classify data that is not centered around the origin. Without a bias, the perceptron’s decision boundary would be forced to pass through the origin, which limits its flexibility. The bias term allows the perceptron to shift the decision boundary up or down, making it more adaptable for a variety of data distributions.
In code, you handle the bias by initializing it as part of the weight array and always setting its input to 1. This way, during each calculation, the bias weight adds a constant offset to the sum of weighted inputs.
How does the perceptron handle categorical data?
The perceptron itself only handles numerical input. If you have categorical data (e.g., “Red”, “Blue”, “Green”), you’ll need to convert it into a numerical format before passing it to the perceptron. Common approaches include:
- One-hot encoding: Represent each category as a binary vector where only one element is 1, and the rest are 0.
- Integer encoding: Assign an integer value to each category (e.g., Red = 1, Blue = 2), though this method can introduce unintended ordering.
Once encoded, each category can be treated as an input feature with its own weight, allowing the perceptron to learn associations with different categories.
What should I do if my perceptron isn’t learning correctly?
If your perceptron isn’t learning or fails to classify inputs accurately, try the following adjustments:
- Decrease the learning rate if the model oscillates or diverges.
- Increase the number of epochs to give the perceptron more time to adjust.
- Check the input scaling: Large values can lead to instability, so normalize or scale inputs to a smaller range.
- Inspect the initial weights: Although random initialization is usually sufficient, sometimes tweaking the range of initial weights can help.
Lastly, if your data isn’t linearly separable, the perceptron won’t learn correctly due to its limitations with such data. For complex problems, consider using a multilayer neural network.
How does the delta rule compare to backpropagation?
The delta rule is a simplified form of gradient descent that applies only to single-layer perceptrons. In contrast, backpropagation is a more sophisticated algorithm used for multilayer networks (or multilayer perceptrons). Backpropagation computes the error at each layer and propagates it backward through the network, updating weights at each layer.
While the delta rule minimizes error directly in a single-layer perceptron, backpropagation allows deeper networks to learn complex patterns by systematically adjusting weights at all layers.
Can I use a different activation function in a perceptron?
Yes, you can use other activation functions, though the classic perceptron uses a step function. Alternative activation functions include:
- Sigmoid function: Outputs a value between 0 and 1, suitable for probability-based predictions.
- ReLU (Rectified Linear Unit): Outputs zero for negative inputs and the input value itself for positive inputs.
These alternatives are often used in more complex neural networks, as they introduce non-linearity, allowing the network to model more complex patterns. However, single-layer perceptrons remain limited to linearly separable problems, even with different activation functions.
Why do perceptrons struggle with the XOR problem?
The XOR problem is the classic example of a non-linearly separable problem. In XOR, the input-output pairs cannot be separated by a single line (or plane). Since the perceptron can only create linear decision boundaries, it cannot correctly classify XOR inputs. To solve XOR, you would need at least one hidden layer with multiple neurons, enabling the model to learn a non-linear boundary.
This limitation of the perceptron led to the development of multilayer neural networks, where multiple layers can approximate complex, non-linear decision boundaries.
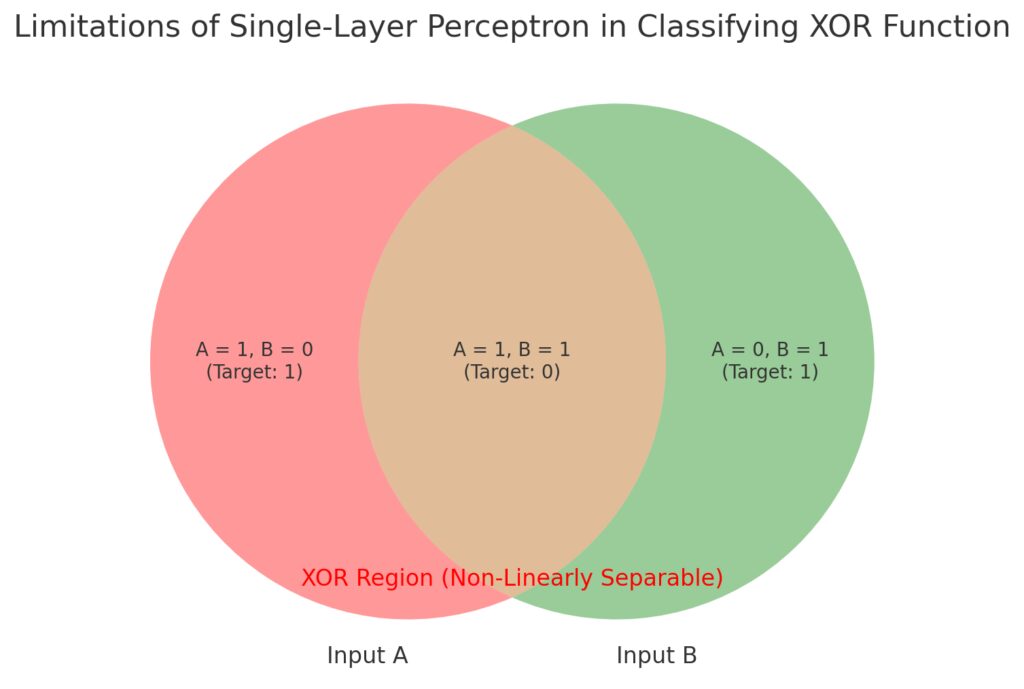
This illustration emphasizes why XOR classification requires more complex models (like multi-layer perceptrons).
How do I avoid overfitting in a perceptron?
Overfitting occurs when a model learns the training data too well, including noise, which reduces its ability to generalize to new data. In perceptrons, overfitting is less common due to the model’s simplicity, but it can still happen if the data is very limited or noisy. To minimize overfitting:
- Increase the amount of training data if possible.
- Add a small amount of regularization, such as weight decay, which discourages large weights.
- Reduce the number of epochs if the model starts to fit the training data too closely without improving general performance.
Overfitting is generally more problematic in complex neural networks, where multiple layers and many parameters can more easily memorize training data patterns.
What’s the difference between a perceptron and logistic regression?
Both perceptrons and logistic regression models are linear classifiers, but they differ in their approach:
- A perceptron uses a step activation function to produce discrete outputs (e.g., 0 or 1).
- Logistic regression uses the sigmoid function to produce a probability between 0 and 1, making it suitable for binary classification with probabilistic interpretation.
Moreover, logistic regression minimizes a cost function using gradient descent, whereas the perceptron uses the delta rule for discrete error correction. Logistic regression generally converges more smoothly and is commonly used when probabilistic output is required.
Can I apply the perceptron model to multi-class classification?
The single-layer perceptron is inherently a binary classifier, but it can be extended for multi-class classification using a technique called one-vs-all (OvA) or one-vs-one (OvO) classification:
- One-vs-All: Train a separate perceptron for each class, treating it as a binary classifier. Each perceptron determines if an input belongs to its class or not.
- One-vs-One: Train separate perceptrons for each pair of classes, choosing the final class based on which one wins the most classifications.
For true multi-class classification, multilayer neural networks are better suited, as they can inherently learn to differentiate between multiple classes through their more complex architectures.
Resources for Training a Perceptron in C and Understanding the Delta Rule
Online Courses and Tutorials
- Coursera – Neural Networks and Deep Learning by Andrew Ng
- A popular introductory course that covers the basics of neural networks, activation functions, and the learning rule. Although it uses Python, the concepts are transferable to C.
- Link: Coursera Neural Networks and Deep Learning
- edX – Fundamentals of Artificial Intelligence by Microsoft
- This course provides a broader introduction to AI and machine learning with modules on neural networks and supervised learning, including perceptrons.
- Link: edX Fundamentals of Artificial Intelligence
- TutorialsPoint – Perceptron Learning Algorithm
- A concise guide on the perceptron learning algorithm, including code examples and explanations that you can adapt for implementation in C.
- Link: TutorialsPoint Perceptron Learning Algorithm
Research Papers and Articles
- “An Introduction to Computing with Neural Nets” by Rojas (1996)
- This paper is a classic introductory text on neural networks and the mathematics behind them, including the perceptron and delta rule.
- Link: Available on Semantic Scholar
- “A Simplified Perceptron Learning Rule” by Rosenblatt (1958)
- The original research paper by Frank Rosenblatt introducing the perceptron. This is a foundational read for understanding the origins of the perceptron model.
- Link: Available in most academic databases like JSTOR or ResearchGate
C Programming Resources
- “The C Programming Language” by Brian Kernighan and Dennis Ritchie
- A comprehensive and timeless reference for learning C programming from the ground up, useful for understanding pointers, arrays, and memory management essential in perceptron implementation.
- Where to find: Amazon
- Tutorials and Guides on GeeksforGeeks
- GeeksforGeeks offers various tutorials on C programming, covering memory allocation, arrays, and pointers, which are crucial for neural network implementation.
- Link: GeeksforGeeks C Programming
- C Programming for Embedded Systems by Kirk Zurell
- While this book is about embedded systems, it provides practical insights into implementing efficient algorithms in C, making it useful for low-level programming and neural network implementation.
- Where to find: Amazon or Safari Books Online
Open-Source Libraries and Code Repositories
- FANN (Fast Artificial Neural Network Library)
- FANN is a C library that provides a flexible and efficient framework for building neural networks, including perceptrons. You can use it to explore neural network concepts in C and save time on boilerplate code.
- Link: FANN Library GitHub
- tiny-dnn
- A lightweight, header-only neural network library written in C++. Though primarily in C++, tiny-dnn is compatible with C, making it a good option for learning neural network concepts in lower-level languages.
- Link: tiny-dnn GitHub
- OpenAI Gym (for Understanding Concepts)
- Though primarily in Python, OpenAI Gym provides a variety of environments for testing machine learning algorithms. You could use it as a conceptual aid while implementing similar tasks in C.
- Link: OpenAI Gym
Practical Tools and Simulations
- Google Colab
- Google Colab is a free Jupyter notebook environment that runs in the cloud. While it doesn’t support C natively, you can use it to prototype algorithms in Python and then translate them to C for implementation.
- Link: Google Colab
- MATLAB and Simulink for Neural Networks
- MATLAB offers extensive toolboxes for neural network design and simulation, including single-layer perceptrons. These tools allow you to visualize weight changes and test perceptron algorithms before coding them in C.
- Link: MATLAB Neural Network Toolbox
- Visual Studio Code (with C/C++ extensions)
- Visual Studio Code is an excellent IDE for C programming. With its C/C++ extension, you can debug, compile, and test your perceptron implementation.
- Link: Visual Studio Code