Why Gradient Boosting Outperforms Random Forests

Gradient Boosting Machines (GBMs) have become a powerhouse in the world of machine learning due to their ability to produce highly accurate models.

While Random Forests have long been a go-to method for many data scientists due to their simplicity and robustness, Gradient Boosting Machines (GBMs) are rapidly gaining favor for their superior performance in numerous applications. But what exactly makes GBMs stand out?

Let’s dive into the fascinating world of gradient boosting and discover why it often outperforms other ensemble methods.

What is Gradient Boosting?

Gradient Boosting is a powerful ensemble technique that builds models sequentially, with each new model attempting to correct the errors made by the previous ones. Unlike Random Forests, which build all trees independently, GBMs create a sequence of models that each focuses on the mistakes of its predecessor. This iterative process allows GBMs to refine predictions and significantly improve accuracy.

The Mechanics of Gradient Boosting Machines

At the heart of a Gradient Boosting Machine lies the concept of minimizing loss through gradient descent. Essentially, each tree in a GBM is trained to predict the residuals—the difference between the actual values and the model’s predictions—from the previous tree. This correction process continues until the model reaches the desired level of accuracy.

In contrast, Random Forests create multiple decision trees independently and aggregate their results through majority voting (in classification) or averaging (in regression). While effective, this method can sometimes lack the precision that GBMs offer.

Why GBMs Often Outperform Random Forests

Gradient Boosting Machines often outperform Random Forests due to their ability to reduce both bias and variance. By focusing on the errors made by previous models, GBMs can fine-tune predictions more effectively. This iterative approach allows for greater accuracy, especially in complex datasets where patterns are not immediately obvious.

Furthermore, GBMs provide more control over model tuning. Through hyperparameters like learning rate, number of trees, and tree depth, you can carefully optimize the model to achieve the best performance for your specific task. This fine-tuning capability often leads to better results compared to the more rigid structure of Random Forests.

Applications Where GBMs Shine

Gradient Boosting Machines have proven their worth in various fields, particularly in finance, healthcare, and marketing. In finance, GBMs are used for credit scoring, fraud detection, and algorithmic trading, where accuracy is paramount. In healthcare, they help in disease prediction, patient risk scoring, and personalized medicine. Marketing teams leverage GBMs for customer segmentation, recommendation systems, and churn prediction.

The ability of GBMs to handle mixed data types and accommodate missing values makes them exceptionally versatile. They are particularly effective in scenarios where the dataset is highly imbalanced or contains numerous outliers.

Limitations of Gradient Boosting Machines

Despite their advantages, Gradient Boosting Machines are not without drawbacks. One of the primary concerns is their computational intensity. Training a GBM can be time-consuming and resource-intensive, particularly with large datasets. Additionally, GBMs are prone to overfitting, especially when the model is too complex or the learning rate is set too high.

However, these challenges can be mitigated with proper tuning and cross-validation. By carefully adjusting hyperparameters and using techniques like early stopping, you can prevent overfitting and maintain the model’s generalizability.

---

Learning Rate vs. Number of Trees

---

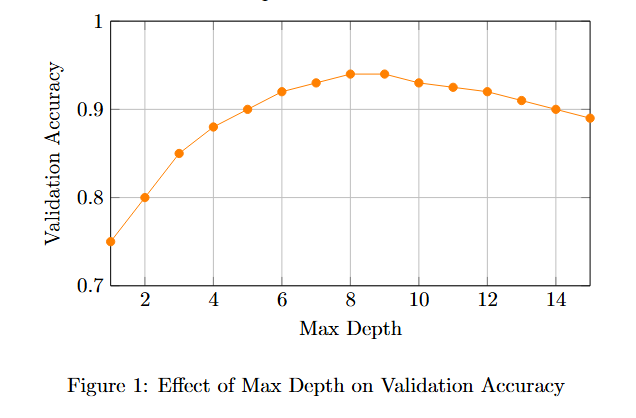
Max Depth vs. Model Performance

Comparing Random Forests and Gradient Boosting

When comparing Random Forests and Gradient Boosting Machines, it’s important to understand the trade-offs. Random Forests are generally easier to implement and faster to train, making them a good choice for quick, reliable results. They also require less tuning, which can be advantageous in situations where computational resources are limited or when you need a straightforward solution.

On the other hand, Gradient Boosting Machines offer superior performance in terms of accuracy and predictive power, especially when dealing with complex datasets. They require more expertise to tune but can yield significantly better results when used correctly.

The Role of Hyperparameter Tuning

The performance of a Gradient Boosting Machine heavily depends on how well it is tuned. Key hyperparameters include the learning rate, number of boosting rounds (or trees), and the maximum depth of each tree. The learning rate controls how much each tree contributes to the overall model, with smaller rates leading to more robust models that require more iterations. The number of boosting rounds determines how many trees are used, and the maximum depth controls the complexity of each tree.

Proper tuning requires a balance between these parameters. A smaller learning rate generally means a larger number of trees is needed, but this can lead to longer training times. Finding the right combination through techniques like grid search or random search can significantly enhance the model’s performance.

Handling Imbalanced Data

One area where Gradient Boosting Machines excel is in handling imbalanced datasets. In situations where certain classes are underrepresented, standard algorithms might struggle to make accurate predictions. GBMs, however, can be adjusted to give more weight to the minority class during training, thereby improving their ability to detect rare events. This feature is particularly valuable in fields like fraud detection or disease outbreak prediction, where identifying the minority class is crucial.

Regularization Techniques in GBMs

To combat overfitting, Gradient Boosting Machines incorporate several regularization techniques. These include shrinkage (where each tree’s contribution is scaled down), subsampling (training on a random subset of data), and penalizing tree complexity (limiting tree depth or the number of leaf nodes). These regularization methods help ensure that the model generalizes well to new data, rather than just memorizing the training set.

---

The Importance of Learning Rate

One of the most crucial hyperparameters in Gradient Boosting is the learning rate. A lower learning rate makes the model more cautious in its learning process, often leading to better generalization. However, this comes at the cost of needing more trees (or boosting rounds) to achieve the same level of accuracy.

Best Practice: Start with a low learning rate (e.g., 0.01 or 0.1) and gradually increase the number of trees to compensate. A common approach is to use grid search to find the optimal balance between the learning rate and the number of trees.

Balancing Number of Trees and Model Complexity

The number of trees is directly related to the model’s capacity to learn from data. While more trees generally lead to higher accuracy, too many trees can cause the model to overfit, especially if combined with a low learning rate.

Best Practice: Use cross-validation to determine the optimal number of trees. Implement early stopping, which halts the training process when no significant improvement is seen in a validation set after a set number of iterations. This technique not only saves time but also helps prevent overfitting.

Fine-Tuning Max Depth

The max depth of trees is another critical hyperparameter. Shallow trees might underfit by not capturing the complexity of the data, while deep trees may overfit by capturing too much noise.

Best Practice: Experiment with max depths between 3 and 10, depending on the complexity of the problem. Start with a lower value and gradually increase it until you see diminishing returns in accuracy or cross-validation scores.

Leveraging Subsampling for Robustness

Subsampling introduces randomness by using only a subset of the training data to fit each tree. This randomness can make the model more robust and prevent overfitting.

Best Practice: Use a subsample ratio between 0.5 and 1.0. Lower values add more randomness, which can be beneficial for noisy datasets. However, too low a value may reduce the model’s ability to learn from the data effectively.

Optimizing Min Samples Split and Min Samples Leaf

The min samples split and min samples leaf parameters control how the tree splits data and what constitutes a leaf node. These parameters directly affect the complexity of the model.

Best Practice: Start with default values and increase them gradually. Higher values for min samples split and min samples leaf encourage the model to make splits only when there’s sufficient data, thus reducing overfitting.

Regularization Techniques

Regularization helps to prevent overfitting by penalizing the model’s complexity. L1 (alpha) regularization encourages sparsity (useful when dealing with high-dimensional data), while L2 (lambda) regularization penalizes large coefficients more generally.

Best Practice: Regularization should be used sparingly. Start with small values (e.g., 0.01 for alpha and lambda) and increase only if you notice overfitting. These parameters can be fine-tuned using cross-validation to find the sweet spot where the model is neither too simple nor too complex.

Cross-Validation: Your Best Friend in Tuning

Cross-validation is indispensable when tuning Gradient Boosting Machines. By dividing your dataset into multiple folds and training the model on different subsets, you can better gauge how well your model will perform on unseen data.

Best Practice: Use k-fold cross-validation with a large enough k (typically 5 or 10) to ensure a reliable estimate of model performance. Combine cross-validation with grid search or random search to efficiently explore the hyperparameter space.

Grid Search vs. Random Search

When tuning multiple hyperparameters, it’s important to choose the right search strategy. Grid search exhaustively searches through a specified parameter grid, while random search samples from a specified distribution of hyperparameter values.

Best Practice: If you have a limited budget for computation, random search can be more efficient since it explores the hyperparameter space more broadly. For more fine-tuned control, especially when you have fewer hyperparameters to optimize, grid search might be more appropriate.

The Role of Feature Engineering

Although not a hyperparameter, feature engineering plays a crucial role in the success of a Gradient Boosting Machine. The quality of the features fed into the model significantly affects its performance.

Best Practice: Spend time understanding your data and engineering features that capture the underlying patterns more effectively. Techniques such as creating interaction terms, binning continuous variables, and handling missing values can enhance the model’s ability to learn.

Iteration is Key

Tuning a Gradient Boosting Machine is an iterative process. It requires careful adjustment of hyperparameters, guided by cross-validation and domain knowledge. By following these best practices—starting with a low learning rate, balancing the number of trees and max depth, leveraging subsampling, and applying regularization—you can significantly improve the performance of your GBM model.

Remember, the goal is to achieve a model that generalizes well to unseen data. Proper tuning of hyperparameters will get you there, but it’s the combination of good data, effective feature engineering, and iterative optimization that will make your model truly shine.

The Future of Gradient Boosting

The continued development of Gradient Boosting Machines suggests they will remain a cornerstone of machine learning for years to come. Innovations such as XGBoost, LightGBM, and CatBoost have made gradient boosting even more accessible and efficient, with faster training times and improved handling of categorical features. As these algorithms evolve, we can expect even greater performance and applicability across diverse domains.

Conclusion

While Random Forests remain a reliable and popular choice in machine learning, Gradient Boosting Machines offer a level of precision and adaptability that often makes them the superior option. Their ability to iteratively refine predictions, handle complex datasets, and manage imbalances makes them indispensable in many high-stakes applications. With ongoing advancements in gradient boosting technology, the future looks bright for this powerful algorithm.

For further reading and more detailed explorations of Gradient Boosting and its applications, check out these resources:
Gradient Boosting in Machine Learning
XGBoost Documentation
LightGBM Overview
CatBoost Features